Introduction
.
The Vertex Cover Problem is a well-known problem in computer science and graph theory.
This problem is important in the study of NP-completeness because it is one of the NP-complete problems. This means that no fast (polynomial-time) solution is known for it, and it is as hard as any problem in the NP class.
But there is a riddle which you have to solve to understand vertex cover problem.
.
Riddle –
I am a network of roads between towns,
You need to watch each road, ups and downs.
But cameras are costly, and you must be wise,
To cover each road with the smallest prize.
One camera at each town you place,
But not every town—just a few in space.
What is the smallest group, can you guess,
That covers all roads with no road left to stress?
.

.
Imagine you are designing a city surveillance system where you want to monitor all the streets. Instead of placing a 360-degree camera at every single intersection, you only place 360-degrees cameras at selected intersections (towns) so that every street (road) is watched by at least one camera. Your goal is to use the fewest cameras while still covering all the streets. How do you decide where to place them?
This riddle relates to the Vertex Cover Problem—find the smallest set of intersections (vertices) where 360-degree cameras should be placed to monitor all roads (edges).
.
History
The problem was first formally studied in the context of graph theory in the early 1970s. The problem is linked to various practical applications, such as network security, resource allocation, and scheduling.
In 1972, Stephen Cook introduced the concept of NP-completeness in his seminal paper on the P vs NP problem. The Vertex Cover problem was one of the first problems to be proven NP-complete, making it a fundamental problem in the study of computational complexity.
.
Problem Statement – (2-Approximation Algorithm)
Given an undirected graph G = (V, E), where V is the set of vertices and E is the set of edges, the task is to find a subset of vertices C ⊆ V such that every edge in the graph is incident to at least one vertex in C.
The objective is to minimize the size of this subset.
However, finding the smallest possible vertex cover is an NP-hard problem, making it computationally infeasible for large graphs. To address this, a 2-approximation algorithm is used, which efficiently finds a vertex cover that is at most twice the size of the optimal solution.
.
.
Why there is 2 in 2-Approximation Algorithm?
The “2” in the term 2-approximation algorithm refers to the approximation ratio or the guaranteed bound of the algorithm. This means the solution provided by the algorithm is at most twice (2 times) the size of the optimal solution.
Using the 2-approximation algorithm, find a vertex cover C such that ∣C∣ ≤ 2⋅∣COPT∣
where ∣COPT∣ is the size of the optimal (smallest) vertex cover.
This ensures that the solution is at most twice the size of the optimal solution while maintaining computational efficiency.
.
Algorithm of Vertex Cover
- Initialize an empty set C to store the vertex cover.
- While there are edges remaining in E
- Select any edge (u, v) from E.
- Add both u and v to C.
- Remove all edges from E that are incident to u or v.
- Output the set C as the vertex cover.
.
Example –
We are given a graph, and we need to find the set of vertices (nodes) such that every edge in the graph is covered. This means that for each edge, at least one of its two endpoints (vertices) must be included in the vertex cover.
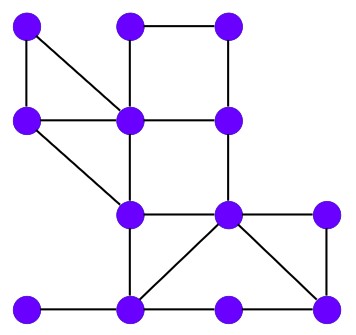
Step 1 – Initialize an empty set C to store the vertex cover.
C = { }
Step 2 – While there are edges in the graph
- Select any edge (u, v) from E
- Add both u and v to C.
- Remove all edges from E that are incident to u or v.
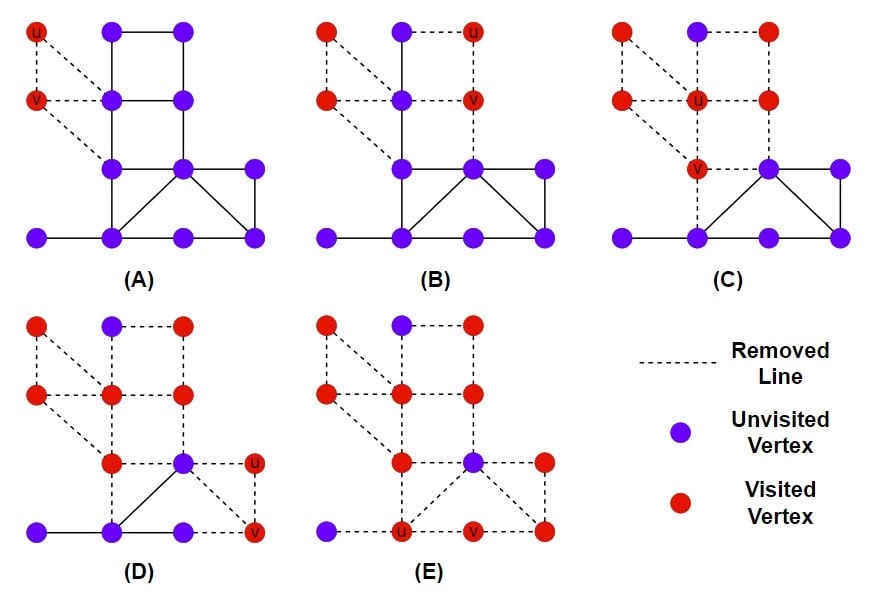
.
You can see in diagram (A), we have taken an edge and the two end vertices are u and v. The red colour vertex is the visited vertex. We have removed all edges related to u and v in (A) case.
In (B), (C), (D) and (E), we introduced new u and v vertex, colour them red and remove all edges related to u and v. In (E), we have covered all the edges.
In this approximation algorithm, we have a Vertex Cover = 10.
.
Although this selection of red vertices successfully covers all the edges, it might not represent the minimal set required to cover every edge. This solution provides a valid but potentially non-optimal vertex cover.
To achieve the minimal vertex cover, we can apply a heuristic algorithm that focuses on the degree of the vertices.
- Identify the vertex with the highest degree (the one connected to the most edges).
- Add this vertex to the vertex cover because it will cover the most edges at once.
- Remove all the edges connected to this vertex (since they are now covered).
- Repeat the process with the remaining vertices until all edges are covered.
Green edges are removed Edges
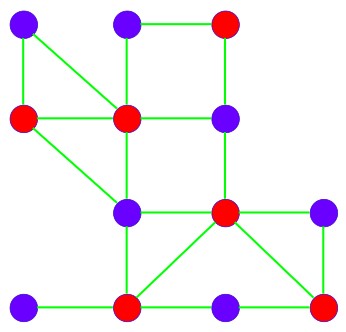
.
In the heuristic algorithm, we have a Vertex Cover = 6
This approach helps minimize the number of vertices selected for the cover. Though it may not always give the absolute minimal cover (as it’s a heuristic), it often provides a close-to-optimal solution.
This means if the optimal solution has a vertex cover of size 6, the algorithm will find a vertex cover of size at most 2 × 6 = 12.
In the example we discussed, the algorithm gave us a vertex cover of size 10, which satisfies the approximation bound, 10 ≤ 2×6.
.
Source Code for Vertex Cover Problem
// COMPUTER GEEK – compgeek.co.in
// Write a program for Vertex Cover Problem using
// 2-approximation algorithm
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTICES 100
// Structure to represent the graph
typedef struct {
int adj[MAX_VERTICES][MAX_VERTICES]; // Adjacency matrix
int num_vertices;
} Graph;
// Function to initialize the graph
void init_graph(Graph* g, int vertices) {
g->num_vertices = vertices;
for (int i = 0; i < vertices; i++) {
for (int j = 0; j < vertices; j++) {
g->adj[i][j] = 0; // No edge initially
}
}
}
// Function to add an edge to the graph
void add_edge(Graph* g, int u, int v) {
g->adj[u][v] = 1;
g->adj[v][u] = 1; // As it’s an undirected graph
}
// Function to perform the 2-approximation algorithm
void vertex_cover_2_approx(Graph* g) {
int covered[MAX_VERTICES] = {0}; // Track covered vertices
int vertex_cover[MAX_VERTICES] = {0}; // Store vertex cover
int cover_size = 0;
// Iterate while there are edges
for (int u = 0; u < g->num_vertices; u++) {
for (int v = u + 1; v < g->num_vertices; v++) {
if (g->adj[u][v] == 1 && !covered[u] && !covered[v]) {
// Add both vertices to the vertex cover
vertex_cover[cover_size++] = u;
vertex_cover[cover_size++] = v;
covered[u] = 1;
covered[v] = 1;
// Remove all edges incident to u and v
for (int i = 0; i < g->num_vertices; i++) {
g->adj[u][i] = 0;
g->adj[i][u] = 0;
g->adj[v][i] = 0;
g->adj[i][v] = 0;
}
break; // Move to the next edge
}
}
}
// Output the vertex cover
printf(“Vertex Cover: “);
for (int i = 0; i < cover_size; i++) {
printf(“%d “, vertex_cover[i]);
}
printf(“\n”);
}
int main() {
Graph g;
int vertices, edges;
int u, v;
// Take input for the graph
printf(“Enter the number of vertices: “);
scanf(“%d”, &vertices);
init_graph(&g, vertices);
printf(“Enter the number of edges: “);
scanf(“%d”, &edges);
// Take the edges as input
for (int i = 0; i < edges; i++) {
printf(“Enter edge %d (u v): “, i + 1);
scanf(“%d %d”, &u, &v);
add_edge(&g, u, v);
}
// Run the 2-approximation algorithm for vertex cover
vertex_cover_2_approx(&g);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Vertex Cover Problem using
// 2-approximation algorithm
#include <iostream>
#include <vector>
using namespace std;
class Graph {
public:
vector<vector<int>> adj;
int num_vertices;
Graph(int vertices) {
num_vertices = vertices;
adj.resize(vertices, vector<int>(vertices, 0));
}
void addEdge(int u, int v) {
adj[u][v] = 1;
adj[v][u] = 1;
}
void vertexCover2Approx() {
vector<bool> covered(num_vertices, false);
vector<int> vertex_cover;
for (int u = 0; u < num_vertices; u++) {
for (int v = u + 1; v < num_vertices; v++) {
if (adj[u][v] == 1 && !covered[u] && !covered[v]) {
vertex_cover.push_back(u);
vertex_cover.push_back(v);
covered[u] = true;
covered[v] = true;
for (int i = 0; i < num_vertices; i++) {
adj[u][i] = 0;
adj[i][u] = 0;
adj[v][i] = 0;
adj[i][v] = 0;
}
break;
}
}
}
// Output the vertex cover
cout << “Vertex Cover: “;
for (int i : vertex_cover) {
cout << i << ” “;
}
cout << endl;
}
};
int main() {
int vertices, edges;
cout << “Enter the number of vertices: “;
cin >> vertices;
Graph g(vertices);
cout << “Enter the number of edges: “;
cin >> edges;
for (int i = 0; i < edges; i++) {
int u, v;
cout << “Enter edge ” << i + 1 << ” (u v): “;
cin >> u >> v;
g.addEdge(u, v);
}
g.vertexCover2Approx();
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Vertex Cover Problem using
// 2-approximation algorithm
import java.util.*;
class Graph {
int numVertices;
int[][] adj;
public Graph(int vertices) {
numVertices = vertices;
adj = new int[vertices][vertices];
}
public void addEdge(int u, int v) {
adj[u][v] = 1;
adj[v][u] = 1;
}
public void vertexCover2Approx() {
boolean[] covered = new boolean[numVertices];
ArrayList<Integer> vertexCover = new ArrayList<>();
for (int u = 0; u < numVertices; u++) {
for (int v = u + 1; v < numVertices; v++) {
if (adj[u][v] == 1 && !covered[u] && !covered[v]) {
vertexCover.add(u);
vertexCover.add(v);
covered[u] = true;
covered[v] = true;
for (int i = 0; i < numVertices; i++) {
adj[u][i] = 0;
adj[i][u] = 0;
adj[v][i] = 0;
adj[i][v] = 0;
}
break;
}
}
}
// Output the vertex cover
System.out.print(“Vertex Cover: “);
for (int i : vertexCover) {
System.out.print(i + ” “);
}
System.out.println();
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.print(“Enter the number of vertices: “);
int vertices = sc.nextInt();
Graph g = new Graph(vertices);
System.out.print(“Enter the number of edges: “);
int edges = sc.nextInt();
for (int i = 0; i < edges; i++) {
System.out.print(“Enter edge ” + (i + 1) + ” (u v): “);
int u = sc.nextInt();
int v = sc.nextInt();
g.addEdge(u, v);
}
g.vertexCover2Approx();
sc.close();
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for Vertex Cover Problem using
# 2-approximation algorithm
class Graph:
def __init__(self, vertices):
self.num_vertices = vertices
self.adj = [[0] * vertices for _ in range(vertices)]
def add_edge(self, u, v):
self.adj[u][v] = 1
self.adj[v][u] = 1
def vertex_cover_2_approx(self):
covered = [False] * self.num_vertices
vertex_cover = []
for u in range(self.num_vertices):
for v in range(u + 1, self.num_vertices):
if self.adj[u][v] == 1 and not covered[u] and not covered[v]:
vertex_cover.append(u)
vertex_cover.append(v)
covered[u] = True
covered[v] = True
for i in range(self.num_vertices):
self.adj[u][i] = 0
self.adj[i][u] = 0
self.adj[v][i] = 0
self.adj[i][v] = 0
break
# Output the vertex cover
print(“Vertex Cover:”, ” “.join(map(str, vertex_cover)))
def main():
vertices = int(input(“Enter the number of vertices: “))
g = Graph(vertices)
edges = int(input(“Enter the number of edges: “))
for i in range(edges):
u, v = map(int, input(f”Enter edge {i + 1} (u v): “).split())
g.add_edge(u, v)
g.vertex_cover_2_approx()
if __name__ == “__main__”:
main()
Enter the number of vertices: 6
Enter the number of edges: 6
Enter edge 1 (u v): 0 1
Enter edge 2 (u v): 1 2
Enter edge 3 (u v): 2 3
Enter edge 4 (u v): 3 4
Enter edge 5 (u v): 4 5
Enter edge 6 (u v): 0 5
Vertex Cover: 0 1 2 3 4 5
=== Code Execution Successful ===
Time Complexity
In the worst case, we have to consider each edge of the graph. For each edge, look at vertices, mark as covered, and subtract their connected edges. This has a time complexity of O(V).
Since the edges are up to E in number, the overall time is O(E*V), with E the edges and V the number of vertices.
.
Space Complexity
The graph employs a matrix to keep track of edges, which consumes O(V2) space. The covered array consumes O(V) space and the vertex cover list consumes at most O(V) space.
Therefore, the space complexity is O(V2).
This is because it uses an adjacency matrix in representing the graph. However, reducing the space complexity to O(V+E) is by using an adjacency list instead.
.
Applications
1. Network Design – The vertex cover problem can be applied in designing networks, such as communication networks or computer networks. In this case, the meaning of the vertex cover is selecting a subset of nodes to be covered or protected, and the edges represent the connections that require coverage.
2. Resource allocation – if some resources must be allocated in order to cope with interactions or connections between tasks or systems, then the vertex cover will find the least number of resources to handle all the dependencies.
3. Scheduling Problems – The vertex cover can determine which tasks should be scheduled or monitored so that all inter-task dependencies are considered when planning tasks that depend on one another.
4. Biological Networks – The vertex cover can be used in biological networks, such as protein-protein interaction networks, to find the smallest set of proteins forming part of interactions.
Test Yourself
Q1- Why is the Vertex Cover Problem classified as NP-complete?
The Vertex Cover Problem is NP-complete because verifying a given solution is possible in polynomial time, but no polynomial-time algorithm is known to solve all instances of the problem.
Q2- What is a 2-approximation algorithm, and why is it used for the Vertex Cover Problem?
A 2-approximation algorithm finds a vertex cover within twice the size of the optimal solution. It is used because finding the exact solution is computationally infeasible for large graphs.
Q3- Describe the heuristic method for finding a minimal vertex cover.
The heuristic method selects the vertex with the highest degree, adds it to the vertex cover, and removes all edges incident to it. This process repeats until all edges are covered. The vertex degree indicates the number of edges connected to a vertex. Selecting high-degree vertices first ensures more edges are covered with fewer vertices.
Q4- Provide a real-world application of the Vertex Cover Problem.
A real-world application is in network security, where 360 degrees cameras must be placed at intersections (vertices) to monitor all roads (edges).
Q5- Is it possible for the 2-Approximation Algorithm to include all vertices of the graph in the vertex cover? Under what circumstances?
Yes, in a complete graph Kn, where n is even. The algorithm includes all vertices since every edge connects every pair of vertices.
Q6- What is the goal of the Vertex Cover Problem?
Find the largest set of vertices
Find the smallest set of vertices
Find the longest path in the graph
Find the shortest path in the graph
Ans – (2)
Explanation – The goal is to find the smallest set of vertices that covers all edges.
Q7- What is the approximation ratio of the 2-approximation algorithm for Vertex Cover?
1
1.5
2
3
Ans – (3)
Explanation – The solution is guaranteed to be at most twice the size of the optimal solution.
Q8- In the 2-approximation algorithm, how many vertices are added for each selected edge?
1
2
3
4
Ans – (2)
Explanation – Both endpoints of the selected edge are added to the vertex cover.
Q9- Which of the following graphs has the smallest vertex cover size?
Complete graph
Tree
Bipartite graph
Cycle graph
Ans – (2)
Explanation – In a tree, a minimal vertex cover includes all parent vertices, which is fewer than in other graph types.
Q10- What type of graph structure leads to the largest vertex cover size?
Complete graph
Tree
Sparse graph
Bipartite graph
Ans – (1)
Explanation – In a complete graph, all vertices may be required to cover edges, leading to the largest vertex cover.






