Vertex Cover Problem

Introduction

.

The Vertex Cover Problem is a well-known problem in computer science and graph theory.

This problem is important in the study of NP-completeness because it is one of the NP-complete problems. This means that no fast (polynomial-time) solution is known for it, and it is as hard as any problem in the NP class.

However, there’s a riddle that you need to solve to grasp the concept of the vertex cover problem.

.

Riddle

I am a network of roads between towns,
You need to watch each road, ups and downs.
But cameras are costly, and you must be wise,
To cover each road with the smallest prize.

One camera at each town you place,
But not every town—just a few in space.
What is the smallest group, can you guess,
That covers all roads with no road left to stress?

.

Imagine you are designing a city surveillance system where you want to monitor all the streets. Instead of placing a 360-degree camera at every single intersection, you only place 360-degrees cameras at selected intersections (towns) so that every street (road) is watched by at least one camera. Your goal is to use the fewest cameras while still covering all the streets. How do you decide where to place them?

This riddle relates to the Vertex Cover Problem—find the smallest set of intersections (vertices) where 360-degree cameras should be placed to monitor all roads (edges).

.

Example –

We are given a graph, and we need to find the set of vertices (nodes) such that every edge in the graph is covered. This means that for each edge, at least one of its two endpoints (vertices) must be included in the vertex cover.

.

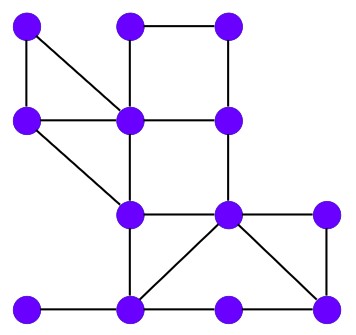
The solution was created by an inexperienced student who attempted to solve the Vertex Cover Problem. The student selected the red vertices, ensuring that all edges (shown in green) are covered, as each edge is connected to at least one red vertex.

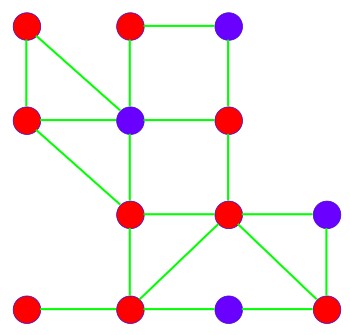
Vertex Cover = 9

.

Although this selection of red vertices successfully covers all the edges, it might not represent the minimal set required to cover every edge. This solution provides a valid but potentially non-optimal vertex cover.

To achieve the minimal vertex cover, we can apply a heuristic algorithm that focuses on the degree of the vertices.

1. Identify the vertex with the highest degree (the one connected to the most edges).
2. Add this vertex to the vertex cover because it will cover the most edges at once.
3. Remove all the edges connected to this vertex (since they are now covered).
4. Repeat the process with the remaining vertices until all edges are covered.

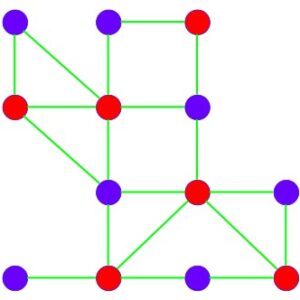
Vertex Cover = 6

.

This approach helps minimize the number of vertices selected for the cover. Though it may not always give the absolute minimal cover (as it’s a heuristic), it often provides a close-to-optimal solution.

.

The Vertex Cover Problem can be divided into two types

1. Minimal Vertex Cover Problem – Find the smallest vertex cover.
2. Weighted Vertex Cover – Find the vertex cover with the smallest total weight.
3. The Decision Problem of determining whether a graph has a vertex cover, by selecting at most k vertices.

.

Vertex Cover Optimization Problem

The Vertex Cover Optimization Problem is a fundamental problem in graph theory and computer science. The goal of this problem is to find the smallest possible set of vertices (called the vertex cover) that covers all the edges in a given graph. The Minimal Vertex Cover Problem and Weighted Vertex Cover are the optimization problem.

Can you find the minimal vertex cover in the below graph?

.

Not in the polynomial time, because it is a very very hard problem. We can follow any methodology like brute force algorithm, greedy algorithm, approximation algorithm or parameterized algorithm, we can never make the time complexity less than exponential. So, this optimization problem is NP-Hard.

.

Vertex Cover Decision Problem

The Vertex Cover Decision Problem is a variant of the vertex cover problem that asks whether a vertex cover of a specified size exists for a given graph. In simpler terms, the decision problem asks, “Can we cover all the edges in this graph by selecting at most k vertices?”

.

History

The problem was first formally studied in the context of graph theory in the early 1970s. The problem is linked to various practical applications, such as network security, resource allocation, and scheduling.

In 1972, Stephen Cook introduced the concept of NP-completeness in his seminal paper on the P vs NP problem. The Vertex Cover problem was one of the first problems to be proven NP-complete, making it a fundamental problem in the study of computational complexity.

The decision version of the Vertex Cover problem was among the 21 NP-complete problems identified by Richard Karp and is considered a fundamental NP-complete problem in the field of computational complexity theory.

.

Proof of Vertex Cover Decision Problem is NP-Complete

One common approach is to reduce from the 3-SAT problem.

The key idea is to construct a graph from a 3-SAT instance in such a way that there is a vertex cover of size k in the graph if and only if the 3-SAT instance is satisfiable. The construction generally involves creating vertices for variables and their negations, and additional vertices for clauses.

If we can transform an instance of 3-SAT to an instance of Vertex Cover in polynomial time, and if solving Vertex Cover would allow us to solve 3-SAT, then Vertex Cover is NP-complete.

.

Algorithm 3-SAT_to_VertexCover

1. Create an empty graph G and initialize an empty set of vertices.
2. For each variable x_i, add two vertices x_i and ¬x_i and put an edge between the two.
3. Create three vertices C_j1, C_j2, C_j3 representing the three literals in the clause C_j.
4. Connect the three clause vertices to form a triangle.
5. Set vertex cover size k = 2C + X, where X is the number of variables and C is the number of clauses.
6. Return the graph G and the integer k.

.

Example –

Consider the formula

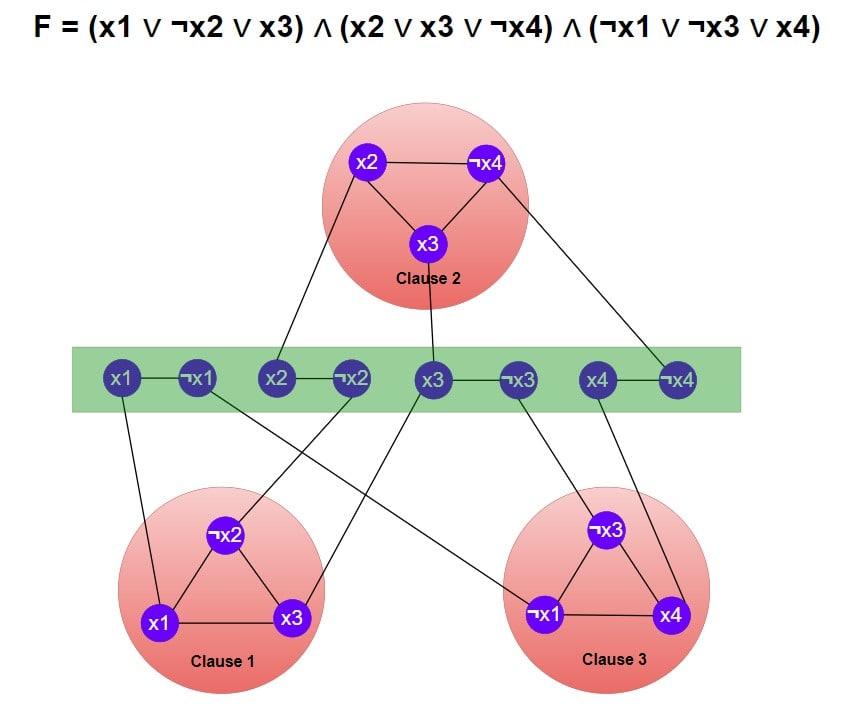
F = (x1 ∨ ¬x2 ∨ x3) ∧ (x2 ∨ x3 ∨ ¬x4) ∧ (¬x1 ∨ ¬x3 ∨ x4)

Step 1 – Create a graph and for each variable x_i, add two vertices x_i and ¬x_i and put an edge between the two. It is showing in green colour rectangle.

.

Step 2 – Create three vertices C_j1, C_j2, C_j3 representing the three literals in the clause C_j. Connect the three clause vertices to form a triangle. This is shown by pink circles.

Step 3 – Set vertex cover size k = 2C + X, where X is the number of variables and C is the number of clauses.

Vertex cover size k = 2(3) + 4 = 10.

We need to find a minimum vertex cover with exactly 10 vertices to ensure that every edge in the graph is connected to at least one vertex in the vertex cover.

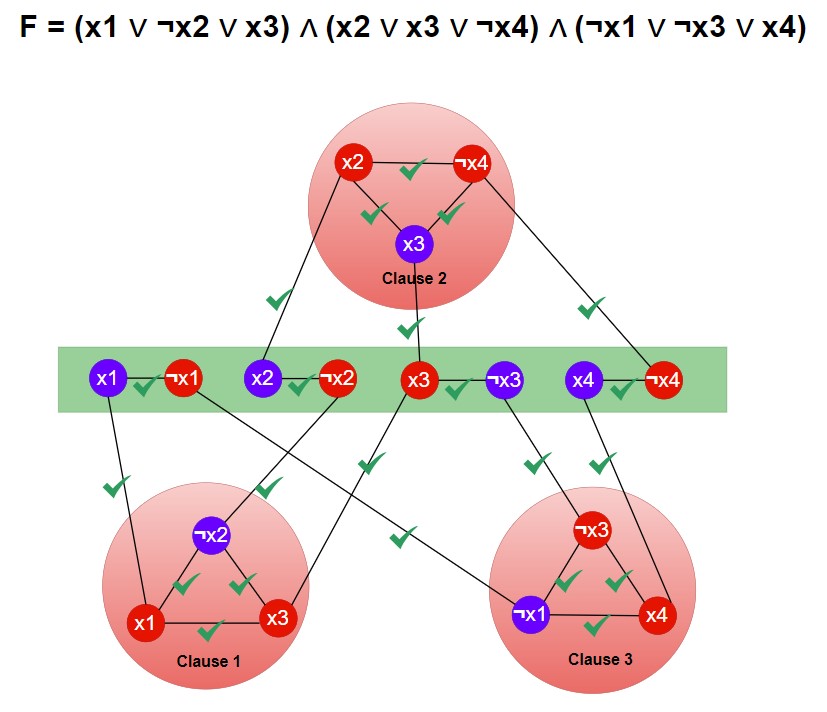
We solved this problem

.

Every edge in the graph is connected to at least one vertex in the vertex cover. Number of Vertex Cover = 10 Vertices.

So, we have proved that 3-SAT is NP-Complete. We know that vertex cover problem NP, so we have also proved that by reduction of 3-SAT to Vertex Cover in polynomial time, that vertex cover problem is also NP-Complete.

If we can say that 3-SAT can be reduced to Vertex Cover Problem, it means that solving Vertex Cover Problem would allow us to solve 3-SAT as well.

Let’s verify from the above example. The vertex problem is solved and we need to solve 3-SAT problem by the vertices of vertex cover.

By seeing the x_i and ¬x_i in the green colour, the vertex in red colour decides true or false of the variable.

In the diagram, red colour

¬x1 represents x1 = false,

¬x2 represents x2 = false,

x3 represents x3 = true and

¬x4 represents x4 = false.

F = (x1 ∨ ¬x2 ∨ x3) ∧ (x2 ∨ x3 ∨ ¬x4) ∧ (¬x1 ∨ ¬x3 ∨ x4)

F = (False V True V True) ∧ (True V True V True) ∧ (True V False V False)

F = True ∧ True ∧ True

F = True

Hence, 3-SAT Problem is true. it means that solving Vertex Cover Problem would allow us to solve 3-SAT as well.