Q1 – Which of the following are tautology?
A. (P → (P Λ Q)) → (P → Q)
B. ((P → Q) → Q) → (P V Q)
C. ((P V ¬P) → Q) → (P V ¬P) → R)
D. (Q → (P Λ ¬P)) → (R → (P Λ ¬P))
A only
B only
A and B only
C and D only
Ans – (3)
Explanation –
A. (P → (P Λ Q)) → (P → Q)
- (¬ P v (P ∧ Q)) → (P → Q)
- (¬ P v P ∧ ¬ P v Q) → (P → Q)
- (¬ P v Q) → (P → Q)
- (¬ P v Q) → (¬ P v Q)
If x → x, then it’s a tautology.
.
B. ((P → Q) → Q) → (P V Q)
- ((¬ P v Q) → Q) → (P ∨ Q)
- (¬ (¬ P v Q) v Q) → (P ∨ Q)
- (P ∧ ¬ Q) v Q) → (P ∨ Q)
- (P v Q ∧ ¬ Q v Q) → (P ∨ Q)
- (P v Q) → (P ∨ Q)
If x → x, then it’s a tautology
Alternative way
A.
P | Q | PΛQ | P→Q | P→(PΛQ) | (P→(PΛQ)) → (P→Q) |
0 | 0 | 0 | 1 | 1 | 1 |
0 | 1 | 0 | 1 | 1 | 1 |
1 | 0 | 0 | 0 | 0 | 1 |
1 | 1 | 1 | 1 | 1 | 1 |
B.
P | Q | P→Q | (P→Q)→Q | PVQ | ((P→Q)→Q) → (PVQ) |
0 | 0 | 1 | 0 | 0 | 1 |
0 | 1 | 1 | 1 | 1 | 1 |
1 | 0 | 0 | 1 | 1 | 1 |
1 | 1 | 1 | 1 | 1 | 1 |
Q2 – Arrange the following in ascending order
(a) Remainder of 4916 when divided by 17
(b) Remainder of 2446 when divided by 9
(c) Remainder of 15517 when divided by 17
(d) Last digit of the number 745
Choose the correct answer from the options given below
(a), (b), (c), (d)
(a), (b), (d), (c)
(a), (c), (b), (d)
(d), (c), (b), (a)
Ans – (3)
Explanation – (a): 4916 = (51 – 2)16
Since 51 is divisible by 17, its remainder when divided by 17 will be (-2)16
(-2)16 = (-2)4*4 = (16)4 = (17 – 1)4
Since 17 is divisible by 17, its remainder when divided by 17 will be (-1)4 = 1
(b): 2446
21 = 2 mod 9 = 2
22 = 4 mod 9 = 4
23 = 8 mod 9 = 8
24 = 16 mod 9 = 7
25 = 32 mod 9 = 5
26 = 64 mod 9 = 1
We can see that 2n mod 9 repeats every 6 terms, 2, 4, 8, 7, 5, 1
You can check 27 = 128 mod 9 = 2
So, the cycle repeats every 6 terms, then we can reduce 446 mod 6. So, 446 mod 6 = 2.
In the cycle of 2, 4, 8, 7, 5, 1, the 2nd term which is 4 is our remainder.
(c): 15517 = (153 + 2)17
Since 153 is divisible by 17, its remainder when divided by 17 will be 217 = 2*216
216 = 24*4 = 164 = (17 – 1)4
Since 17 is divisible by 17, its remainder when divided by 17 will be (-1)4 = 1
Then the overall remainder is 2*216 = 2*1 = 2
(d): 745
71 = 7
72 = 49
73 = 343
74 = 2401
So, the last digit repeats every 4 terms. 7, 9, 3, 1
We can reduce 45 by 45 mod 4 = 1
In the cycle of 7, 9, 3, 1, the 1st term which is 7 is our remainder.
By sorting the options in ascending order remainders, we get option 3. (a), (c), (b), (d)
Q3 – Given below are two statements:
Statement I – If H is non empty finite subset of a group G and ab ϵ H ꓯ a, b ϵ H, then H is also a group.
Statement II – There is no homomorphism exist from (Z, +) to (Q, +); where Z is set of integers and Q is set of rational number.
In the light of the above statements, choose the most appropriate answer from the options given below:
Both Statement I and Statement II are correct.
Both Statement I and Statement II are incorrect.
Statement I is correct, but Statement II is incorrect.
Statement I is incorrect, but Statement II is correct.
Ans – (3)
Explanation – Statement I discusses subgroups in the theory of groups.
A group is defined as a set that possesses a binary operation-and-satisfies four properties
Closure – If a and b belong to the group, then ab is also a member of the group.
Identity – There exists an element e such that ae = ea = a for all a.
Inverse – For every a, there exists an a−1 such that aa−1=e.
Associativity – (ab)c = a(bc).
Now, if H is a nonempty finite subset of G, the condition states that multiplying any two elements from H results in still another member of H. This condition is, hence, called closure. So, statement I is true.
Statement II is about some homomorphisms between two mathematical structures.
A homomorphism is a function respecting the group operation. If f: (Z,+) → (Q,+) is a homomorphism, then it must satisfy
f(a+b) = f(a) + f(b) ∀a,b ∈ Z.
The question itself says no such function exists. Thus, there is no possible mapping of the integers into the rational numbers that preserves addition. But this is false, for a simple homomorphism is f(n)=n. Hence Statement II is false.
Q4 – If universe of disclosure are all real numbers, then which of the following are true?
(a) ꓱx ꓯy (x + y = y)
(b) ꓯx ꓯy(((x ≥ 0) Λ (y < 0)) à (x – y > 0))
(c) ꓱx ꓱy(((x ≤ 0) Λ (y ≤ 0)) Λ (x – y > 0))
(d) ꓯx ꓯy(((x ≠ 0) Λ (y ≠ 0)) ↔ (xy ≠ 0))
Choose the correct answer from the options given below:
(a) and (b) only
(a), (c) and (d) only
(a), (c) and (d) only
(a), (b), (c) and (d) only
Ans – (4)
Explanation – ꓱx meaning is “there exist a number x”, and ꓯx meaning is “for all x”.
(a) – ꓱx ꓯy (x + y = y)
This means there exists some real number x, such that for all y, the equation x + y = y holds. When x = 0, then this option is true.
(b) – ꓯx ꓯy(((x ≥ 0) Λ (y < 0)) à (x – y > 0))
This means for all real numbers x and y, if x is non-negative and y is negative, then x – y > 0.
So, x – (-y) is always positive, hence this option is true.
(c) – ꓱx ꓱy(((x ≤ 0) Λ (y ≤ 0)) Λ (x – y > 0))
This means that there exist real numbers x and y such that if x is negative, and y is also negative, then x – y > 0
If we take x = – 2, y = -3, then (-2) – (-3) > 0
(d) – ꓯx ꓯy(((x ≠ 0) Λ (y ≠ 0)) ↔ (xy ≠ 0))
This means that for all x and y, if x is non-zero and y is non-zero then xy is non-zero and vice-versa.
Option 4 is correct.
Q5 – Match List-I with List-II
List-I(Propositions) | List-II(Disjunctive Normal Form (DNF)) |
(a) P Λ (P → Q) | I. P V Q |
(b) ¬(P V Q) → (P Λ Q) | II. (P Λ ¬P) V (P Λ Q) |
(c) P → Q | III. (¬P) V Q |
(d) P V (Q Λ R) | IV. (P Λ P) V (P Λ Q) V (P Λ R) V (Q Λ R) |
Choose the correct answer from the options given below
(a) | (b) | (c) | (d) | |
1. | I | II | III | IV |
2. | II | I | III | IV |
3. | III | I | II | IV |
4. | IV | III | II | I |
Ans – (2)
Explanation – (a) P Λ (P → Q)
=> P Λ (¬(P V Q))
=> (P Λ ¬P) V (P Λ Q) which is II.
(b) ¬(P V Q) → (P Λ Q)
=> ¬(¬(P V Q) V (P Λ Q))
=> ((P V Q) V ¬(P Λ Q))
=> ((P V Q) V (P V Q))
=> (P V Q), which is I.
(c) P → Q
=> ¬P V Q, which is III.
(d) P V (Q Λ R)
=> The single list-II option is IV. So, we will check the IV,
IV. (P Λ P) V (P Λ Q) V (P Λ R) V (Q Λ R)
=> P V (P Λ Q) V (P Λ R) V (Q Λ R) as [P Λ P = P]
=> P V (P Λ R) V (Q Λ R) as Absorption law
=> P V (Q Λ R) as Absorption law. Also, it is equal to (d).
Q6 – If the universe of disclosure is set of integers, then which of the followings are TRUE?
(a) ꓯn ꓱm (n2 < m)
(b) ꓱn ꓯm (n < m2)
(c) ꓱn ꓱm (nm = m)
(d) ꓱn ꓱm (n2 + m2 = 6)
(e) ꓱn ꓱm (n + m = 4 Λ n – m = 1)
Choose the correct answer from the options given below
(a), (b) and (c) only
(b) and (c) only
(c), (d) and (e) only
(c) and (e) only
Ans – (2)
Explanation – Universe of discourse – Set of Integers
(a) ꓯn ꓱm (n2 < m) – For every integer n, there exists an integer m, such that n2 < m.
Example – If n = 4, then n2 = 16. We can take m = 17 which satisfies 16 < 17. Therefore, it is correct.
(b) ꓱn ꓯm (n < m2) – There exists some integer n such that for every integer m, n < m2. This statement is true.
Example – Let n = -1, then for every integer m, this expression n<m2 is true.
Let’s say m = 0, then n < m2 → -1 < 0
Let’s say m = -1, then n < m2 → -1 < 1
Let’s say m = 1, then n < m2 → -1 < 1
Let’s say m = -2, then n < m2 → -1 < 4
(c) ꓱn ꓱm (nm = m) – There exist integers n and m such that nm = m.
Let’s say n = 1 and m = any integer, then nm is that “any integer”, which satisfies the equation. Hence this statement is correct.
(d) ꓱn ꓱm (n2 + m2 = 6) – There exist integers n and m such that n2 + m2 = 6.
This is not correct. Because on squaring the two integers, the difference is not 6.
(-2)2 = 4, (-1)2 = 1, 02 = 0, 12 = 1, 22 = 4, 32 = 9, 42 = 16, 52 = 25
There are not two integers, who’s on squaring, get the difference 6.
(e) ꓱn ꓱm (n + m = 4 Λ n – m = 1) – There exist integers n and m such that n + m = 4 AND n – m = 1.
So, we have to find n and m where n + m = 4 and also n – m = 1.
Solving the equation, we get n = 2.5 and m = 1.5, which are not the integer. So, this statement is incorrect.
Q7 – If N2 = N x N, N is set of natural numbers and R is relation on N2, s.t. R C N2 x N2 i.e. <x, y> R <u, v> ↔ xv = yu, then which of the following are TRUE?
(a) Reflexive
(b) Symmetric
(c) Transitive
(d) Asymmetric
Choose the correct answer from the options given below:
(a) and (b) only
(b) and (c) only
(a), (c) and (d) only
(a), (b) and (c) only
Ans – (4)
Explanation – N is the set of natural numbers, means 1, 2, 3, 4, …
R is a relation on N2 where, <x, y> R <u, v> if and only if xv = yu
(a) Reflexive – A relation R is reflexive if each pair is related to itself.
In our question, (x, y) R (u, v) iff xv = yu
For reflexivity <x, y> R <x, y> that means x.y = y.x
Since x = u and y = v, it means xv = yu
So, relation R is reflexive.
(b) Symmetric – A relation R is symmetric if (x, y)R(u, v) holds, then (u, v)R(x, y) holds.
(x, y)R(u, v) => xv = yu, and
(u, v)R(x, y) => uy = vx
It is same xv = vx = yu = uy
So, relation is symmetric.
(c) Transitive – A relation R is transitive if (x, y)R(u, v) holds, then (u, v)R(p, q) also must hold.
(x, y)R(u, v) => xv = yu
(u, v)R(p, q) => uq = vp
We have to prove xq = yp
- xv = yu
- (xv)*q = (yu)*q
- Also, uq = vp
- y*(uq) = y*(vp)
- xvq = yvp [v cancel from both sides]
- xq = yp
(d) Asymmetric – we proved that relation R is symmetric. So, R is not asymmetric.
Option 4 is the answer.
Q8 – The statement P(x): “ x=x2 “. If the universe of disclosure consists of integers, what are the following have truth values :
(A) P(0)
(B) P(1)
(C) P(2)
(D) Ǝx P(x)
(E) ∀x P(x)
Choose the correct answer from the options given below:
(A), (B) and (E) Only
(A), (B) and (C) Only
(A), (B) and (D) Only
(B), (C) and (D) Only
Ans – (3)
Explanation – P(x): x = x²
This means that x must be equal to its square (x²).
(A) P(0): 0 = 0² Correct
(B) P(1): 1 = 1² Correct
(C) P(2): 2 = 2² => 2 = 4 Incorrect
(D) There exists at least one x such that x = x². So, this is also correct
(E) For all x, x = x² Incorrect.
Option 3 is the answer.
Q9 – 
Choose the correct answer from the options given below
(A)-(1), (B)-(II), (C)-(III), (D)-(IV)
(A)-(II), (B)-(I), (C)-(III), (D)-(IV)
(A)-(II), (B)-(I), (C)-(IV), (D)-(III)
(A)-(I), (B)-(II), (C)-(IV), (D)-(III)
Ans – (4)
Explanation – (A) ϕ ∩ {ϕ} match with (1) ϕ
- The intersection of the empty set ϕ with {ϕ} means finding common elements.
- Since ϕ has no elements, the result is also an empty set.
(B) {ϕ} ∩ {ϕ} match with (II) {ϕ}
- Both sets are {ϕ}, so their intersection is {ϕ}.
(C) {ϕ, {ϕ}} – ϕ match with (IV) {ϕ, {ϕ}}
- The difference between {ϕ, {ϕ}} and ϕ (empty set) means removing nothing, as ϕ has no elements.
(D) ϕ ∪ {{ϕ}} match with (III) {{ϕ}}
- The union of an empty set and {{ϕ}} results in {{ϕ}} because the empty set contributes nothing.
Q10 – What is the probability that a positive integer selected at random from the set of positive integer not exceeding 100 is divisible by either 2 or 5?
10/5
3/5
2/5
1/5
Ans – (2)
Explanation – We count numbers divisible by 2, 5, and both 2 and 5.
Numbers divisible by 2 is, 100/2 = 50
Numbers divisible by 5 is, 100/5 = 20
Numbers divisible by 2 and 5 means 10 is, 100/10 = 10
Apply the inclusion – exclusion formula, we get
- N(2 V 5) = N(2) + N(5) – N(10)
- N(2 V 5) = 50 + 20 – 10
- N(2 V 5) = 60
- P(2 V 5) = 60/100 = 3/5.
Q11 – Which of the following statement are truth statements if universe of disclosure is set of integers:
(A) ∀n (n2 >= 0)
(B) ∃n (n2 = 2)
(C) ∀n (n2 >= n)
(D) ∃n (n2 < 0)
Choose the correct answer from the options given below :
(A) and (B) Only
(B) and (C) Only
(C) and (D) Only
(A) and (C) Only
Ans – (4)
Explanation – (A) ∀n (n2 >= 0) is true because for all integers, n2 >= 0,
If n = 0, then it is true
If n = 1, then it is true.
(B) ∃n (n2 = 2) is false because this means there exists an integer such that n2 = 2, which is not correct. Square of an integer is (0, 1, 4, 9, …)
(C) ∀n (n2 >= n) is true because this means that all integer square must be greater than or equal to that integer.
If n = 0, 0 >= 0, then it is true
If n = 1, 1 >= 1, then it is true.
If n = -1, 1 >= 1, then it is true.
If n = 2, 4 >= 2, then it is true.
(D) ∃n (n2 < 0) is false because this means there exists an integer such that n2 < 0.
If n = 0, 0 < 0 which is not true.
Question Number: 12-16
Question Label: Comprehension
Food X contains 6 units of Vitamin D per gram and 7 units of Vitamin E per gram and cost is Rs 12 per gram.
Food Y contains 8 units of vitamin D per gram and 12 units of Vitamin E per gram and cost is Rs 20 per gram.
The daily minimum requirements of vitamin D and E are 100 units and 120 units respectively.
Suppose x is quantity (in gram) of food X, y is quantity (in gram) of food Y. Answering the following question based on the above paragraph given.
Q12 – The minimum cost of food is :
205
250
330
200
Ans – (1)
Explanation – Food X contains
Vitamin D per gram = 6 units
Vitamin E per gram = 7 units
Cost = Rs 12 per gram
Food Y contains
Vitamin D per gram = 8 units
Vitamin E per gram = 12 units
Cost = Rs 20 per gram
Daily minimum requirement is
Vitamin D >= 100
Vitamin E >= 120
For vitamin D, 6x + 8y >= 100 … (i)
For vitamin E, 7x + 12y >= 120 …(ii)
Cost minimize is, C = 12x + 20y
From (i) and (ii), we get x = 15, y = 5/4
So, to minimize cost C = 12(15) + 20(5/4) = 205
So, the answer is option 1.
Q13 – Which of the following are quantities (in grams) of food X and Y respectively when the cost of food is minimum:
0 and 12 ½
15 and 5/4
120/7 and 0
0 and 10
Ans – (2)
Explanation – We get in question number 91, x = 15 and y = 5/4
So, the option 2 is the answer.
Q14 – Which of the following constrains when formulating the LPP ?
6x + 7y <= 100, 8x + 12y <= 120, x, y >= 0
6x + 8y <= 100, 7x + 12y <= 120, x, y >= 0
6x + 7y >= 100, 8x + 12y >= 120, x, y >= 0
6x + 8y >= 100, 7x + 12y >= 120, x, y >= 0
Ans – (4)
Explanation – We get in question number 91,
For vitamin D, 6x + 8y >= 100 … (i)
For vitamin E, 7x + 12y >= 120 …(ii)
So, the option 4 is the answer.
Q15 – The dual of the formulated LPP is:
1. | Max Z = 100u + 120vs.t.6u + 7v ≤ 128u + 12v ≤ 20u, v ≥ 0 |
2. | Max Z = 12u + 20vs.t.6u + 7v ≤ 1008u + 12v ≤ 120u, v ≥ 0 |
3. | Max Z = 100u + 120vs.t.6u + 7v ≤ 128u + 7v ≤ 20u, v are unrestricted |
4. | Max Z = 100u + 120us.t.6u + 7v ≥ 128u + 12v ≥ 20u, v ≥ 0 |
Ans – (1)
Explanation – We get in question number 91,
For vitamin D, 6x + 8y >= 100 … (i)
For vitamin E, 7x + 12y >= 120 …(ii)
Cost minimize is, C = 12x + 20y
The dual of the formulated LPP is
Max Z = 100u + 120v
s.t.
6u + 7v ≤ 12
8u + 12v ≤ 20
u, v ≥ 0
Q16 – Which of the following constrains when formulating the LPP?
6x + 7y <= 100, 8x + 12y <= 120, x, y >= 0
6x + 8y <= 100, 7x + 12y <= 120, x, y >= 0
6x + 7y >= 100, 8x + 12y >= 120, x, y >= 0
6x + 8y >= 100, 7x + 12y >= 120, x, y >= 0
Ans – (4)
Explanation – We get in question number 91,
For vitamin D, 6x + 8y >= 100 … (i)
For vitamin E, 7x + 12y >= 120 …(ii)
Also, x, y ≥ 0
Cost minimize is, C = 12x + 20y
Q17 – Which of the following graphs are trees?
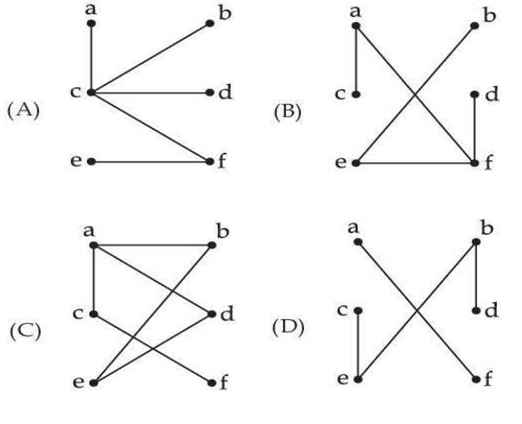
1. (a) and (b) only
2. (a), (b) and (d) only
3. (a) and (d) only
4. (a), (b), (c) and (d) only
Ans – (1)
Explanation –
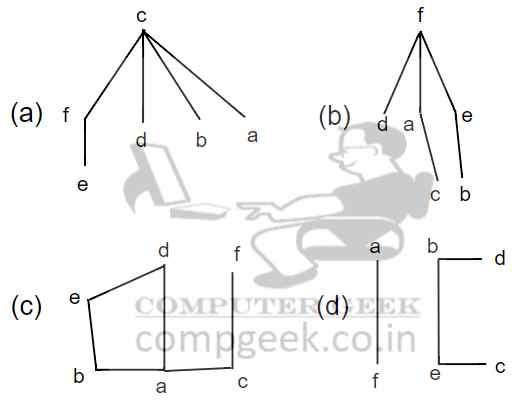
(a) and (b) are trees.
(c) is not a tree because adeb form a graph
(d) It is not hierarchical so that’s why not a tree.



