Sorting –
Arrangement of elements in a non-decreasing or non-increasing order.
Then a question comes to your mind that why is the arrangement of elements in a non-decreasing or non-increasing order only, why it is not in the increasing or decreasing order?
Ans – if you have an input of duplicate elements, then you can never say sort in increasing or decreasing order.
I will explain to you why…
Suppose input is 12 6 4 7 8 12 3
and you have to sort the number in an increasing (<) way,
so the output will be 3 4 6 7 8 12.
The input has 6 numbers but the output has only 5 numbers. because the input number 12 is not greater than the input number 12.
If you are searching elements in increasing order then you have to take only one 6. But a non-decreasing word can help to get the second 6.
.
Types of Sorting
1. Comparison Sort –
When sorting is based on comparing two elements.
It is a type of sorting algorithm that arranges a list of elements by comparing pairs of elements and swapping them if they are in the wrong order. The goal of a comparison sort is to reorder the elements in such a way that they are sorted in ascending or descending order based on a defined comparison function.
The best time complexity achievable for a comparison sort in worst-case is O(nlog n), where “n” represents the number of elements in the input list.
Example – Merge Sort, Quick Sort, Heap Sort, Insertion Sort, Bubble Sort, and Selection Sort.
.
2. In-place Sort –
An in-place sort is a type of sorting algorithm that rearranges the elements of a list or array within the same memory space, without requiring additional memory or auxiliary data structures proportional to the input size. In other words, the sorting process occurs directly within the original array or list without using any extra memory. It uses space complexity is theta (1).
Example – Quick Sort, bubble sort.
.
3. Stable Sort –
Suppose before sorting, there are two numbers (ai and aj) same in the input and suppose i and j are their indexes, and i comes before j, then after sorting in the output, if ai comes before aj then you can say, it is a stable sort.
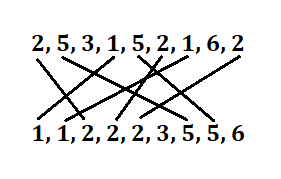
This means the first come first serve policy is applied in the stable sort.
.
4. Internal Sort –
Internal sort refers to the sorting of data that fits entirely within the main memory (RAM) of a computer system. The entire dataset can be accessed and manipulated directly in the computer’s RAM, which typically offers faster access times compared to external storage devices.
Example – Quick Sort, Merge Sort, Heap Sort, Insertion Sort, and Selection Sort.
.
5. External Sort –
External sort refers to the sorting of data that exceeds the available memory (RAM) of a computer system and needs to be stored and manipulated using external storage devices, such as hard disks, solid-state drives (SSDs), or magnetic tapes. This type of sorting is essential when the dataset is too large to fit entirely into the RAM, and the data must be read and written to and from external storage during the sorting process.
Example – B and B+ trees
.
6. Efficient Sort –
It refers to the process of arranging elements in a specific order within a dataset in a manner that minimizes the computational resources, such as time and memory, required to perform the sorting operation. Means Time & Space complexity is minimum.
Example – Merge Sort, Quick Sort, and Heap Sort, all of which have average-case time complexity of O(n log n).
.
7. Data Sensitive Sort –
The primary goal of data-sensitive sorting is to minimize the number of comparisons and swaps required to sort the data efficiently. By exploiting the inherent structure or order in the data, these algorithms can reduce the overall time complexity, especially in cases where the data is already partially ordered or nearly in sorted order. Best case ≠ Worst case.
.
How to measure Time and Space Complexity in a sorting algorithm
Time Complexity is number of operations and these number of operations in a sorting algorithm are in the category
- Key Comparisons
- Movement of keys
- Key interchange
Space Complexity is the number of bits used by the sorting algorithm. There can be any primary data structure which a sorting algorithm uses to generate the sorted output
- Stack
- Queue
- Linked list
- Array and many more
Test Yourself
Q1- Explain the difference between sorting in non-decreasing order and increasing order.
Sorting in non-decreasing order allows duplicate elements to be arranged in the sorted output, maintaining their original order. In contrast, sorting in increasing order does not consider duplicate elements separately, resulting in a shorter sorted list. For example, if the input is 12 6 4 7 8 6 3, sorting in non-decreasing order gives 3 4 6 6 7 8 12, while sorting in increasing order gives 3 4 6 7 8 12.
Q2- What is the main characteristic of a comparison sort, and why is it important?
The main characteristic of a comparison sort is that it arranges a list of elements by comparing pairs of elements and swapping them based on a defined comparison function. It is important because it allows us to define the order in which elements should appear in the sorted output.
Q3- Explain the concept of stability in a sorting algorithm.
Stability in a sorting algorithm refers to the property where elements with equal keys remain in their original order after sorting. In other words, if two elements have the same value and one appears before the other in the input, a stable sort ensures that the same order is maintained in the output.
Q4- What is the difference between an internal sort and an external sort?
An internal sort refers to sorting data that fits entirely within the computer’s main memory (RAM), while an external sort is used when the dataset exceeds the available RAM and needs to be stored and manipulated using external storage devices, such as hard disks or SSDs.
Q5- How does an in-place sort differ from other sorting algorithms?
An in-place sort rearranges the elements of a list or array directly within the same memory space without requiring additional memory proportional to the input size. Other sorting algorithms may need extra memory for auxiliary data structures during the sorting process.
Q6- What are the criteria to measure the efficiency of a sorting algorithm?
The efficiency of a sorting algorithm is typically measured using time complexity and space complexity. Time complexity represents the number of operations performed during the sorting process, while space complexity measures the additional memory used by the algorithm.






