Understanding Topological Sorting in Algorithm Design
.
Topological sorting is a technique used in the field of graph theory to arrange the vertices of a directed acyclic graph (DAG) in a linear ordering such that for every directed edge u -> v, the vertex u comes before the vertex v in the ordering.
Directed Acyclic Graph (DAG) – is a type of graph that consists of vertices (nodes) connected by directed edges, where each edge has a direction indicating a one-way relationship between vertices.
The term “acyclic” means that there are no cycles or loops in the graph, i.e., there is no sequence of edges that starts and ends at the same vertex.
The term “Topological Sorting” was first described by Kahn in 1962 by Kahn Algorithm.
.
Why “topological Sorting” name has “Sorting” in it
Topological sorting is named as such because it sorts the elements of a directed acyclic graph (DAG) in a particular order, known as a topological order.
In this context, “sorting” does not refer to the typical sorting of elements based on their numerical or alphabetical values, as in sorting algorithms like bubblesort or mergesort.
Instead, topological sorting aims to organize elements (often represented as vertices in a directed graph) in a linear order based on their dependencies, guaranteeing that no element appears before its requirements.
This sorting is necessary for operations like scheduling, where the order of execution must follow specific requirements or limitations. The resulting linear ordering is known as a topological order.
Topological sorting is possible even when the DAG has disconnected components.
.
Algorithm for Topological Sorting
- Start with any vertex in the graph.
- Perform a depth-first search traversal.
- During the traversal:
- Mark the current vertex as visited.
- Recursively visit all adjacent vertices (neighbours) that have not been visited yet.
- After visiting all neighbours, add the current vertex to a stack or list.
- After the DFS traversal is complete, the vertices will be stored in reverse order of their finishing times.
- Reverse the order of vertices obtained from the DFS traversal to get the topological sorting.
.
Example
We create a graph and, in that graph, depth first search will be applied according to the algorithm.

After the DFS traversal is complete, the vertices will be stored in the reverse order of their finishing time.
Reverse the order of vertices obtained from the DFS traversal to get the topological sorting.
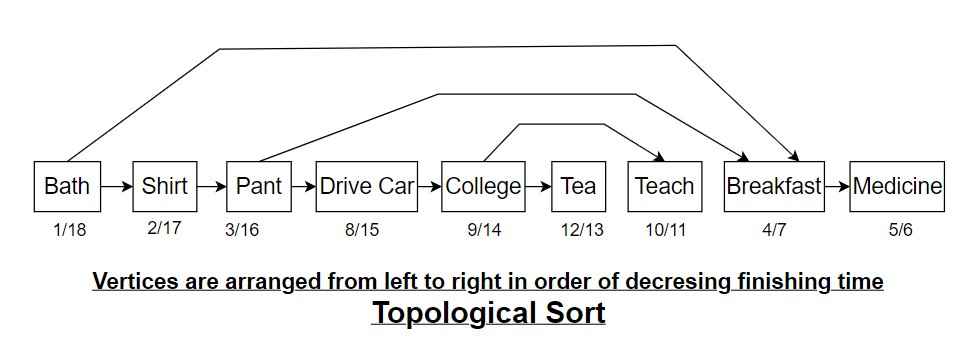
.
Source Code of Topological Sort
// COMPUTER GEEK – compgeek.co.in
// Write a program for Topological Sorting
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTICES 100
// Structure to represent a node in the adjacency list
typedef struct Node {
int vertex;
struct Node* next;
} Node;
// Structure to represent the adjacency list for each vertex
typedef struct {
Node* head;
} AdjList;
// Structure to represent the directed graph
typedef struct {
int numVertices;
AdjList* array;
} Graph;
// Function to create a new node
Node* createNode(int vertex) {
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->vertex = vertex;
newNode->next = NULL;
return newNode;
}
// Function to create a graph with ‘numVertices’ vertices
Graph* createGraph(int numVertices) {
Graph* graph = (Graph*)malloc(sizeof(Graph));
graph->numVertices = numVertices;
graph->array = (AdjList*)malloc(numVertices * sizeof(AdjList));
for (int i = 0; i < numVertices; ++i) {
graph->array[i].head = NULL;
}
return graph;
}
// Function to add an edge to the graph
void addEdge(Graph* graph, int src, int dest) {
Node* newNode = createNode(dest);
newNode->next = graph->array[src].head;
graph->array[src].head = newNode;
}
// Function to perform DFS traversal
void DFS(Graph* graph, int vertex, int visited[], int* index, int stack[]) {
visited[vertex] = 1;
Node* temp = graph->array[vertex].head;
while (temp != NULL) {
int adjVertex = temp->vertex;
if (!visited[adjVertex]) {
DFS(graph, adjVertex, visited, index, stack);
}
temp = temp->next;
}
stack[(*index)++] = vertex;
}
// Function to perform topological sorting
void topologicalSort(Graph* graph) {
int visited[MAX_VERTICES] = {0};
int stack[MAX_VERTICES];
int index = 0;
for (int i = 0; i < graph->numVertices; ++i) {
if (!visited[i]) {
DFS(graph, i, visited, &index, stack);
}
}
printf(“Topological Sorting: “);
for (int i = index – 1; i >= 0; –i) {
printf(“%d “, stack[i]);
}
printf(“\n”);
}
int main() {
int numVertices, numEdges, src, dest;
printf(“Enter the number of vertices: “);
scanf(“%d”, &numVertices);
Graph* graph = createGraph(numVertices);
printf(“Enter the number of edges: “);
scanf(“%d”, &numEdges);
printf(“Enter the edges (source destination):\n”);
for (int i = 0; i < numEdges; ++i) {
scanf(“%d %d”, &src, &dest);
addEdge(graph, src, dest);
}
topologicalSort(graph);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Topological Sorting
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
class Graph {
int numVertices;
vector<vector<int>> adjList;
public:
Graph(int V) {
numVertices = V;
adjList.resize(V);
}
void addEdge(int src, int dest) {
adjList[src].push_back(dest);
}
void DFS(int v, vector<bool>& visited, stack<int>& Stack) {
visited[v] = true;
for (int neighbor : adjList[v]) {
if (!visited[neighbor]) {
DFS(neighbor, visited, Stack);
}
}
Stack.push(v);
}
void topologicalSort() {
stack<int> Stack;
vector<bool> visited(numVertices, false);
for (int i = 0; i < numVertices; ++i) {
if (!visited[i]) {
DFS(i, visited, Stack);
}
}
cout << “Topological Sorting: “;
while (!Stack.empty()) {
cout << Stack.top() << ” “;
Stack.pop();
}
cout << endl;
}
};
int main() {
int numVertices, numEdges, src, dest;
cout << “Enter the number of vertices: “;
cin >> numVertices;
Graph graph(numVertices);
cout << “Enter the number of edges: “;
cin >> numEdges;
cout << “Enter the edges (source destination):\n”;
for (int i = 0; i < numEdges; ++i) {
cin >> src >> dest;
graph.addEdge(src, dest);
}
graph.topologicalSort();
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Topological Sorting
import java.util.*;
class Graph {
private int numVertices;
private List<List<Integer>> adjList;
public Graph(int V) {
numVertices = V;
adjList = new ArrayList<>(V);
for (int i = 0; i < V; ++i) {
adjList.add(new ArrayList<>());
}
}
public void addEdge(int src, int dest) {
adjList.get(src).add(dest);
}
public void DFS(int v, boolean[] visited, Stack<Integer> stack) {
visited[v] = true;
for (int neighbor : adjList.get(v)) {
if (!visited[neighbor]) {
DFS(neighbor, visited, stack);
}
}
stack.push(v);
}
public void topologicalSort() {
Stack<Integer> stack = new Stack<>();
boolean[] visited = new boolean[numVertices];
Arrays.fill(visited, false);
for (int i = 0; i < numVertices; ++i) {
if (!visited[i]) {
DFS(i, visited, stack);
}
}
System.out.print(“Topological Sorting: “);
while (!stack.isEmpty()) {
System.out.print(stack.pop() + ” “);
}
System.out.println();
}
}
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print(“Enter the number of vertices: “);
int numVertices = scanner.nextInt();
Graph graph = new Graph(numVertices);
System.out.print(“Enter the number of edges: “);
int numEdges = scanner.nextInt();
System.out.println(“Enter the edges (source destination):”);
for (int i = 0; i < numEdges; ++i) {
int src = scanner.nextInt();
int dest = scanner.nextInt();
graph.addEdge(src, dest);
}
graph.topologicalSort();
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for Topological Sorting
from collections import defaultdict
class Graph:
def __init__(self, V):
self.numVertices = V
self.adjList = defaultdict(list)
def addEdge(self, src, dest):
self.adjList[src].append(dest)
def DFS(self, v, visited, stack):
visited[v] = True
for neighbor in self.adjList[v]:
if not visited[neighbor]:
self.DFS(neighbor, visited, stack)
stack.append(v)
def topologicalSort(self):
visited = [False] * self.numVertices
stack = []
for i in range(self.numVertices):
if not visited[i]:
self.DFS(i, visited, stack)
print(“Topological Sorting:”, *stack[::-1])
if __name__ == “__main__”:
numVertices = int(input(“Enter the number of vertices: “))
graph = Graph(numVertices)
numEdges = int(input(“Enter the number of edges: “))
print(“Enter the edges (source destination):”)
for _ in range(numEdges):
src, dest = map(int, input().split())
graph.addEdge(src, dest)
graph.topologicalSort()
Enter the number of vertices: 9
Enter the number of edges: 9
Enter the edges (source destination):
0 1
0 3
1 2
2 3
2 5
3 4
5 6
6 7
6 8
Topological Sorting: 0 1 2 5 6 7 8 3 4
=== Code Execution Successful ===
Time Complexity
The time complexity of topological sort depends on the algorithm used. When using depth-first search (DFS) to perform topological sorting, the time complexity is O(V+E), where V is the number of vertices and E is the number of edges in the graph.
It takes O(1) time to move each visited vertex into the front of a linked list.
.
Space Complexity
The space complexity for representing the graph itself is typically O(V+E), where V is the number of vertices and E is the number of edges. This space is required to store the connections between vertices in the graph.
In some implementations, a stack or list may be used to store the sorted order of vertices obtained during the DFS traversal. The space complexity for this stack or list is also O(V).
Overall, the space complexity of topological sorting using depth-first search (DFS) is typically O(V+E).
.
Advantages
Dependency Resolution – Topological sorting is essential for resolving dependencies between tasks or events, ensuring that all prerequisites are met before a task is executed.
Task Scheduling – It facilitates efficient scheduling of tasks in various domains such as project management, job scheduling, and workflow optimization.
Optimized Execution Order – By organizing tasks based on their dependencies, it helps in determining the optimal order of execution, minimizing delays and maximizing efficiency.
Cycle Detection – It can be used to detect cycles in directed graphs, helping prevent infinite loops or circular dependencies.
Algorithmic Applications – Topological sorting serves as a fundamental building block for various algorithms, including shortest path algorithms, critical path analysis, and network flow algorithms.
.
Disadvantages
Limited to Directed Acyclic Graphs (DAGs) – Topological sorting can only be performed on directed acyclic graphs (DAGs). It cannot handle graphs with cycles, as cyclic dependencies make it impossible to determine a valid topological order.
Multiple Valid Orderings – In some cases, there may be multiple valid topological orderings for a given DAG. The algorithm may produce different orderings based on the order of traversal, leading to ambiguity in selecting a specific order.
Complexity – The time complexity of topological sorting is O(V+E), which can be relatively high for large graphs with many vertices and edges. Additionally, the space complexity also increases with the size of the graph.
.
Applications
Task Scheduling – Topological sorting is widely used in project management and job scheduling to determine the order of tasks that need to be executed based on their dependencies. It ensures that tasks are performed in the correct sequence, considering prerequisites and dependencies.
Course Prerequisites – In academic institutions, topological sorting is used to determine the sequence of courses that students must take based on their prerequisites. It ensures that students have the necessary background knowledge before enrolling in advanced courses.
Dependency Resolution – In software development, topological sorting is used to resolve dependencies between modules, libraries, and packages. It helps in managing software dependencies and ensuring that all required components are available before building or deploying the software.
Pipeline Execution – In data processing pipelines and workflows, topological sorting is used to define the order in which tasks should be executed. This ensures that data processing tasks are performed in a logical sequence, optimizing resource utilization and throughput.
Critical Path Analysis – In project management, topological sorting is used for critical path analysis to identify the longest path through a project’s tasks. This helps in identifying tasks that are critical to the project’s timeline and scheduling resources effectively.
Course Scheduling – Academic institutions use topological sorting to schedule courses and class timings, taking into account constraints such as classroom availability, teacher availability, and course prerequisites.
Network Routing – In computer networks, topological sorting is used to determine the optimal routing paths between nodes. It helps in efficient packet routing and network optimization by considering the network topology and link dependencies.
Test Yourself
Q1- How does topological sorting differ from traditional sorting algorithms like quicksort or mergesort?
Topological sorting organizes elements (vertices) based on their dependencies in a directed acyclic graph (DAG), whereas traditional sorting algorithms arrange elements based on their numerical or alphabetical values. Topological sorting does not compare elements directly but rather considers their relationships.
Q2- Describe the algorithm for performing topological sorting using depth-first search (DFS).
- The algorithm involves performing a DFS traversal on the graph, marking vertices as visited, and recursively visiting adjacent vertices.
- After the traversal, vertices are stored in reverse order of their finishing times, which represents the topological order.
- Finally, the order is reversed to obtain the topological sorting.
Q3- Discuss the time complexity of the topological sorting algorithm.
The time complexity of topological sorting using DFS is O(V + E), where V is the number of vertices and E is the number of edges in the graph. This complexity arises from visiting each vertex and its adjacent vertices once during the DFS traversal.
Q4- Explain the concept of a directed acyclic graph (DAG) and why topological sorting is applicable only to DAGs.
A directed acyclic graph (DAG) is a graph with directed edges and no cycles. Topological sorting is applicable only to DAGs because cycles introduce ambiguity in the ordering, making it impossible to establish a linear order based on dependencies.
Q5- Provide real-world examples where topological sorting is commonly used.
Topological sorting is used in various domains such as
- project management (for task scheduling),
- Academic institutions (for course prerequisites),
- Software development (for dependency resolution), and
- Network routing (for optimal packet routing).
Q6- What are the advantages of topological sorting in algorithm design?
Advantages include efficient
- task scheduling,
- optimized execution order,
- cycle detection,
- algorithmic applications, and
- the ability to resolve dependencies in tasks or events.
Q7- Discuss the limitations or disadvantages of topological sorting.
Limitations include its applicability only to DAGs, the possibility of multiple valid orderings, complexity in implementation and understanding, and potential performance issues for large graphs.
Q8- What type of graph is required for topological sorting?
1. Undirected graph
2. Directed cyclic graph
3. Directed acyclic graph (DAG)
4. Bipartite graph
Ans – (3)
Explanation – Topological sorting is applicable only to directed acyclic graphs (DAGs).
Q9- What is the primary purpose of topological sorting?
1. Sorting elements alphabetically
2. Sorting elements numerically
3. Resolving dependencies
4. Detecting cycles in graphs
Ans – (3)
Explanation – The primary purpose of topological sorting is to resolve dependencies between elements or tasks.
Q10- What does a directed acyclic graph (DAG) signify in the context of topological sorting?
1. Graph with cycles
2. Graph with no vertices
3. Graph with no edges
4. Graph with directed edges and no cycles
Ans – (4)
Explanation – A directed acyclic graph (DAG) is a prerequisite for performing topological sorting.






