Unit 1
Deterministic Finite Automaton (DFA)- Definition, Representation, Acceptability of a String and Language, Non Deterministic Finite Automaton (NFA), Equivalence of DFA and NFA, NFA with ε-Transition, Equivalence of NFA’s with and without ε-Transition
Q21 – Which is true for Dead State?
It cannot be reached anytime
There is no necessity of the state
If control enters no way to come out from the state
If control enters FA deads
Ans – (3)
Explanation – A dead state (also called a trap state) in a finite automaton is a state from which no accepting state can be reached. Once the automaton enters this state, it keeps looping inside the same state for all input symbols and can never reach a final state.
Q22 – Two states p and q of a finite automaton are said to be equivalent if
they have the same number of incoming and outgoing transitions
they always lead to acceptance or rejection for the same set of input strings
both states are final states
both states have the same number of transitions and symbols
Ans – (2)
Explanation – Two states of a finite automaton are called equivalent states if, starting from either state, the automaton accepts or rejects exactly the same strings. In other words, no input string can distinguish between the two states. The number of transitions, number of states, or whether both states are final is not sufficient to decide equivalence. What matters is the future behavior of the automaton for all possible inputs.
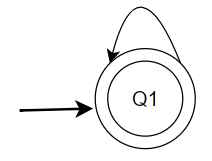
Q23 – What does the following figure most correctly represents?

The figure represents the initial as well as the final state with an iteration of x
Final state with loop x
Transitional state with loop x
Initial state as well as final state with loop x
Insufficient Data
Ans – (3)
Explanation –
an incoming arrow from nowhere, which indicates the initial (start) state,
a double circle, which indicates a final (accepting) state, and
a self-loop labeled x, which means the automaton can stay in the same state while reading symbol x any number of times.
Q24 – The Tuples for NDFA
∑, Q, q0, F, δ
Q, q0, F, δ
Θ, Q, q0, F, δ
F, Q, Δ, q0, δ
Ans – (1)
Explanation – A Non-Deterministic Finite Automaton (NDFA / NFA) is formally defined by a 5-tuple:
M = (Q, Σ, δ, q₀, F)
Where
Q – finite set of states
Σ – input alphabet
δ – transition function
q₀ – initial (start) state
F – set of final (accepting) states
Q5 – NFAs are ___ DFAs.
Larger than
More expressive than
Less expressive than
Equally expressive as
Ans – (4)
Explanation – NFAs and DFAs recognize exactly the same class of languages, which are called regular languages.
So, in terms of expressive power (what languages they can describe), NFAs are not more powerful than DFAs.
Even though NFAs may look more flexible because they allow
multiple possible next states, and
ε-transitions,
every NFA can be converted into an equivalent DFA that accepts the same language.
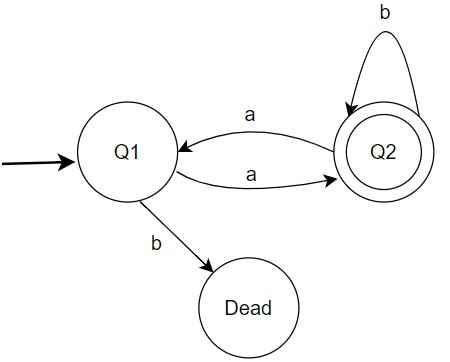
Q26 – Which of the following will not be accepted by the following DFA?
ababaabaa
abbbaa
abbbaabb
abbaabbaa
Ans – (1)
Explanation – From the DFA diagram, Q1 is the start state, Q2 is the only final state, and Dead is the trap state. The transitions are simple – from Q1, input a moves the DFA to Q2, but input b sends it directly to the Dead state. From Q2, input b keeps the DFA in Q2, while input a sends it back to Q1.
For option 1 – ababaabaa, the DFA goes from Q1 to Q2 on a, stays in Q2 on b, moves back to Q1 on a, and then reads b at Q1, which immediately sends it to the Dead state. Once the DFA enters the Dead state, the string is rejected.
All other strings (abbbaa, abbbaabb, abbaabbaa) never read b while in Q1 and finally end in Q2, so they are accepted.
Q27 – An NFA’s transition function returns
A Boolean value
A state
A set of states
An edge
Ans – (3)
Explanation – In a Non-Deterministic Finite Automaton (NFA), for a given current state and input symbol, the automaton can move to zero, one, or many next states.
Because multiple next states are possible, the transition function of an NFA must return a set of states, not a single state.
Formally, the transition function of an NFA is defined as
δ : Q × Σ → 2^Q
Q28 – Conversion of a DFA to an NFA
Is impossible
Requires the subset construction
Is Chancy
Is nondeterministic
Ans – (2)
Explanation – In many textbooks and MCQ contexts, conversion between DFA and NFA is discussed in terms of formal construction techniques. When a DFA is treated as a special case and we want to represent it in the general NFA framework, the subset construction idea is referenced as the standard method used in automata conversions.
Q29 – An NFA may be converted to a DFA using
Induction
A construction
Contradiction
Compilation
Ans – (2)
Explanation – An NFA can be converted into an equivalent DFA by using a systematic construction method, which is commonly known as the subset construction (or powerset construction).
Q30 – The subset construction shows that every NFA accepts a
String
Function
Regular language
Context-free language
Ans – (3)
Explanation – The subset construction is a method used to convert an NFA into an equivalent DFA.
This conversion proves that whatever language is accepted by an NFA can also be accepted by a DFA.
And since DFAs recognize only regular languages, it follows that every language accepted by an NFA is a regular language.
Q31 – Which statement is correct?
All NFAs are DFAs.
All NFAs are not DFAs.
Both (A) and (B)
None of these
Ans – (2)
Explanation –
A DFA is a special type of NFA where
for every state and input symbol, there is exactly one next state, and
ε-transitions are not allowed.
An NFA, on the other hand, may have
multiple possible next states for the same input symbol, or
ε-transitions.
Because of these extra features, not every NFA satisfies the strict rules of a DFA.
So, all NFAs cannot be called DFAs.
Q32 – For each symbolic representation of the alphabet, there is only one state transition in?
DFA
NFA
FA
All of these
Ans – (1)
Explanation – Σ₁* = {ε, 0, 00, …} ⊆ Σ₂* (since both contain ε, 0, 00…).In a Deterministic Finite Automaton (DFA), for each state and for each input symbol from the alphabet, there is exactly one defined transition. This is the main property that makes the automaton deterministic.
Q33 – Construct a NDFA for the following regular expression
(a∪b)*aba(a∪b)*
a
b
c
d
Ans – (1)
Q34 – In which of the following, it’s not mandatory to generate transition for each alphabet in the language from a given state to its final state?
Ans – (3)
Explanation –
In a Non-Deterministic Finite Automaton (NFA), it is not mandatory to define a transition for every input symbol from a given state. An NFA may have
no transition,
one transition, or
multiple transitions
for the same input symbol.
Q35 – Which is the application of NFA
A regular language is produced by union of two regular languages
The concatenation of two regular languages is regular
The Kleene closure of a regular language is regular
All of the mentioned
Ans – (4)
Explanation – NFAs are very useful in proving closure properties of regular languages. Using NFA constructions, we can easily show that regular languages remain regular under different operations.
Q36 – When it is not fixed that with a specific input where to go next on which state, then it is called?
DFA
NFA
DFSA
None of these
Ans – (2)
Explanation –
When it is not fixed that for a given state and a specific input symbol, the automaton will go to which next state, the automaton is called a Non-Deterministic Finite Automaton (NFA).
In an NFA, for the same input symbol,
there may be multiple possible next states, or
there may be no transition at all.
Q37 – The password to the email account=”$Password$”. The total number of states required to make a password-pass system using DFA would be __________
14 states
13 states
12 states
A password pass system cannot be created using DFA
Ans – (3)
Explanation –
Let us first count the number of symbols in the password.
$ P a s s w o r d $
Total symbols = 10
To design a password-checking DFA, the rule is very simple:
For a password of length n,
n + 1 states are needed to match the password step by step
+ 1 dead (trap) state is required for wrong input
So, total states required
= 10 (symbols) + 1 (start state) + 1 (dead state)
= 12 states
Q38 – Let ∑= {a, b, …. z} and A = {Hello, World}, B= {Input, Output}, then (A*∩B) U (B*∩A) can be represented as
{Hello, World, Input, Output, ε}
{Hello, World, ε}
{Input, Output, ε}
{}
Ans – (1)
Explanation –
A* ∩ B
B = {Input, Output}
None of these appear in A*.
So, A* ∩ B = { }
B* ∩ A
A = {Hello, World}
None of these appear in B*.
So, B* ∩ A = { }
then { } U { } = { }
Q39 – The relation between NFA-accepted languages and DFA accepted languages is
>
<
=
<=
Ans – (3)
Explanation –
The class of languages accepted by NFAs is exactly the same as the class of languages accepted by DFAs. Both types of automata recognize regular languages.
Even though an NFA looks more flexible because it allows
multiple transitions for the same input symbol, and
ε-transitions,
every NFA can be converted into an equivalent DFA using subset construction.
Q40 – Which statement is correct about DFA?
All DFAs are derived from NFAs.
All NFAs are derived from DFAs.
Both can’t be derived from each other
Both (A) and (B)
Ans – (1)
Explanation –
A DFA is actually a special case of an NFA.
In an NFA, we are allowed to have
multiple next states for the same input, or
ε-transitions.
If we restrict an NFA so that
there is exactly one transition for each input symbol, and
no ε-transitions,
then it becomes a DFA.
So, every DFA can be seen as an NFA with extra restrictions.