Subset Sum Problem

Introduction

.

The Subset Sum Problem (SSP) is a classic problem in computer science and combinatorial optimization. It belongs to the category of decision problems, where the task is to determine whether there exists a subset of numbers in a given set that adds up to a particular value.

This problem is particularly famous because it is a special case of the more general Knapsack Problem and is known for being NP-complete, meaning it is at least as hard as the hardest problems in the class NP.

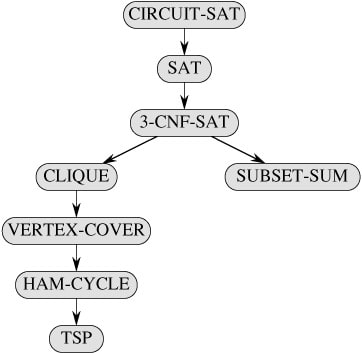
If you have read Thomas H. Cormen’s book, you will notice that the below diagram is printed in it.

.

Clique problem, Vertex-Cover problem, Hamiltonian Cycle problem, Travelling Salesman problem and Subset Sum problem are all can be reduced by 3-CNF-SAT problem, but why is Subset sum problem written on the different sub-section of the diagram?

Because the clique, vertex-cover, Hamiltonian cycle and tsp are all graph problems. But Subset Sum is not a graph problem so that is why it is written on the different sub-section.

.

Problem Definition

“Determine whether there exists any non-empty subset of 𝑆 such that the sum of its elements equals 𝑇.“

In other words, the goal is to find any subset 𝑆′⊂𝑆 where the sum of the elements in 𝑆’ is exactly 𝑇.

Input

• A finite set 𝑆 of 𝑛 integers
• An integer 𝑇, the target sum

Output

• True if there exists a subset of 𝑆 whose sum is equal to 𝑇.
• False otherwise

.

Time Complexity

There are many ways to solve a subset sum problem. It can be solved by the Naïve method, Recursive method, Dynamic Programming and Backtracking.

In Naïve method, the time complexity is O(n.2ⁿ) that is, exponential time.

In Recursive Method, the time complexity is O(2ⁿ) that is, exponential time.

In Dynamic Programming, the time complexity is O(n.t) where t is ‘target sum’. If the target sum (t) is large, then the time complexity is pseudo-polynomial (Not Truly Polynomial).

Pseudo-polynomial time – The complexity is polynomial in the numeric value of inputs. But if that number is very large, then it develops an exponential growth regarding input size.

In Backtracking, the time complexity is O(2ⁿ) that is, exponential time.

.

.

The problem Subset Sum belongs to the class NP-Complete in computational complexity theory. That is to say two things,

NP – The correctness of the solution to the problem can be verified in polynomial time.

NP-Hard – At least as hard as the hardest problems in NP, and until now, no polynomial-time algorithm is known to solve all the problems in NP-complete.

.

Historical Context

The phrase “Subset Sum Problem” may have originated with the advent of complexity theory and computational complexity classes in the 1970s.

Richard Karp’s influential 1972 paper, “Reducibility Among Combinatorial Problems,” included the Subset Sum Problem as one of 21 NP-complete problems, which was a crucial milestone in bringing it into the spotlight of computational theory.

In the early 1970s, academics like as Stephen Cook and Leonid Levin developed and formalized complexity theory and NP-completeness, which helped to create and name norms for many computer issues, including the Subset Sum Problem.

.

Reduction of 3-SAT Problem to Subset Sum Problem

The 3-SAT problem is the first problem that can be proved by scientists, an NP-Complete problem. Reduction of the 3-SAT problem to the Subset Sum problem will prove that this problem is also an NP-Complete problem.

The Subset Sum Problem asks whether some numbers from a set can sum up to some target value. This reduction therefore shows that these two problems are equally difficult to solve.

.

Steps for Reduction

1. Write a 3SAT formula F with variables X1, X2, …, Xn and clauses C1, C2, …, Cm where each clause has exactly three literals.
2. For each variable Xi, create two values True(i) and False(i) of n + m digits.

• • Set the ith bit of True(i) and False(i) to 1.
  • If variable Xi is in the clause Cj, then cell(Xi, Cj) = 1
  • If variable ¬Xi is in the clause Cj, then cell(¬xi, Cj) = 1

3. For each clause Cj, create Sj and ¬Sj.
4. Assign Sj and ¬Sj in the column Cj to 1.
5. Create sum t of length n+m

• • The first n bits of variables are all 1 (to ensure every variable is assigned a value).
  • The last m bits of t are all 3 (to satisfy every clause).

6. If a subset occurs equal to the t, then 3SAT to Subset Sum is successful.
7. Otherwise, unsuccessful.

.

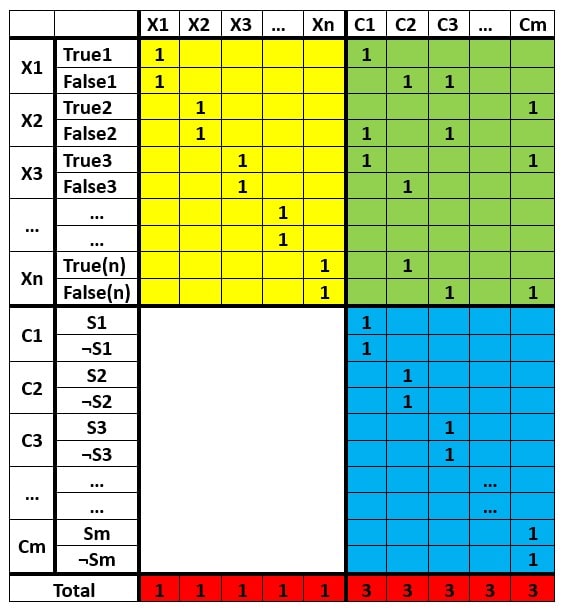
Understand how this table is formed?

1. Yellow Part –

• • The columns are the variables X1, X2, X3, … Xn
  • The rows are the variables but in the form of True1 and False1 for X1, True2 and False2 for X2, and same for Xn.
  • Each variable Xi can either be Xi (true) or ¬Xi (false). For each variable X1​, two rows are created – one for True1 (when X1 is true) and another for False1 (when X1 is false).
  • In these rows, the column for X1​ will have a value of 1, while all other columns in the comes after the 1’s will have 0s. Same for X2. True2 and False2 is 1 in the column X2.

.

2. Green Part –

• • If Xj comes in the Cj, then the cell contains 1 otherwise 0.
  • If ¬Xj comes in the Cj, then the cell contains 1 otherwise 0.
  • Every clause contains 3 variables. So, every column of Cj contains only three 1’s.

.

3. Blue Part –

• • In the table, the rows and columns include C1, C2, C3, …, Cm which represent the slack variables. These slack variables are denoted as Sj and ¬Sj​, where Sj​ corresponds to satisfying clause Cj​ and ¬Sj​ corresponds to not satisfying clause Cj​.
  • For example, S1​ and ¬S1​, which are part of clause C1​, will have a value of 1 in the C1 column, while all other columns will have 0s.
  • Similarly, all other slack variables will also have a value of 1 only in their respective clause’s column and 0s in all other columns.
  • This ensures that each slack variable only affects the satisfaction of its own clause and does not interfere with the others.

.

4. Red Part –

• • In the red part, called the total row, it computes a sum of the values. There is n 1’s in this row, which correspond to the n variables.
  • Let’s look at column 1 as an example. This column is for X1, and in the rows, True1 and False1 each have a value of 1. Normally, their sum would be 2, but that’s not right here because, for any clause, either X1 is true (True1) or ¬X1 is true (False1) but not both at once. A variable can’t both be true and false within the same clause (like X1 V ¬X1).
  • Therefore, the only value chosen for the Xi must be one of True(i) or False(i). This makes the total value in column exactly 1, which indicates consistent truth assignment for all of the variables.

.

5. Orange part –

• There is always a sum of 3 in the orange part. It denotes the clauses so number of columns in orange part is equal to number of clauses.
• For a formula to be satisfiable, each clause must have at least one variable that is true. Example- If the statement for a clause is (X1 ∨ ¬X2 ∨ ¬X3), then it is True when X1 is true, otherwise, clause is also true when X2 is false or X3 is false. That is, at least one of the variables in the clause must satisfy the clause (be true).
• Now, from the green box you can clearly observe that in every column there is only three 1’s because this is the 3-SAT problem where in every clause exactly three variables are involved. Three 1’s represent the variables are involved inside the clause.
• If any of these three variables satisfy the clause-that is, either Xi = true or ¬Xi = false, only one “1” will be counted from the contribution of the variables to the total. The other two variables will contribute 0 because they do not satisfy the clause.
• In addition to this, the blue part introduces two slack variables for every clause that are set to 1. These slack variables make sure that the total for each clause will always equal 3. 1 from the variable that satisfies the clause and 2 from the slack variables. Therefore, the sum of each column is 3, ensuring that the clause is satisfied and the equation is true.
• If two variables are true in a clause, then, 2 will be the total that comes from the variable because two “1s” will come out from those true variables plus one slack variable which will belong to the blue part contributing 1. So, the total again will be 3.
• If each of the three literals in a clause is true, so each will contribute 1 to the total. We do not need to use any slack variables from the blue part, Because the total for the clause is 3 in this case.
• As a result, this logic guarantees that at least one of the three possible cases of one variable true (1 + 2 slack = 3), two variables true (2 + 1 slack = 3) or all three variables true ends with (3 + 0 slack = 3).

.

Example –

F = (X1 V ¬X2 V X3) Λ (¬X1 V X2 V ¬X3) V (X1 V ¬X2 V ¬X3)

So, the table is of the form

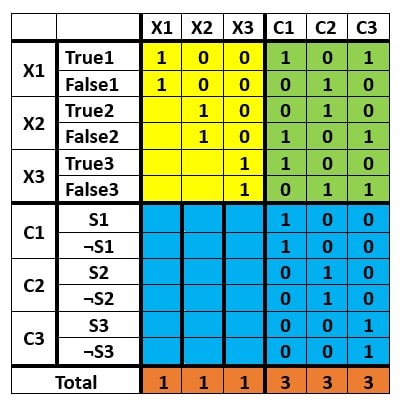
In this table, X1 (True1) number is 100101. Also, X1 (False1) number is 100010.

So, all the numbers in the table are – {100101, 100010, 10010, 10101, 1100, 1011, 100, 100, 10, 10, 1, 1} and we have to select a subset whose sum (total) is 111333.
Also, these numbers are in the decimal base.

The subset is {100101, 10010, 1011, 100, 100, 10, 1}, and it is shown with dark red color in the below table.

When we add all these numbers together, the total sum becomes 111333.

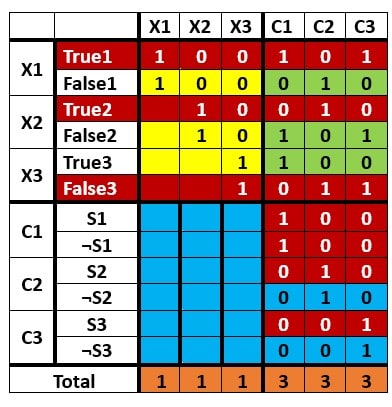
Let’s verify from the above example. The subset sum problem is solved and we need to solve 3-SAT problem by the solution of subset sum.

By seeing the x_i and ¬x_i in the dark red colour, the row decides true or false of the variable.

In the table, dark red colour signifies that

First variable x1 = True,

Second variable x2 = True,

Third variable x3 = False

F = (X1 V ¬X2 V X3) Λ (¬X1 V X2 V ¬X3) V (X1 V ¬X2 V ¬X3)

F = (True V False V False) ∧ (False V True V True) Λ (True V False V True)

F = True ∧ True ∧ True

F = True

Hence, 3-SAT Problem is true. it means that solving Subset Sum Problem would allow us to solve 3-SAT as well.