Strassen’s Algorithm: Fast Matrix Multiplication
Introduction
Strassen’s Algorithm is a revolutionary approach in the field of Algorithm Design & Analysis that improved the efficiency of matrix multiplication.
Traditional matrix multiplication algorithms, such as the naive approach, exhibit a time complexity of O(n3), which can become a bottleneck when dealing with large matrices.
Volker Strassen invented Strassen’s algorithm in 1969. The algorithm is a matrix multiplication algorithm for linear algebra. Strassen’s Algorithm offers a more efficient alternative, with a time complexity of approximately O(n^log2(7)) which is O(n2.81).
Let’s go into the inner workings of Strassen’s Algorithm and understand how it optimizes matrix multiplication.
.
Strassen’s Algorithm – Divide and Conquer
Strassen’s Algorithm employs a divide-and-conquer strategy to reduce the number of multiplications required to compute the matrix product. The algorithm breaks down the input matrices into smaller submatrices, each with dimensions halved. This recursive subdivision continues until the base case is reached, typically matrices of size 1×1.
.
Only Seven Multiplications needed
Strassen’s Algorithm uses just seven multiplications every recursive step, as compared to the traditional method, which takes eight different multiplications to compute each element of the resultant matrix. The approach considerably reduces the overall number of multiplications required by intelligently combining these seven multiplications.
.
Intermediate Matrix Products
Strassen’s Algorithm computes intermediate matrix products, which are combinations of the submatrices, during the recursive calls. These intermediate products are created by using specific equations to add or subtract correctly sized submatrices. The algorithm runs these equations iteratively until the beginning case is reached.
.
Combining Intermediate Products
After reaching the beginning situation and reducing the submatrices to 1×1 matrices, the algorithm continues merging the intermediate products to achieve the final output. Strassen’s Algorithm effectively combines these intermediate results by using addition and subtraction operations on correctly sized submatrices.
.
Working of Strassen’s Algorithm
This algorithm makes use of the same divide and conquer approach as in the matrix multiplication, but instead uses only 7 recursive multiplications rather than 8.
Here we can save one recursive call, but have several new additions of n/2*n/2 matrices.
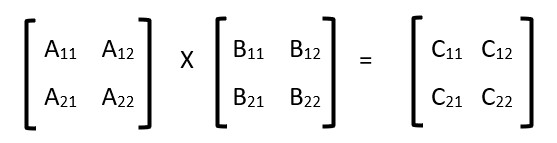
Product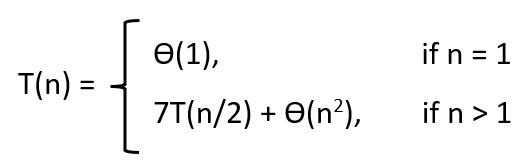
P1 = A11 * (B12 – B22)
P2 = (A11 + A12) * B22
P3 = (A21 + A22) * B11
P4 = A22 * (B21 – B11)
P5 = (A11 + A22) * (B11 + B22)
P6 = (A12 – A22) * (B21 + B22)
P7 = (A11 – A21) * (B11 + B12)
.
Matrix C
C11 = P5 + P4 – P2 + P6
C12 = P1 + P2
C21 = P3 + P4
C22 = P5 + P1 – P3 – P7
In this example,
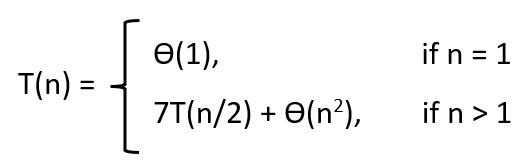
From master’s theorem
Time Complexity = O(n^log27) or O(n2.81)
Which beats the divide & conquer approach asymptotically.
.
Limitations and Considerations
While Strassen’s Algorithm offers improved time complexity, it does have some limitations and considerations to keep in mind.
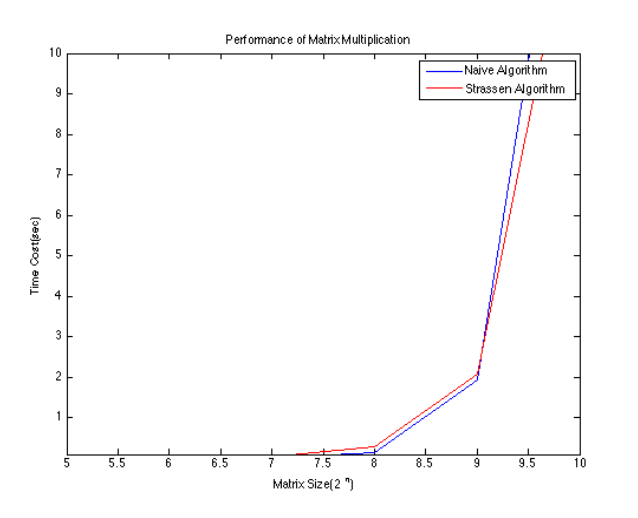
From the diagram, we can see that the naïve algorithm or traditional matrix multiplication has a lower time cost than the Strassen’s multiplication in the first halve.
But later on, in the second halve, the naïve multiplication has a higher time complexity than the Strassen’s multiplication.
.
Algorithm for Strassen’s Method
1. Divide the input matrices, A and B, into four equally sized submatrices
A11, A12, A21, and A22 for matrix A
B11, B12, B21, and B22 for matrix B
.
2. Create seven new matrices, P1 to P7, as follows
P1 = A11 * (B12 – B22)
P2 = (A11 + A12) * B22
P3 = (A21 + A22) * B11
P4 = A22 * (B21 – B11)
P5 = (A11 + A22) * (B11 + B22)
P6 = (A12 – A22) * (B21 + B22)
P7 = (A11 – A21) * (B11 + B12)
.
3. Recursively compute the following intermediate matrices
C11 = P5 + P4 – P2 + P6
C12 = P1 + P2
C21 = P3 + P4
C22 = P5 + P1 – P3 – P7
4. Combine the intermediate matrices to form the resulting matrix, C
// COMPUTER GEEK – compgeek.co.in
// Write a Program to multiply two matrices from Strassen’s Algorithm
#include <stdio.h>
#include <stdlib.h>
// Function to allocate memory for a matrix
int** allocateMatrix(int size) {
int** matrix = (int**)malloc(size * sizeof(int*));
for (int i = 0; i < size; i++)
matrix[i] = (int*)malloc(size * sizeof(int));
return matrix;
}
// Function to deallocate memory of a matrix
void deallocateMatrix(int** matrix, int size) {
for (int i = 0; i < size; i++)
free(matrix[i]);
free(matrix);
}
// Function to add two matrices
void addMatrix(int** A, int** B, int** C, int size) {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
C[i][j] = A[i][j] + B[i][j];
}
}
}
// Function to subtract two matrices
void subtractMatrix(int** A, int** B, int** C, int size) {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
C[i][j] = A[i][j] – B[i][j];
}
}
}
// Function to multiply two matrices using Strassen’s Algorithm
void strassenMultiplication(int** A, int** B, int** C, int size) {
if (size <= 4) {
// Base case: Use naive matrix multiplication for small matrices
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
C[i][j] = 0;
for (int k = 0; k < size; k++) {
C[i][j] += A[i][k] * B[k][j];
}
}
}
return;
}
int newSize = size / 2;
// Creating submatrices
int** A11 = allocateMatrix(newSize);
int** A12 = allocateMatrix(newSize);
int** A21 = allocateMatrix(newSize);
int** A22 = allocateMatrix(newSize);
int** B11 = allocateMatrix(newSize);
int** B12 = allocateMatrix(newSize);
int** B21 = allocateMatrix(newSize);
int** B22 = allocateMatrix(newSize);
int** C11 = allocateMatrix(newSize);
int** C12 = allocateMatrix(newSize);
int** C21 = allocateMatrix(newSize);
int** C22 = allocateMatrix(newSize);
int** P1 = allocateMatrix(newSize);
int** P2 = allocateMatrix(newSize);
int** P3 = allocateMatrix(newSize);
int** P4 = allocateMatrix(newSize);
int** P5 = allocateMatrix(newSize);
int** P6 = allocateMatrix(newSize);
int** P7 = allocateMatrix(newSize);
// Dividing matrices into submatrices
for (int i = 0; i < newSize; i++) {
for (int j = 0; j < newSize; j++) {
A11[i][j] = A[i][j];
A12[i][j] = A[i][j + newSize];
A21[i][j] = A[i + newSize][j];
A22[i][j] = A[i + newSize][j + newSize];
B11[i][j] = B[i][j];
B12[i][j] = B[i][j + newSize];
B21[i][j] = B[i + newSize][j];
B22[i][j] = B[i + newSize][j + newSize];
}
}
// Recursive calls
strassenMultiplication(A11, B11, P1, newSize);
strassenMultiplication(A12, B21, P2, newSize);
strassenMultiplication(A11, B12, P3, newSize);
strassenMultiplication(A12, B22, P4, newSize);
strassenMultiplication(A21, B11, P5, newSize);
strassenMultiplication(A22, B21, P6, newSize);
strassenMultiplication(A21, B12, P7, newSize);
// Calculating submatrices of C using Strassen’s formulas
addMatrix(P1, P2, C11, newSize);
addMatrix(P3, P4, C12, newSize);
addMatrix(P5, P6, C21, newSize);
addMatrix(P4, P5, P4, newSize);
addMatrix(P4, P7, P4, newSize);
subtractMatrix(C11, P4, C11, newSize);
subtractMatrix(C11, P6, C22, newSize);
addMatrix(P3, P5, C12, newSize);
addMatrix(P2, P4, C21, newSize);
// Combining submatrices to form the result matrix
for (int i = 0; i < newSize; i++) {
for (int j = 0; j < newSize; j++) {
C[i][j] = C11[i][j];
C[i][j + newSize] = C12[i][j];
C[i + newSize][j] = C21[i][j];
C[i + newSize][j + newSize] = C22[i][j];
}
}
// Deallocating submatrices
deallocateMatrix(A11, newSize);
deallocateMatrix(A12, newSize);
deallocateMatrix(A21, newSize);
deallocateMatrix(A22, newSize);
deallocateMatrix(B11, newSize);
deallocateMatrix(B12, newSize);
deallocateMatrix(B21, newSize);
deallocateMatrix(B22, newSize);
deallocateMatrix(C11, newSize);
deallocateMatrix(C12, newSize);
deallocateMatrix(C21, newSize);
deallocateMatrix(C22, newSize);
deallocateMatrix(P1, newSize);
deallocateMatrix(P2, newSize);
deallocateMatrix(P3, newSize);
deallocateMatrix(P4, newSize);
deallocateMatrix(P5, newSize);
deallocateMatrix(P6, newSize);
deallocateMatrix(P7, newSize);
}
// Function to display a matrix
void displayMatrix(int** matrix, int size) {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
printf(“%d “, matrix[i][j]);
}
printf(“\n”);
}
}
// Main function
int main() {
int size = 4; // Size of the matrices
// Example matrices A, B, and C
int** A = allocateMatrix(size);
int** B = allocateMatrix(size);
int** C = allocateMatrix(size);
// Initializing matrices A(4×4) and B(4×4)
A[0][0] = 1;
A[0][1] = 2;
A[0][2] = 3;
A[0][3] = 4;
A[1][0] = 5;
A[1][1] = 6;
A[1][2] = 7;
A[1][3] = 8;
A[2][0] = 9;
A[2][1] = 10;
A[2][2] = 11;
A[2][3] = 12;
A[3][0] = 13;
A[3][1] = 14;
A[3][2] = 15;
A[3][3] = 16;
B[0][0] = 1;
B[0][1] = 2;
B[0][2] = 3;
B[0][3] = 4;
B[1][0] = 5;
B[1][1] = 6;
B[1][2] = 7;
B[1][3] = 8;
B[2][0] = 9;
B[2][1] = 10;
B[2][2] = 11;
B[2][3] = 12;
B[3][0] = 13;
B[3][1] = 14;
B[3][2] = 15;
B[3][3] = 16;
printf(“Matrix A:\n”);
displayMatrix(A, size);
printf(“\nMatrix B:\n”);
displayMatrix(B, size);
// Performing matrix multiplication using Strassen’s Algorithm
strassenMultiplication(A, B, C, size);
printf(“\nResultant Matrix C:\n”);
displayMatrix(C, size);
// Deallocating matrices
deallocateMatrix(A, size);
deallocateMatrix(B, size);
deallocateMatrix(C, size);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a Program to multiply two matrices from Strassen’s Algorithm
#include <iostream>
#include <cstdlib>
using namespace std;
// Function to allocate memory for a matrix
int** allocateMatrix(int size) {
int** matrix = new int*[size];
for (int i = 0; i < size; i++)
matrix[i] = new int[size];
return matrix;
}
// Function to deallocate memory of a matrix
void deallocateMatrix(int** matrix, int size) {
for (int i = 0; i < size; i++)
delete[] matrix[i];
delete[] matrix;
}
// Function to add two matrices
void addMatrix(int** A, int** B, int** C, int size) {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
C[i][j] = A[i][j] + B[i][j];
}
}
}
// Function to subtract two matrices
void subtractMatrix(int** A, int** B, int** C, int size) {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
C[i][j] = A[i][j] – B[i][j];
}
}
}
// Function to multiply two matrices using Strassen’s Algorithm
void strassenMultiplication(int** A, int** B, int** C, int size) {
if (size <= 4) {
// Base case: Use naive matrix multiplication for small matrices
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
C[i][j] = 0;
for (int k = 0; k < size; k++) {
C[i][j] += A[i][k] * B[k][j];
}
}
}
return;
}
int newSize = size / 2;
// Creating submatrices
int** A11 = allocateMatrix(newSize);
int** A12 = allocateMatrix(newSize);
int** A21 = allocateMatrix(newSize);
int** A22 = allocateMatrix(newSize);
int** B11 = allocateMatrix(newSize);
int** B12 = allocateMatrix(newSize);
int** B21 = allocateMatrix(newSize);
int** B22 = allocateMatrix(newSize);
int** C11 = allocateMatrix(newSize);
int** C12 = allocateMatrix(newSize);
int** C21 = allocateMatrix(newSize);
int** C22 = allocateMatrix(newSize);
int** P1 = allocateMatrix(newSize);
int** P2 = allocateMatrix(newSize);
int** P3 = allocateMatrix(newSize);
int** P4 = allocateMatrix(newSize);
int** P5 = allocateMatrix(newSize);
int** P6 = allocateMatrix(newSize);
int** P7 = allocateMatrix(newSize);
// Dividing matrices into submatrices
for (int i = 0; i < newSize; i++) {
for (int j = 0; j < newSize; j++) {
A11[i][j] = A[i][j];
A12[i][j] = A[i][j + newSize];
A21[i][j] = A[i + newSize][j];
A22[i][j] = A[i + newSize][j + newSize];
B11[i][j] = B[i][j];
B12[i][j] = B[i][j + newSize];
B21[i][j] = B[i + newSize][j];
B22[i][j] = B[i + newSize][j + newSize];
}
}
// Recursive calls
strassenMultiplication(A11, B11, P1, newSize);
strassenMultiplication(A12, B21, P2, newSize);
strassenMultiplication(A11, B12, P3, newSize);
strassenMultiplication(A12, B22, P4, newSize);
strassenMultiplication(A21, B11, P5, newSize);
strassenMultiplication(A22, B21, P6, newSize);
strassenMultiplication(A21, B12, P7, newSize);
// Calculating submatrices of C using Strassen’s formulas
addMatrix(P1, P2, C11, newSize);
addMatrix(P3, P4, C12, newSize);
addMatrix(P5, P6, C21, newSize);
addMatrix(P4, P5, P4, newSize);
addMatrix(P4, P7, P4, newSize);
subtractMatrix(C11, P4, C11, newSize);
subtractMatrix(C11, P6, C22, newSize);
addMatrix(P3, P5, C12, newSize);
addMatrix(P2, P4, C21, newSize);
// Combining submatrices to form the result matrix
for (int i = 0; i < newSize; i++) {
for (int j = 0; j < newSize; j++) {
C[i][j] = C11[i][j];
C[i][j + newSize] = C12[i][j];
C[i + newSize][j] = C21[i][j];
C[i + newSize][j + newSize] = C22[i][j];
}
}
// Deallocating submatrices
deallocateMatrix(A11, newSize);
deallocateMatrix(A12, newSize);
deallocateMatrix(A21, newSize);
deallocateMatrix(A22, newSize);
deallocateMatrix(B11, newSize);
deallocateMatrix(B12, newSize);
deallocateMatrix(B21, newSize);
deallocateMatrix(B22, newSize);
deallocateMatrix(C11, newSize);
deallocateMatrix(C12, newSize);
deallocateMatrix(C21, newSize);
deallocateMatrix(C22, newSize);
deallocateMatrix(P1, newSize);
deallocateMatrix(P2, newSize);
deallocateMatrix(P3, newSize);
deallocateMatrix(P4, newSize);
deallocateMatrix(P5, newSize);
deallocateMatrix(P6, newSize);
deallocateMatrix(P7, newSize);
}
// Function to display a matrix
void displayMatrix(int** matrix, int size) {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
cout << matrix[i][j] << ” “;
}
cout << endl;
}
}
// Main function
int main() {
int size = 4; // Size of the matrices
// Example matrices A, B, and C
int** A = allocateMatrix(size);
int** B = allocateMatrix(size);
int** C = allocateMatrix(size);
// Initializing matrices A(4×4) and B(4×4)
A[0][0] = 1;
A[0][1] = 2;
A[0][2] = 3;
A[0][3] = 4;
A[1][0] = 5;
A[1][1] = 6;
A[1][2] = 7;
A[1][3] = 8;
A[2][0] = 9;
A[2][1] = 10;
A[2][2] = 11;
A[2][3] = 12;
A[3][0] = 13;
A[3][1] = 14;
A[3][2] = 15;
A[3][3] = 16;
B[0][0] = 1;
B[0][1] = 2;
B[0][2] = 3;
B[0][3] = 4;
B[1][0] = 5;
B[1][1] = 6;
B[1][2] = 7;
B[1][3] = 8;
B[2][0] = 9;
B[2][1] = 10;
B[2][2] = 11;
B[2][3] = 12;
B[3][0] = 13;
B[3][1] = 14;
B[3][2] = 15;
B[3][3] = 16;
cout << “Matrix A:” << endl;
displayMatrix(A, size);
cout << endl << “Matrix B:” << endl;
displayMatrix(B, size);
// Performing matrix multiplication using Strassen’s Algorithm
strassenMultiplication(A, B, C, size);
cout << endl << “Resultant Matrix C:” << endl;
displayMatrix(C, size);
// Deallocating matrices
deallocateMatrix(A, size);
deallocateMatrix(B, size);
deallocateMatrix(C, size);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a Program to multiply two matrices from Strassen’s Algorithm
public class StrassenMatrixMultiplication {
// Function to allocate memory for a matrix
public static int[][] allocateMatrix(int size) {
return new int[size][size];
}
// Function to add two matrices
public static int[][] addMatrix(int[][] A, int[][] B, int size) {
int[][] C = new int[size][size];
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
C[i][j] = A[i][j] + B[i][j];
}
}
return C;
}
// Function to subtract two matrices
public static int[][] subtractMatrix(int[][] A, int[][] B, int size) {
int[][] C = new int[size][size];
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
C[i][j] = A[i][j] – B[i][j];
}
}
return C;
}
// Function to multiply two matrices using Strassen’s Algorithm
public static int[][] strassenMultiplication(int[][] A, int[][] B, int size) {
if (size <= 4) {
// Base case: Use naive matrix multiplication for small matrices
int[][] C = new int[size][size];
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
C[i][j] = 0;
for (int k = 0; k < size; k++) {
C[i][j] += A[i][k] * B[k][j];
}
}
}
return C;
}
int newSize = size / 2;
// Creating submatrices
int[][] A11 = new int[newSize][newSize];
int[][] A12 = new int[newSize][newSize];
int[][] A21 = new int[newSize][newSize];
int[][] A22 = new int[newSize][newSize];
int[][] B11 = new int[newSize][newSize];
int[][] B12 = new int[newSize][newSize];
int[][] B21 = new int[newSize][newSize];
int[][] B22 = new int[newSize][newSize];
// Dividing matrices into submatrices
for (int i = 0; i < newSize; i++) {
for (int j = 0; j < newSize; j++) {
A11[i][j] = A[i][j];
A12[i][j] = A[i][j + newSize];
A21[i][j] = A[i + newSize][j];
A22[i][j] = A[i + newSize][j + newSize];
B11[i][j] = B[i][j];
B12[i][j] = B[i][j + newSize];
B21[i][j] = B[i + newSize][j];
B22[i][j] = B[i + newSize][j + newSize];
}
}
// Recursive calls
int[][] P1 = strassenMultiplication(A11, subtractMatrix(B12, B22, newSize), newSize);
int[][] P2 = strassenMultiplication(addMatrix(A11, A12, newSize), B22, newSize);
int[][] P3 = strassenMultiplication(addMatrix(A21, A22, newSize), B11, newSize);
int[][] P4 = strassenMultiplication(A22, subtractMatrix(B21, B11, newSize), newSize);
int[][] P5 = strassenMultiplication(addMatrix(A11, A22, newSize), addMatrix(B11, B22, newSize), newSize);
int[][] P6 = strassenMultiplication(subtractMatrix(A12, A22, newSize), addMatrix(B21, B22, newSize), newSize);
int[][] P7 = strassenMultiplication(subtractMatrix(A11, A21, newSize), addMatrix(B11, B12, newSize), newSize);
// Calculating submatrices of C using Strassen’s formulas
int[][] C11 = subtractMatrix(addMatrix(addMatrix(P5, P4, newSize), P6, newSize), P2, newSize);
int[][] C12 = addMatrix(P1, P2, newSize);
int[][] C21 = addMatrix(P3, P4, newSize);
int[][] C22 = subtractMatrix(subtractMatrix(addMatrix(P5, P1, newSize), P3, newSize), P7, newSize);
// Combining submatrices to form the result matrix
int[][] C = new int[size][size];
for (int i = 0; i < newSize; i++) {
for (int j = 0; j < newSize; j++) {
C[i][j] = C11[i][j];
C[i][j + newSize] = C12[i][j];
C[i + newSize][j] = C21[i][j];
C[i + newSize][j + newSize] = C22[i][j];
}
}
return C;
}
// Function to display a matrix
public static void displayMatrix(int[][] matrix, int size) {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
System.out.print(matrix[i][j] + ” “);
}
System.out.println();
}
}
// Main function
public static void main(String[] args) {
int size = 4; // Size of the matrices
// Example matrices A, B, and C
int[][] A = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12},
{13, 14, 15, 16}
};
int[][] B = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12},
{13, 14, 15, 16}
};
int[][] C;
System.out.println(“Matrix A:”);
displayMatrix(A, size);
System.out.println(“\nMatrix B:”);
displayMatrix(B, size);
// Performing matrix multiplication using Strassen’s Algorithm
C = strassenMultiplication(A, B, size);
System.out.println(“\nResultant Matrix C:”);
displayMatrix(C, size);
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a Program to multiply two matrices from Strassen’s Algorithm
def allocate_matrix(size):
return [[0 for _ in range(size)] for _ in range(size)]
def add_matrix(A, B, size):
C = allocate_matrix(size)
for i in range(size):
for j in range(size):
C[i][j] = A[i][j] + B[i][j]
return C
def subtract_matrix(A, B, size):
C = allocate_matrix(size)
for i in range(size):
for j in range(size):
C[i][j] = A[i][j] – B[i][j]
return C
def strassen_multiplication(A, B, size):
if size <= 4:
# Base case: Use naive matrix multiplication for small matrices
C = allocate_matrix(size)
for i in range(size):
for j in range(size):
C[i][j] = sum(A[i][k] * B[k][j] for k in range(size))
return C
new_size = size // 2
# Creating submatrices
A11 = [[A[i][j] for j in range(new_size)] for i in range(new_size)]
A12 = [[A[i][j + new_size] for j in range(new_size)] for i in range(new_size)]
A21 = [[A[i + new_size][j] for j in range(new_size)] for i in range(new_size)]
A22 = [[A[i + new_size][j + new_size] for j in range(new_size)] for i in range(new_size)]
B11 = [[B[i][j] for j in range(new_size)] for i in range(new_size)]
B12 = [[B[i][j + new_size] for j in range(new_size)] for i in range(new_size)]
B21 = [[B[i + new_size][j] for j in range(new_size)] for i in range(new_size)]
B22 = [[B[i + new_size][j + new_size] for j in range(new_size)] for i in range(new_size)]
# Recursive calls
P1 = strassen_multiplication(A11, subtract_matrix(B12, B22, new_size), new_size)
P2 = strassen_multiplication(add_matrix(A11, A12, new_size), B22, new_size)
P3 = strassen_multiplication(add_matrix(A21, A22, new_size), B11, new_size)
P4 = strassen_multiplication(A22, subtract_matrix(B21, B11, new_size), new_size)
P5 = strassen_multiplication(add_matrix(A11, A22, new_size), add_matrix(B11, B22, new_size), new_size)
P6 = strassen_multiplication(subtract_matrix(A12, A22, new_size), add_matrix(B21, B22, new_size), new_size)
P7 = strassen_multiplication(subtract_matrix(A11, A21, new_size), add_matrix(B11, B12, new_size), new_size)
# Calculating submatrices of C using Strassen’s formulas
C11 = subtract_matrix(add_matrix(add_matrix(P5, P4, new_size), P6, new_size), P2, new_size)
C12 = add_matrix(P1, P2, new_size)
C21 = add_matrix(P3, P4, new_size)
C22 = subtract_matrix(subtract_matrix(add_matrix(P5, P1, new_size), P3, new_size), P7, new_size)
# Combining submatrices to form the result matrix
C = allocate_matrix(size)
for i in range(new_size):
for j in range(new_size):
C[i][j] = C11[i][j]
C[i][j + new_size] = C12[i][j]
C[i + new_size][j] = C21[i][j]
C[i + new_size][j + new_size] = C22[i][j]
return C
def display_matrix(matrix, size):
for i in range(size):
for j in range(size):
print(matrix[i][j], end=” “)
print()
# Main function
if __name__ == “__main__”:
size = 4 # Size of the matrices
# Example matrices A, B, and C
A = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]
]
B = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]
]
print(“Matrix A:”)
display_matrix(A, size)
print(“\nMatrix B:”)
display_matrix(B, size)
# Performing matrix multiplication using Strassen’s Algorithm
C = strassen_multiplication(A, B, size)
print(“\nResultant Matrix C:”)
display_matrix(C, size)
Advantage of Strassen’s Algorithm
- Strassen’s algorithm has a lower asymptotic complexity compared to the traditional matrix multiplication algorithm.
- Strassen’s algorithm performs well for large matrices due to its recursive nature. By dividing the matrices into smaller submatrices and recursively applying the algorithm, it reduces the overall number of multiplications required.
Disadvantage of Strassen’s Algorithm
- Increased Overhead
- Precision and Rounding Errors
- Memory Usage for product.
- Not Suitable for Irregular Matrices. Strassen’s algorithm assumes that the input matrices have dimensions that are powers of 2.
Also, It is just for the computers. Humans always use the traditional method because it is simple. Humans want convenience and therefore use the traditional method.
Applications of Strassen’s Multiplication
- Scientific Computing
- Image filtering, compression, and pattern recognition
- Machine Learning and Data Analysis.
- Speed up cryptography.
- Parallel and Distributed Computing.
Test Yourself
Q1- Explain the concept of Strassen’s Algorithm and how it improves matrix multiplication efficiency.
Strassen’s Algorithm is a divide-and-conquer approach that reduces the number of multiplications needed to compute the matrix product. By breaking down the matrices into smaller submatrices and using specific equations to combine intermediate results, it reduces the time complexity to approximately O(n^log2(7)). This optimization improves the efficiency of matrix multiplication compared to traditional algorithms.
Q2- Discuss the limitations and considerations of Strassen’s Algorithm.
The algorithm performs better for larger matrices, but the initial stages may be slower than traditional multiplication. Additionally, it requires the input matrices to have dimensions that are powers of 2, and precision and rounding errors can occur due to floating-point arithmetic.
Also, It is just for the computers. Humans always use the traditional method because it is simple.
Humans want convenience and therefore use the traditional method.
Q3- How does Strassen’s Algorithm achieve a reduction in the number of multiplications?
Strassen’s Algorithm combines seven multiplications in each recursive step, instead of the traditional eight multiplications. By strategically computing intermediate matrix products and applying addition and subtraction operations, it intelligently reduces the overall number of multiplications required.
Q4- Describe the recursive nature of Strassen’s Algorithm.
Strassen’s Algorithm uses a recursive divide-and-conquer strategy. It breaks down the input matrices into smaller submatrices, each with dimensions halved, and applies the algorithm recursively until the base case is reached (typically 1×1 matrices).
Q5- Can Strassen’s Algorithm be applied to matrices with non-power-of-2 dimensions?
Strassen’s Algorithm assumes that the input matrices have dimensions that are powers of 2. Therefore, it may not directly apply to matrices with non-power-of-2 dimensions without additional preprocessing steps to adjust the dimensions.
Q6- What is the main advantage of Strassen’s Algorithm?
Reduced memory usage
Faster for small matrices
Improved efficiency for large matrices
Simplicity of implementation
Ans – (3)
Explanation – Strassen’s Algorithm provides better efficiency for large matrices due to its recursive nature and reduction in the number of multiplications.
Q7- What type of matrices does Strassen’s Algorithm require as input?
Matrices with any dimensions
Matrices with dimensions that are powers of 2
Matrices with prime dimensions
Matrices with equal dimensions
Ans – (2)
Explanation – Strassen’s Algorithm assumes that the input matrices have dimensions that are powers of 2 to ensure proper recursive subdivision.
Q8- Which step of Strassen’s Algorithm involves combining intermediate matrix products?
Divide the input matrices
Recursive computation of intermediate matrices
Merge submatrices to form the final output
Compute intermediate matrix products using specific equations
Ans – (3)
Explanation – The final step of Strassen’s Algorithm involves merging the intermediate matrices obtained from the recursive calls to obtain the final output matrix.
Q9- What is the main limitation of Strassen’s Algorithm?
Higher memory usage
Limited applicability to small matrices
Inability to handle non-square matrices
Precision and rounding errors
Ans – (4)
Explanation – Strassen’s Algorithm, like any floating-point arithmetic, can introduce precision and rounding errors due to the nature of the calculations involved.
Q10- Which traditional algorithm does Strassen’s Algorithm improve upon?
Bubble sort
Quick sort
Matrix addition
Matrix multiplication
Ans – (4)
Explanation – Strassen’s Algorithm is an optimization for matrix multiplication, improving the efficiency of this operation compared to traditional algorithms.
Q11- What is the main advantage of Strassen’s Algorithm in scientific computing applications?
Higher precision of results
Ability to handle irregular matrices
Reduced computational complexity
Improved parallelization potential
Ans – (4)
Explanation – Strassen’s Algorithm’s recursive nature and reduced number of multiplications allow for easier parallelization, which is beneficial in scientific computing applications.
Q12- What is the base case in Strassen’s Algorithm?
Matrices with dimensions 1×1
Matrices with dimensions 2×2
Matrices with dimensions 3×3
Matrices with dimensions 4×4
Ans – (1)
Explanation – The base case in Strassen’s Algorithm is typically reached when the input matrices are reduced to 1×1 size, and direct multiplication can be performed.
Q13- Which operation is NOT involved in Strassen’s Algorithm?
Matrix addition
Matrix subtraction
Matrix division
Matrix multiplication
Ans – (3)
Explanation – Strassen’s Algorithm uses matrix addition, subtraction, and multiplication, but it does not involve matrix division.
Q14- What is the main trade-off of using Strassen’s Algorithm?
Higher memory usage
Slower execution for small matrices
Inaccuracy in results
Difficulty in implementation
Ans – (1)
Explanation – Strassen’s Algorithm requires additional memory to store the submatrices and intermediate results, which can result in higher memory usage compared to traditional matrix multiplication algorithms.






