Unit 2
Sorting:- Type of Sorting, Bubble Sort, Selection Sort, Insertion Sort, Binary Insertion Sort, Shell Sort, Quick Sort, Merge Sort, Heap, Heap Sort. Sorting in Linear Time:- Counting Sort, Radix Sort, Bucket Sort.
Q41 – Input – 82, 90, 10, 11, 15, 78, 55, 24. We apply Max heap property, then the output would be
90, 82, 55, 24, 15, 10, 78, 11
90, 82, 78, 24, 11, 10, 55, 15
90, 82, 78, 24, 15, 10, 55, 11
82, 90, 78, 24, 15, 10, 55, 11
Ans – (3)
Explanation – If the parent node is stored at index I, the left child can be calculated by 2 * I + 1 and the right child by 2 * I + 2 (assuming the indexing starts at 0).
Q42 – Input – 3, 2, 4, 1, 5 Output – 1, 2, 3, 4, 5. How many iterations does bubble sort take
Two
Four
Five
Three
Ans – (4)
Explanation –
First iteration – 2, 3, 1, 4, 5
Second iteration – 2, 1, 3, 4, 5
Third iteration – 1, 2, 3, 4, 5
Q43 – Which one of the following array represents a binary max heap?
{25, 12, 16, 13, 10, 8, 4}
{25, 14, 13, 16, 10, 8, 12}
{25, 14, 16, 13, 10, 8, 12}
{25, 14, 12, 13, 10, 8, 16}
Ans – (3)
Explanation – The root node value in Max-heap is greater than or equal to every child node value.
If i variable represents the index, then a[i] ≥ a[2i+1] & a[2i+2]
Q44 – Quicksort algorithm is based on which algorithm design technique? (DSSSB PGT 2021)
Greedy Algorithm
Brute – Force
Dynamic programing
Divide and Conquer
Ans – (4)
Explanation – The Quicksort algorithm is based on the “Divide and Conquer” algorithm design technique. The divide and conquer strategy involve breaking down a problem into subproblems that are similar to the original problem, solving them recursively, and combining their solutions to obtain the solution to the original problem. In Quicksort, the algorithm recursively partitions an array into two subarrays, one with elements smaller than a chosen pivot and another with elements larger than the pivot, and then sorts these subarrays separately.
Q45 – How many interchanges will happen when the sequence of letters of “SORTED” is sorted using bubble sort? (DSSSB TGT 2021)
Ans – (3)
Explanation –
Bubble sort works by repeatedly swapping adjacent elements that are in the wrong order. In the first pass, the largest element is bubbled to the end of the list, in the second pass the second largest element is bubbled to the second-last position, and so on until the list is sorted.
For the sequence “SORTED”, the following interchanges will take place:
Pass 1: STORDE -> 1 interchange (T and S are swapped)
Pass 2: RSTODE -> 2 interchanges (R and S, O and R are swapped)
Pass 3: ORSTDE -> 2 interchanges (O and R, S and T are swapped)
Pass 4: ORSDET -> 2 interchanges (D and S, E and T are swapped)
Pass 5: DEROST -> 4 interchanges (D and E, E and O, O and R, S and T are swapped)
Therefore, the total number of interchanges is: 1 + 2 + 2 + 2 + 4 = 11 interchanges.
Q46 – What is the worst-case time complexity of bubble sort? (DSSSB TGT 2021, PGT 2018)
O(log2x)
O(x)
O(x2)
O(xlog2x)
Q47 – What is the worst-case time complexity of the heap sort? (DSSSB PGT 2018)
O(n)
O(n2)
O(n3)
O(nlogn)
Ans – (4)
Q48 – Which of the sorting algorithm has the worst-case time complexity of nlogn? (DSSSB TGT 2017)
Heap Sort
Quick Sort
Insertion Sort
Selection Sort
Ans – (1)
Explanation – In heap sort, we perform the deletion of a root and heapify the tree into a max-heap or min-heap in ‘log n’ time.
Suppose there are n nodes in a max-heap.
(i) The deletion of root and heapify the tree will take logn time.
(ii) Then, heap contains n-1 nodes, so the deletion of the second node and heapify tree will take log(n-1) time.
(iii) Then, heap contains n-2 nodes, so the deletion of the third node and heapify tree will take log(n-2) time.
(iv) After performing n-2 deletions, the second last item will take log 2 time.
(v) After performing n-1 deletions, the last item will take O(1) time.
-> Sum of all operations = log(n) + log(n-1) + log(n-2) + … + log2 + 1 = log(n!) = n*log(n) – n + log(n)
-> The time complexity is after taking higher order term is O(n*log(n)).
https://compgeek.co.in/heap-sort/ to know more.
Q49 – A sorting algorithm is called stable if (DSSSB TGT 2017) (ISRO Scientist 2017)
It takes O(nlogn) time
It maintains relative order of occurrence of non-distinct elements
It uses divide and conquer paradigm
It takes linear time
Ans – (2)
Explanation – Suppose before sorting, there are two numbers (ai and aj) same in the input and suppose i and j are their indexes, and i comes before j, then after sorting in the output, if ai comes before aj then you can say, it is a stable sort.
Q50 – Of the following sort algorithms, which has execution time that is least dependent on initial ordering of the input? (ISRO Scientist 2020 and 2018)
Insertion sort
Quick sort
Merge sort
Selection sort
Ans – (3)
Explanation – Merge sort has execution time that is independent on the initial ordering of system.
Merge sort is a divide-and-conquer algorithm that recursively breaks down a list into smaller sub-lists, sorts those sub-lists, and then merges them back together in the correct order.
Q51 – G is an undirected graph with vertex set {v1, v2, v3, v4, v5, v6, v7} and edge set {v1v2, v1v3, v1v4, v2v5, v3v4, v4v5, v4v6, v5v6, v6v7}. A breadth first search of the graph is performed with v1 as the root node. Which of the following is a tree edge? (ISRO SCIENTIST 2020)
v2v4
v1v4
v4v5
v3v4
Ans – (2)
Explanation – The graph is as follows –
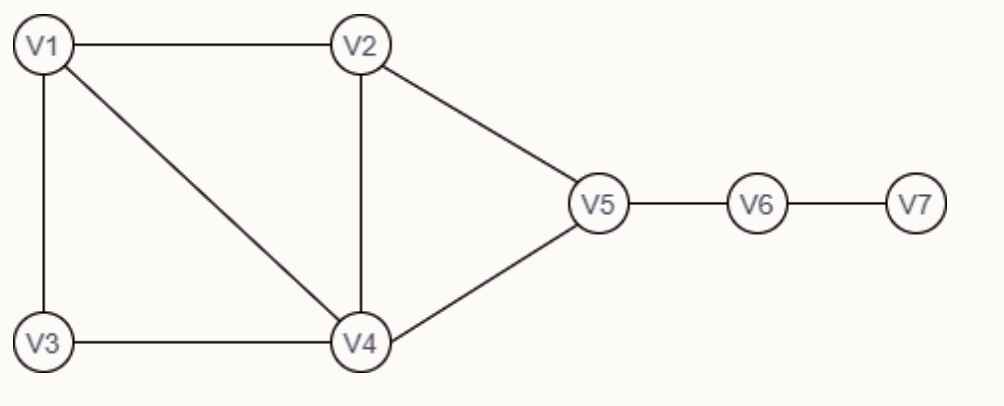
Breadth first search traversals
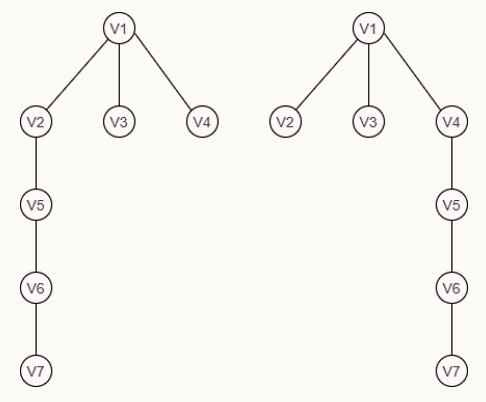
In this we cannot find tree edge v2v4 and v3v4. So these options are wrong. But we can see that v1v4 tree edge is present in both the trees and v4v5 can be seen only in the second tree. Hence option 2 is correct.
Q52 – If the array A contains the items 10, 4, 7, 23, 67, 12 and 5 in that order, what will be the resultant array A after third pass of insertion sort. (ISRO SCIENTIST 2020)
67, 12, 10, 5, 4, 7, 23
4, 7, 10, 23, 67, 12, 5
4, 5, 7, 67, 10, 12, 23
10, 7, 4, 67, 23, 12, 5
Ans – (2)
Explanation –
Input – 10, 4, 7, 23, 67, 12, 5
After 1st pass – 4, 10, 7, 23, 67, 12, 5
After 2nd pass – 4, 7, 10, 23, 67, 12, 5
After 3rd pass – 4, 7, 10, 23, 67, 12, 5
Q53 – Huffman tree is constructed for the following data: {A, B, C, D, E} with frequency {0.17, 0.11, 0.24, 0.33 and 0.15} respectively. 100 00 01101 is decoded as
BACE
CADE
BAD
CADD
Ans – (1)
Explanation – 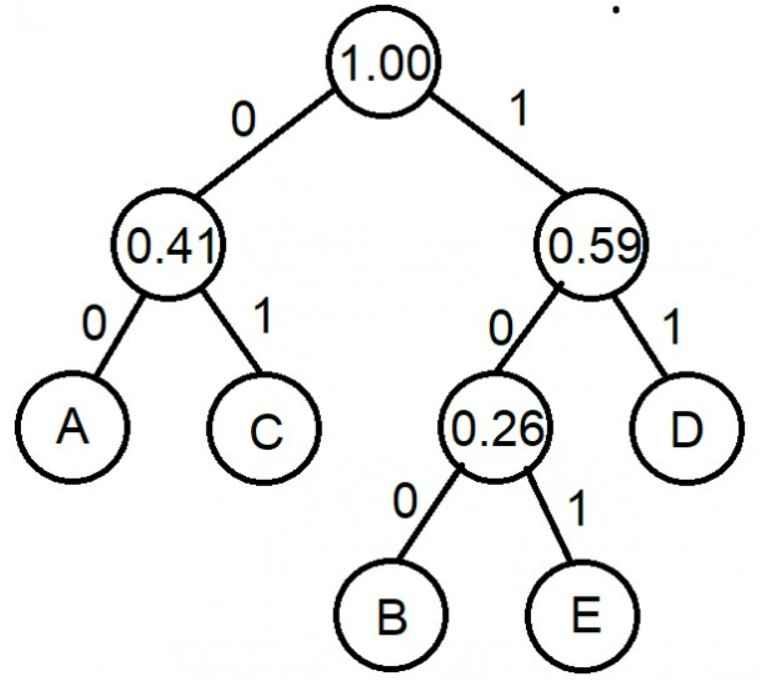
Q54 – Given two sorted list of size m and n respectively. The number of comparisons needed the worst case by the merge sort algorithm will be (ISRO Scientist 2018)
m*n
maximum of m and n
minimum of m and n
m+n-1
Ans – (4)
Explanation – The reason for this is that during the merging process, we compare the first element of each sub-list and choose the smaller one to add to the output list. We repeat this process until one of the sub-lists is completely processed, at which point we append the remaining elements of the other sub-list to the output list. Since the sub-lists are already sorted, the remaining elements of the non-empty list are larger than all the elements in the output list so far, and no more comparisons are needed.
Q55 – A has table with 10 buckets with one slot per bucket is depicted here. The symbols S1 to S7 are initially entered using a hashing function with linear probing. The maximum number of comparisons needed in searching an item that is not present is (ISRO Scientist 2018)
4
5
6
3
Ans – (2)
Explanation –
To determine the maximum number of comparisons required while looking for something that isn’t there, we must take into account several circumstances.
The maximum number of comparisons will also be necessary if searching begins at index 8, as in this example, a total of 5 comparisons will be done at index 8, 9, 0, 1 and 2.
Q56 – Given a binary max heap. The elements are sorted in an array as 25, 14, 16, 13, 10, 8, 12. What is the content of the array after two delete operations? (ISRO Scientist 2018)
14, 13, 8, 12, 10
14, 12, 13, 10, 8
14, 13, 12, 8, 10
14, 13, 12, 10, 8
Ans – (3)
Explanation –
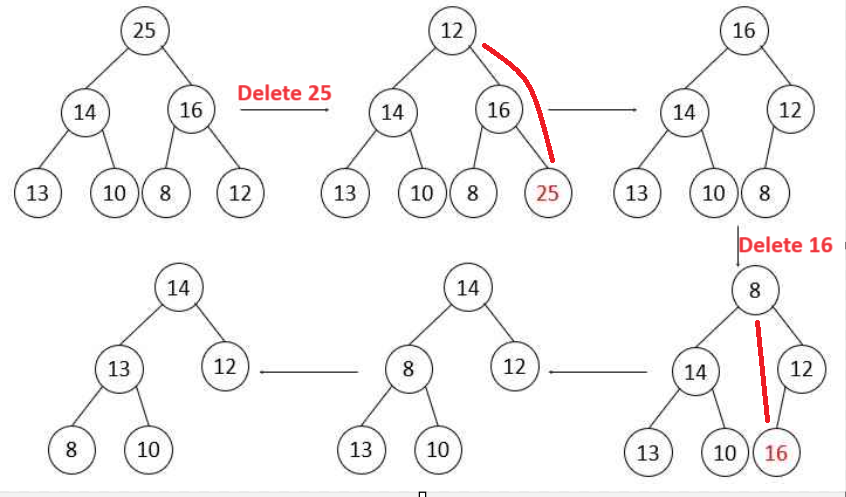
Q57 – Match the following and choose the correct answer in the order 1, 2, 3
Heap Construction
Hash table construction with linear probing
AVL Tree construction
p. O(nlogn)
q. O(n^2)
r. O(n)
(Bounds given may or may not be asymptotically tight) (ISRO Scientist 2017)
q, r, p
p, q, r
q, p, r
r, q, p
Ans – (4)
Let’s match the constructions with their time complexities:
Heap Construction: O(n) – Building a heap from an array can be done in linear time.
Hash Table Construction with Linear Probing: O(n^2) – In the worst-case scenario, linear probing for hash table construction may result in quadratic time complexity.
AVL Tree Construction: O(nlogn) – The AVL tree construction involves rotations to maintain the balance, resulting in logarithmic time complexity.
Matching the time complexities with the constructions, the correct order is:
r, q, p. The Answer is (4)
Q58 – Quick sort is run on 2 inputs shown below to sort in ascending order
A. 1, 2, 3……n
B. n, n – 1, n – 2 …… 1
Let C1 and C2 be the number of comparisons made for A and B respectively. (ISRO Scientist 2017)
C1 > C2
C1 = C2
C1 < C2
Cannot say anything for arbitrary n
Ans – (2)
Explanation – There are three cases when the worst case for Quick Sort arises:
(A) When the input array is already sorted in ascending or descending order.
(B) When the input array contains many duplicate elements, and the pivot is always chosen as one of the duplicate elements.
(C) When the input array contains all the same elements.
In all three cases, the recursive tree of Quick Sort degenerates into a skewed tree with n levels, where each level has only one node. Therefore, the time complexity of Quick Sort in the worst case becomes O(n^2). C1 comparisons is equal to C2 comparisons.
Q59 – A binary search tree is used to locate the number 43. Which one of the following probe sequences is not possible? (ISRO Scientist 2017)
61, 52, 14, 17, 40, 43
10, 65, 31, 48, 37, 43
81, 61, 52, 14, 41, 43
17, 77, 27, 66, 18, 43
Ans – (4)
Explanation –
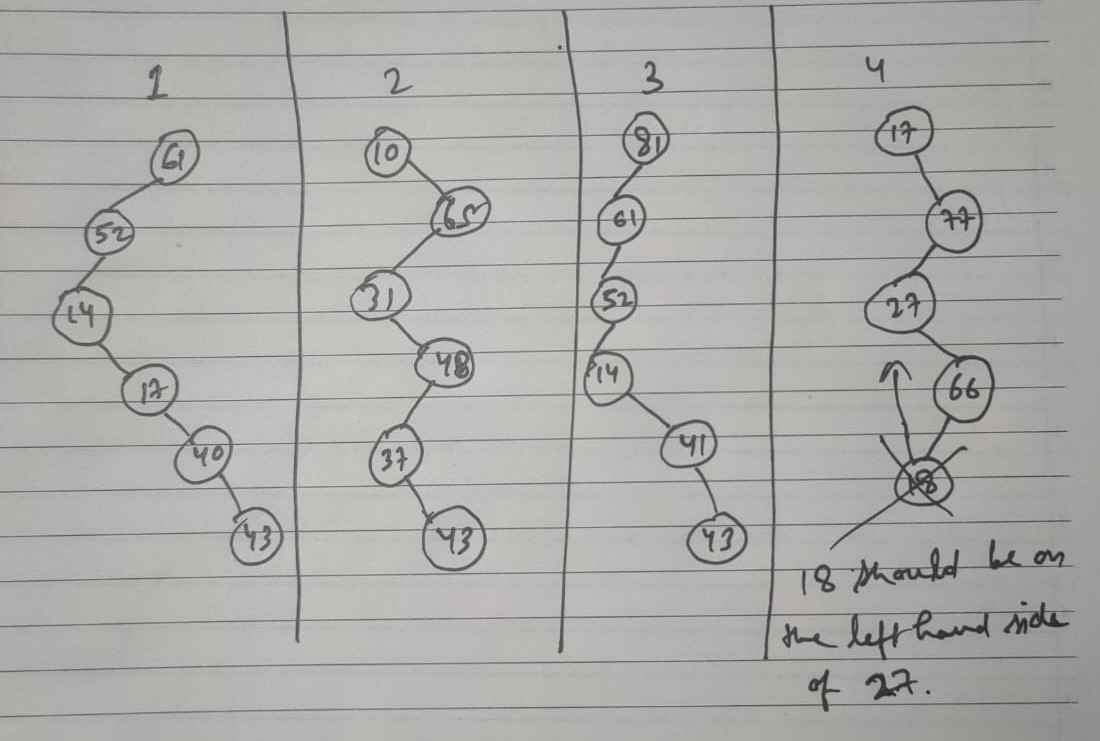
Q60 – Which one of the following in-place sorting algorithms needs the minimum number of
swaps? (ISRO Scientist 2017)
Insertion Sort
Quick Sort
Heap Sort
Selection Sort
Ans – (4)
Explanation –
Minimum number of swaps are in selection sort. In the worst case the maximum swaps are n-1.
Rest of all will swaps more than n-1.







