A red black tree is a self-balancing* binary search tree who have ‘colour’ as an extra attribute. The node is either red or black.
*Self-balancing binary search trees are height-balanced binary search trees.
In red-black tree, the node has five different attributes.
- Parent.
- Left child.
- Right child.
- Key (the number in the node).
- Color – Red or Black.
Red-black trees make sure that no simple path from the root to a leaf is longer than twice as long as any other path, so that the tree is always balanced by checking the node colors along that path.
These four requirements must be met by a red-black tree:
- The root node is always a black node.
- It is believed that a nil is black. (Figure 1)
- Every red node has black children.
- The equal number of black nodes appear on each path from the root to the leaf nodes.
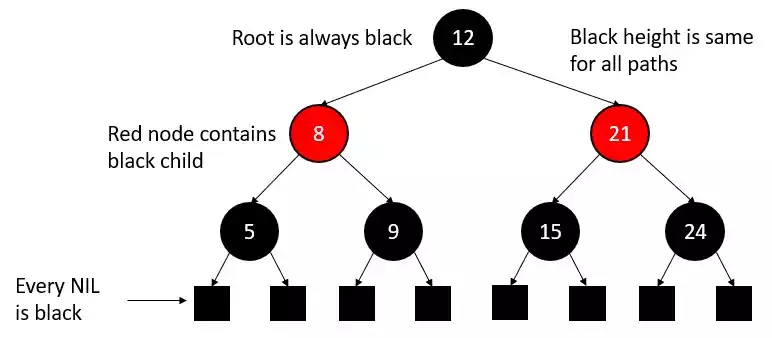
A NIL is a square node with every leaf that is always thought of as black and can be forgettable. So, we will use the diagram with no NIL nodes in the future.
.
History
Rudolf Bayer created a data structure in 1972 that was a special order-4 B-tree instance.
These trees produced perfectly balanced trees by keeping the same number of nodes along every path from root to leaf. They weren’t binary search trees, though. They gained popularity as 2–3–4 trees or even 2–4 trees when Bayer referred to them as a “symmetric binary B-tree” in his article.
The red-black tree was derived from the symmetric binary B-tree by Leonidas J. Guibas and Robert Sedgewick in their 1978 publication “A Dichromatic Framework for Balanced Trees“. The authors selected the color “red” because, during their time at Xerox PARC, they found that it looked the best when printed on a color laser printer.
According to Guibas, the reason behind it was the red and black pens they had on hand for drawing the trees.
.
Operations in Red Black Trees
When we conduct certain insertions or deletions in the red black tree, the result violates the property of the red-black tree. To recover these properties, we simply modify the colors of some of the tree’s nodes as well as the pointer structure.
Rotation changes the pointer structure. You have encountered the rotation into AVL trees. In this red black tree, two operations can be done
1. Recolor (Red to black or Black to red)
2. Rotation (As we saw in the AVL trees)
- Left rotation
- Right rotation
- Left-right rotation
- Right-left rotation
Note – First, you have to recolor it because that saves time. Do not rotate the tree until you have tried recoloring. If recoloring doesn’t work, then rotation is the only option.
Some basic operations in the Red Black Tree are
- Insertion
- Delete
1. Insertion
Suppose a red-black tree is there, and we will do an insertion into the tree. The insertion of a new node will generate a new leaf.
After doing the insertion, we have to color it, and if the tree’s black height is unbalanced, we have to rotate it.
For example – Insert the elements 8, 20, 11, 14, 9, 4, 12 in a red black tree. (IPU 2017-18) (AKTU 2018-19) (Marks 07)
Insert 8
If the tree is an empty tree, then make node 8 as the root and color it black.

All four properties of red black tree met.
Insert 20
20 > 8, so node 20 will be the right child of node 8 and its color is red.
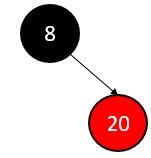
All four properties of red black tree met.
Insert 11
11 < 20, so node 11 will be the left child of node 20 and its color is red.
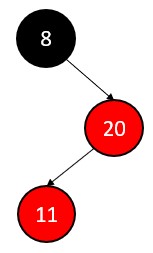
Property Every red node has black children, but here 20 is a red parent having left child red 11.
But recoloring is not possible, as the property of black height will violate. All we have to do is Right-left rotation.
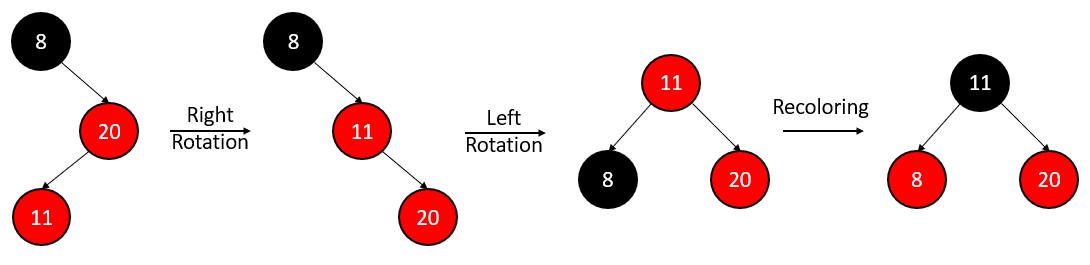
All four properties of red black tree met.
Insert 14
14 < 20, so node 14 will be the left child of node 8 and its color is red.
The property “every red node has black children” is violated. So, recolor the node 8 and node 20 black.
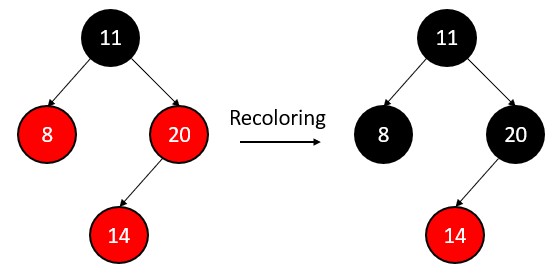
All four properties of red black tree met.
Insert 9
9 > 8, so node 9 will be the right child of node 8 and its colour is red.

All four properties of red black tree met.
Insert 4

All four properties of red black tree met.
Insert 12
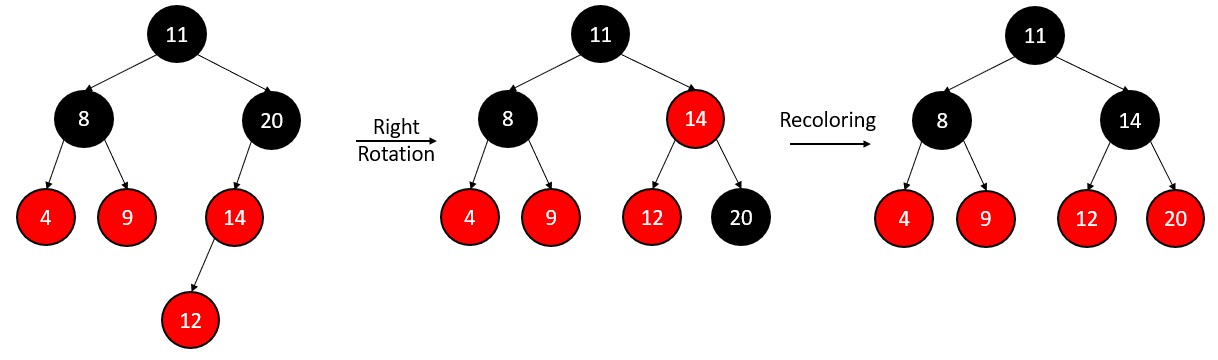
All four properties of red black tree met.
.
2. Deletion
If you delete a node in the red black tree, you may violate the previously specified property. We recolor the tree nodes to match all properties, and if that doesn’t work, we rotate them.
To delete a node n, identify its predecessor in the left subtree and replace it with the deleted node.
Input is –
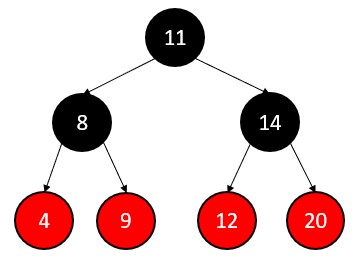
Delete 12
Node 12 has neither a predecessor nor a successor because it has no children. So, delete this node and verify all the properties are met after deletion.
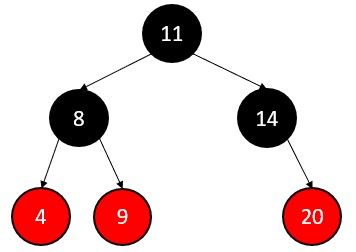
All four properties of red black tree met after deletion.
Delete 14
Node 14 has the right child. It has no predecessor, but it has a successor, 20. Its parent node 11 will become the parent of its child node 20. Because 20 is red, it violates the same black height as every path. After recoloring, node 20 will be a black node, and all four conditions of the red-black tree will be met.

Delete 11
Node 11 has both children. So, find the predecessor in the left subtree of the node.
The predecessor is 9. So, replace the node 11 by node 9 and color it black, because 11 is the root node of the tree.
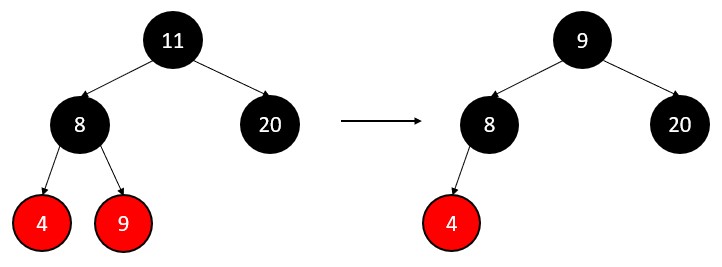
After deletion, all four properties of the red-black tree are met.
Time & Space Complexity of Red-Black Tree
- The searching of a node in the red black tree is O(log n) where n is the number of nodes. It’s because this is a height-balanced tree.
- Insertion and deletion of a node in the red black tree costs O(log n). Whereas, the whole tree insertion and deletion costs O(n*log n).
- Space complexity of red black tree will be O(n) because in each node, we store its color either red or black.
Advantages
- These operations are guaranteed to be O(log(n)) since red-black trees are self-balancing.
- Inserts and deletions happen rapidly.
Disadvantages
- It is very difficult when color has to be filled in this tree.
Applications
- They are employed in scheduling algorithms to manage tasks efficiently, ensuring balanced scheduling and quick access to upcoming events.
- Red-Black trees are used in network routing tables to efficiently search for destinations, optimizing data transmission in computer networks.
- They are utilized in implementing transactional databases, ensuring efficient indexing and retrieval of data while maintaining ACID properties.
- Red-Black trees are used in compiler implementations for symbol table management, facilitating fast lookups of identifiers during parsing.
- They are used in balanced tree data structures, such as interval trees, for efficient storage and retrieval of overlapping intervals in applications like calendar systems.
- Red-Black trees find applications in garbage collection algorithms to efficiently manage memory allocation and deallocation in programming languages.
- They are employed in spell-checking algorithms to quickly search for and suggest corrections for misspelled words in text processing applications.
Test Yourself
Q1- What is a Red-Black Tree, and what are its key properties?
A Red-Black Tree is a self-balancing binary search tree in which each node has an extra attribute called “color,” which can be either red or black. The key properties of a Red-Black Tree are as follows:
- The root node is always black.
- Every leaf (NULL node) is considered black.
- Red nodes cannot have red children; they can only have black children.
- All simple paths from any node to its descendant leaves must have an equal number of black nodes, ensuring that the tree is balanced.
Q2- How do Red-Black Trees maintain their balanced property after insertions and deletions?
Red-Black Trees maintain their balanced property through recoloring and rotations.
When a new node is inserted, its color is initially set to red, and then the tree’s properties are checked. If any property is violated, the tree is restructured through recoloring and rotations to ensure that it remains balanced.
Similarly, during deletions, the tree is adjusted using recoloring and rotations to maintain the balance property.
Q3- Explain the concept of recoloring in a Red-Black Tree and when it is used.
Recoloring in a Red-Black Tree involves changing the color of nodes to ensure that the tree remains balanced. It is used when inserting or deleting a node in the tree violates the Red-Black Tree properties.
For example, when a red node has red children, recoloring can be applied to convert one of the red children to black, thereby restoring the balance.
Q4- What are the possible rotations in a Red-Black Tree, and when are they applied?
There are four possible rotations in a Red-Black Tree:
i. Left Rotation
ii. Right Rotation
iii. Left-Right (LR) Rotation
iv. Right-Left (RL) Rotation
These rotations are applied when the tree becomes unbalanced due to insertions or deletions, and recoloring alone cannot restore the balance. Rotations change the pointer structure of the tree, maintaining the Red-Black Tree properties while ensuring it remains balanced.
Q5- How are insertions handled in a Red-Black tree, and what operations are performed to maintain balance?
When a new node is inserted into a Red-Black tree, it is initially colored red. After insertion, the tree may become unbalanced, violating the Red-Black tree properties. To maintain balance, two operations are considered:
i. Recoloring – Attempt to change the colors of some nodes to satisfy the properties without changing the tree’s structure.
ii. Rotation – If recoloring is insufficient, rotation operations (left, right, left-right, right-left) are performed to restore the tree’s balance.
Q6- Which property ensures that no simple path from the root to a leaf is longer than twice as long as any other path in a red-black tree?
All paths from the root to the leaf nodes must have an equal number of black nodes.
The root node is always black.
Every red node must have black children.
A NIL (null) node is considered black.
Ans – (1)
Explanation – This property ensures that the red-black tree is always balanced, preventing excessively long paths from the root to any leaf node.
Q7- Which operation is used in a Red-Black Tree to change the pointer structure of the tree?
Recoloring
Left Rotation
Right Rotation
Deletion
Ans – (2 and 3)
Explanation – Left Rotation and Right Rotation are used in a Red-Black Tree to change the pointer structure of the tree during balancing.
Q8- When is recoloring applied in a Red-Black Tree?
After every insertion
After every deletion
When a red node has red children
When the root node is black
Ans – (3)
Explanation – Recoloring is applied in a Red-Black Tree when a red node has red children to restore the tree’s balance.
Q9- What is the time complexity of searching for a node in a Red-Black Tree with n nodes?
O(log n)
O(n)
O(1)
O(n*log n)
Ans – (1)
Explanation – The time complexity of searching for a node in a Red-Black Tree is O(log n) due to its self-balancing property, making it efficient for search operations.






