In the recurrence tree method, we make a tree with the help of the recurrence equation.
The recurrence tree method is a mathematical technique used to analyze the time complexity of recursive algorithms. It is commonly employed when solving recurrence relations that arise in divide-and-conquer algorithms.
The recurrence tree method becomes impractical when the tree becomes too large and complex. This occurs with algorithms that have a large number of recursive calls or when each recursive call creates multiple subproblems.
The main steps of recurrence tree method are
- Identify the recurrence relation for the algorithm.
- Draw the recurrence tree, showing recursive calls and their sizes.
- Calculate the work done at each level of the tree.
- Sum up the work done across all levels to obtain the time complexity.
The height of the recurrence tree corresponds to the number of times the problem is divided into smaller subproblems until reaching the base case. It is typically represented as log base b of n, where b is the factor by which the problem size reduces at each recursive call.
If the equation is T(n) = a T(n/b) + C, where a and b are constants, and C is c1*nk, where c1 and k are constants, then we make a recurrence tree.
Example 1 Draw the recurrence relation T(n) = 2T(n/2) + n
Compiling Time = 2T(n/2), Running Time = n
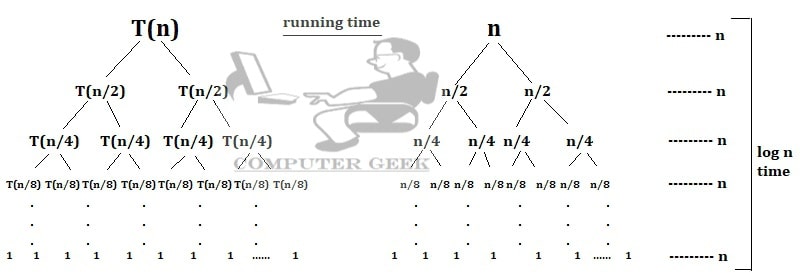
After summation all the operations = n + n + n + … + n [log n time]
= n.logn
= O(n.logn)
Example 2 Draw the recurrence relation T(n) = 2T(n/2) + n^2
Compiling Time = 2T(n/2), Running Time = n^2

After summation of all the operations
= n^2 + (n^2)/2 + (n^2)/4 + (n^2)/8 + …. + 1
= n^2 [ 1 + 1/2 + 1/4 + 1/8 + …. + 1/n^2]
This is a G.P. Series with r = 1/2
= n^2 [ 1 / (1 – 1/2) ]
= O(n^2) is the Ans.
Example 3 Draw the recurrence relation T(n) = T(n/3) + T(2n/3) + n
Compiling Time = T(n/3) + T(2n/3), Running Time = n
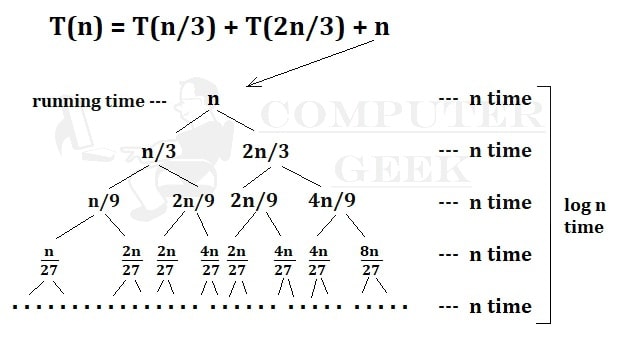
After summation all the operations = n + n + n + … + n [log n time]
= n.logn
= O(n.logn) is the Ans
Limitations of Recurrence Tree Method
The recurrence tree method assumes that each subproblem’s size is exactly the same at every recursive call, which may not hold for some algorithms. It also does not account for overhead from recursive calls and ignores non-recursive operations within the algorithm.
Advantages of Recurrence Tree Method
- Visualization– The recurrence tree method provides an intuitive visual representation of how the recursive algorithm breaks down the problem into subproblems and combines their results. This visualization aids in understanding the algorithm’s recursive structure and identifying patterns.
- Step-by-Step Analysis– The method follows a step-by-step approach, making it easier to track the recursive calls and their sizes. This organized analysis allows for a systematic examination of the algorithm’s time complexity.
- Suitable for Divide-and-Conquer Algorithms– The recurrence tree method is particularly effective for analyzing divide-and-conquer algorithms, where the problem is repeatedly divided into smaller subproblems.
Disadvantages of Recurrence Tree Method
- Limited Applicability– The recurrence tree method is not suitable for all types of recursive algorithms. It assumes that each subproblem is of equal size, which might not be true for algorithms with irregular recursive calls or varying problem sizes.
- Complexity– For algorithms with a large number of recursive calls or deep recursion levels, the recurrence tree can become extensive and challenging to draw and analyze manually. This complexity may lead to errors in the analysis.
- Ignores Overhead– The method focuses solely on the work done in recursive calls and ignores any overhead associated with the recursive process, such as the cost of function calls and memory allocation. This oversight can lead to an incomplete understanding of the algorithm’s time complexity.
- Difficulties with Non-Recursive Operations– If the algorithm involves significant non-recursive operations, the recurrence tree method might not accurately capture their impact on the overall time complexity, leading to an incomplete analysis.
Test Yourself
Q1- What is the recurrence tree method, and when is it used in algorithm analysis?
The recurrence tree method is a technique used to analyze the time complexity of recursive algorithms. It helps in solving recurrence relations that arise in divide-and-conquer algorithms, such as merge sort or quicksort.
Q2- How does the recurrence tree method work to analyze the time complexity of recursive algorithms?
The recurrence tree method breaks down the recursive algorithm into a tree-like structure, where each level represents a recursive call. The time complexity is then determined by summing up the costs at each level of the tree.
Q3- Can you apply the recurrence tree method to non-recursive algorithms?
The recurrence tree method is specifically designed for analyzing recursive algorithms. It may not be suitable for non-recursive algorithms as they follow a different flow of execution.
Q4- Are there any situations where the recurrence tree method is not the best approach for time complexity analysis?
The recurrence tree method may not be the best choice for analyzing algorithms with multiple nested recursive calls or varying subproblem sizes at different levels. In such cases, other techniques like the master theorem or substitution method may be more suitable.
Q5- Can the recurrence tree method be applied to analyze space complexity as well?
While the recurrence tree method is primarily used for time complexity analysis, a similar approach can be adapted to analyze the space complexity of recursive algorithms. In this case, the tree would represent the memory allocation at each recursive call.
Q6- When applying the recurrence tree method, what should be the focus in determining the time complexity if an algorithm is divided into two subproblems, one bigger and one smaller?
In a recurrence tree method, if T(n) is divided into two subproblems, one of which is bigger and the other smaller, the longer line in the recurrence tree will be associated with the bigger subproblem. The length of the longer line represents the dominant part of the algorithm’s time complexity.
The time complexity of the algorithm is determined by the longer line in the recurrence tree because the larger subproblem generally contributes more to the overall running time. The smaller subproblem might still be important for the overall complexity, but its impact becomes relatively less significant as the input size grows.
To calculate the time complexity using the recurrence tree method, you should consider the larger subproblem’s contribution to the overall time complexity. Simply taking the smaller line and neglecting the bigger subproblem would not provide an accurate representation of the algorithm’s time complexity.






