Recurrence Relation

Recurrence Relation

Definition: A recurrence relation calls itself. 

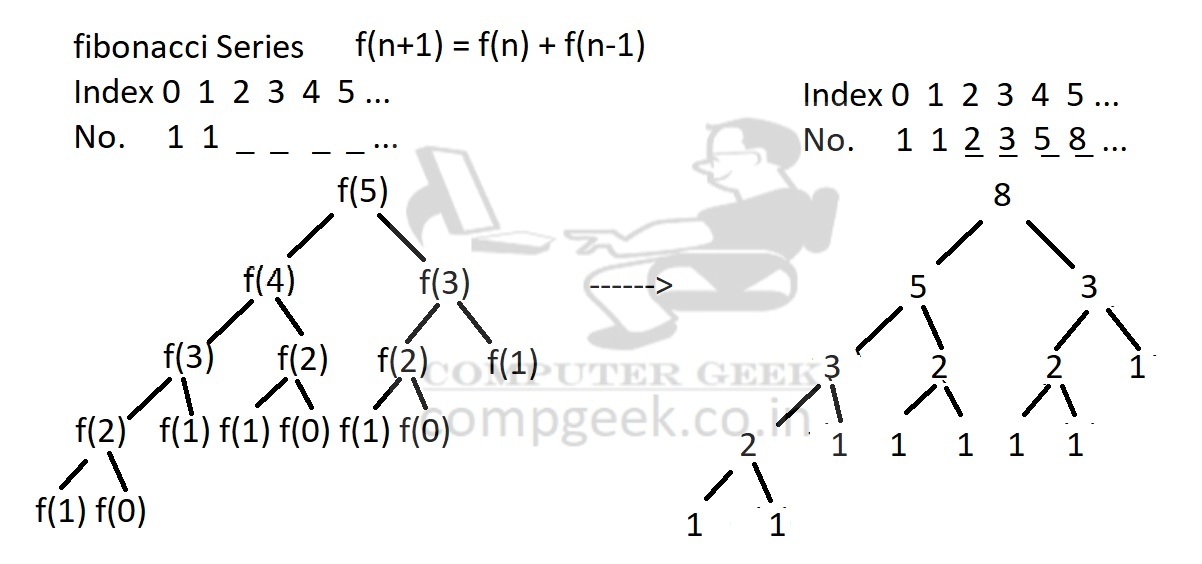
Example – Fibonacci series

1   1   2   3   5   8   13   21    34    55 . . . 

In this, sequence is made by the addition of the last two terms

1 + 1 = 2,   1 + 2 = 3,   2 + 3 = 5…

Recurrence function     f(n + 1) = f(n) + f(n – 1)

Recurrence –

It is a mathematical function to approximate the recursion function in the context of time complexity and the number of comparisons. 

Let T(n) is a mathematical function to approximate recursive function. 

Rules of recurrence – 

1. If the given instance of the problem is small or simple enough, just solve it.
2. Otherwise, reduce the problem to one or more, simpler instances of the same problem.

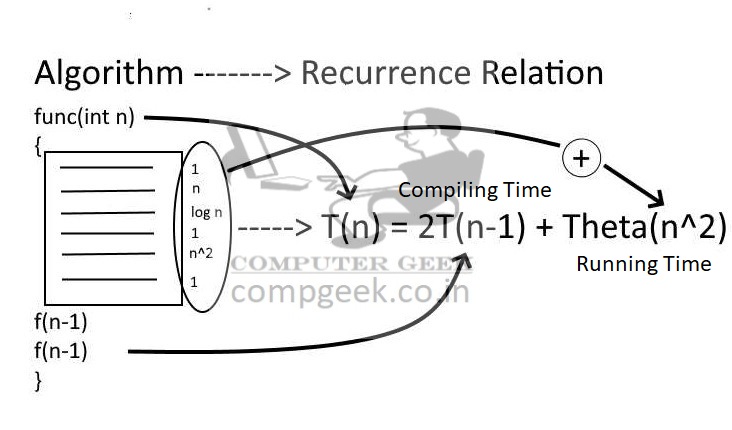
Algorithms of Recurrence Relation

Algorithm 1
f1(int n)

{

  if (n <= 1 )

      return;

  f1(n-1);

}

Recurrence function – 

T(1) = Θ(1)

T(n) = T(n – 1) + Θ(1)                    

T(n – 1) is compiling time and Θ(1)  is running time.

Trial – 

If n = 1, then T(1) = Θ(1)

If n = 2, then we find f(1)

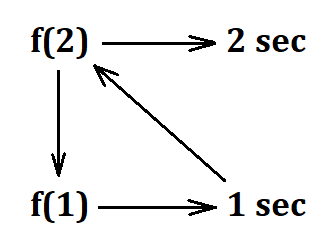
Algorithm 2

f2(int n)

{

  if (n <= 1)

     return;

  f2(n/2);

}

Recurrence function – 

T(1) = Θ(1)

T(n) = T(n/2) + Θ(1)                     

T(n/2) is compiling time and Θ(1)  is running time.