Introduction
.
The “Rat in a Maze” problem is a classic example used to explain the backtracking algorithm.
Imagine a rat placed at the top-left corner of a grid (or maze) that needs to find its way to the bottom-right corner. The grid contains open paths (cells where the rat can move) and blocked paths (cells where the rat cannot move).
The goal is to find a path from the starting point to the destination using backtracking.
The problem demonstrates how to systematically explore different possible paths and backtrack if a path leads to a dead end.
.
Historical Context
The “Rat in a Maze” problem is rooted in the general category of maze-solving algorithms, which have been studied for centuries. The problem became particularly prominent in the mid-20th century when computer science began exploring systematic problem-solving techniques.
The bhool bhulaiya in Indian culture can be seen as an early, real-world example of the challenges that the “Rat in a Maze” problem represents in computer science. Both involve navigating complex paths and finding a solution through exploration and sometimes backtracking, making the connection between them both interesting and educational.
The Bara Imambara in Lucknow, built by Nawab Asaf-ud-Daula in the 18th century, is famous for its bhool bhulaiya. The labyrinthine passages are designed to confuse and challenge those who enter, much like a maze in the “Rat in a Maze” problem.
.
Problem Statement
Given a 2D grid (maze), a rat is placed at the starting position (top-left corner) and needs to find a path to a piece of cheese located at the destination (bottom-right corner). The maze consists of open cells where the rat can move and blocked cells that the rat cannot pass through. The rat can only move in two directions: down and right.
The task is to determine a path from the starting point to the cheese.

If the rat is only allowed to move in two directions—down and right—and it moves down into a cell where both the right and further down directions are blocked, the rat will indeed be stuck.
In this scenario, because the rat is not allowed to move up or left, it cannot backtrack to try another path.
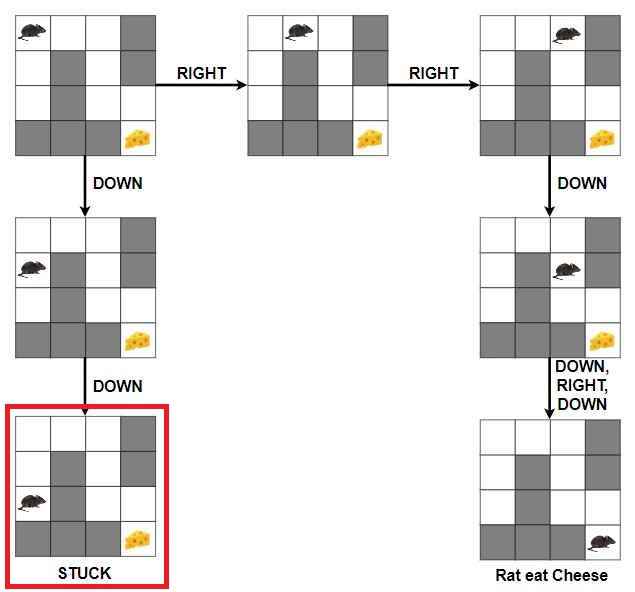
There are 50-50% chance that rat will go down or right.
If he goes to right cell, he will get the cheese and the algorithm will conclude that this path leads to a solution and gives the track in which the rat moves to get the cheese.
But if the rat will go down, then he will stuck into a cell where right and down directions are blocked, and only right and down directions he can move, the algorithm will conclude that this path does not lead to a solution. The rat cannot backtrack by moving up, so it gets stuck.
No Backtracking Possible – Since the rat cannot move up or left, there is no way for it to return to a previous position to try an alternative route.
Stuck Scenario – If the rat reaches a position where both the possible moves (down and right) are blocked, the algorithm will conclude that this path does not lead to a solution.
Result – The algorithm must then return “no solution” for that particular path, and if this was the only path attempted (given the constraints), the rat would be unable to reach the destination.
.
Rat in a Maze by Backtracking
If backtracking is allowed in the “Rat in a Maze” problem, the rat can explore different paths, even after encountering a dead end.
Backtracking with Down and Right Moves
In this scenario, the rat can initially move down or right, but if it reaches a dead end, it can backtrack (undo the last move) and try a different direction. This means the rat is not limited to continuing in one direction and can explore alternative paths.
- Backtracking – If the rat moves down and hits a dead end (where both right and further down are blocked), it can backtrack to the previous cell and try moving right instead.
- Exploration – The rat systematically explores all possible paths by moving in one direction, and if that path fails, it backtracks and tries the other direction.
- Finding the Cheese – Backtracking ensures that even if the initial path leads to a dead end, the rat can find a valid path by revisiting earlier cells and trying different routes.
.
Algorithm
- Start at the Top-Left Corner
- Place the rat at the starting position (0, 0).
- Check the Current Position
- If the current position is the cheese (i.e., (N-1, N-1)), print the path and stop.
- If the current position is out of bounds or blocked, backtrack (go back to the previous position).
- Mark the Current Position as Part of the Path.
- Try Moving Down
- Move to the cell (x + 1, y) (down).
- Recursively try to find the cheese from this new position.
- If Moving Down Doesn’t Work, Try Moving Right
- Move to the cell (x, y + 1) (right).
- Recursively try to find the cheese from this new position.
- If Both Down and Right move are Blocked, Backtrack
- Unmark the current cell as part of the path.
- Return to the previous cell to try another direction.
- Repeat the Process Until the Cheese is Found or All Possible Paths Have Been Tried.
.
Example –

Consider the same 4×4 maze. Now rat is in the top-left corner (0, 0) and move down.
![]()
.
Now, rat is in the position of (2, 0) means dead end where the rat cannot move right or down.
Here enters backtracking, where rat can backtrack and try a different direction. This means rat is not limited to continuing in one direction and can explore alternative paths.
![]()
.
The rat starts at cell (0, 0), take the alternative path, then moves to cell (0, 1), followed by cell (0, 2). Next, the rat moves to cell (1, 2), then to cell (2, 2), followed by cell (2, 3), and finally reaches the destination at cell (3, 3). Rat will eat the cheese and backtracking algorithm is successful.
![]()
.
Source Code for Rat in a Maze
// COMPUTER GEEK – compgeek.co.in
// Write a program for Rat in a Maze by Backtracking
#include <stdio.h>
#define N 100 // Maximum size of the maze
int maze[N][N], solution[N][N];
int n; // Size of the maze
// Function to print the solution matrix
void printSolution() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
printf(“%d “, solution[i][j]);
}
printf(“\n”);
}
}
// Function to check if the rat can move to maze[x][y]
int isSafe(int x, int y) {
return (x >= 0 && x < n && y >= 0 && y < n && maze[x][y] == 1);
}
// Function to solve the maze using backtracking
int solveMaze(int x, int y) {
// Base case: If the rat has reached the destination
if (x == n – 1 && y == n – 1) {
solution[x][y] = 1;
return 1;
}
// Check if the current move is safe
if (isSafe(x, y)) {
solution[x][y] = 1; // Mark this cell as part of the path
// Move right in the x direction
if (solveMaze(x, y + 1)) {
return 1;
}
// Move down in the y direction
if (solveMaze(x + 1, y)) {
return 1;
}
// If neither right nor down works, backtrack
solution[x][y] = 0;
return 0;
}
return 0;
}
int main() {
// Input the size of the maze
printf(“Enter the size of the maze: “);
scanf(“%d”, &n);
// Input the maze
printf(“Enter the maze matrix (%d x %d):\n”, n, n);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
scanf(“%d”, &maze[i][j]);
}
}
// Initialize the solution matrix to 0
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
solution[i][j] = 0;
}
}
// Solve the maze
if (solveMaze(0, 0)) {
printf(“Path found:\n”);
printSolution();
} else {
printf(“No path found\n”);
}
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Rat in a Maze by Backtracking
#include <iostream>
using namespace std;
#define N 100 // Maximum size of the maze
int maze[N][N], solution[N][N];
int n; // Size of the maze
// Function to print the solution matrix
void printSolution() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cout << solution[i][j] << ” “;
}
cout << endl;
}
}
// Function to check if the rat can move to maze[x][y]
bool isSafe(int x, int y) {
return (x >= 0 && x < n && y >= 0 && y < n && maze[x][y] == 1);
}
// Function to solve the maze using backtracking
bool solveMaze(int x, int y) {
// Base case: If the rat has reached the destination
if (x == n – 1 && y == n – 1) {
solution[x][y] = 1;
return true;
}
// Check if the current move is safe
if (isSafe(x, y)) {
solution[x][y] = 1; // Mark this cell as part of the path
// Move right in the x direction
if (solveMaze(x, y + 1))
return true;
// Move down in the y direction
if (solveMaze(x + 1, y))
return true;
// If neither right nor down works, backtrack
solution[x][y] = 0;
return false;
}
return false;
}
int main() {
// Input the size of the maze
cout << “Enter the size of the maze: “;
cin >> n;
// Input the maze
cout << “Enter the maze matrix (” << n << ” x ” << n << “):” << endl;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
cin >> maze[i][j];
// Initialize the solution matrix to 0
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
solution[i][j] = 0;
// Solve the maze
if (solveMaze(0, 0)) {
cout << “Path found:” << endl;
printSolution();
} else {
cout << “No path found” << endl;
}
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Rat in a Maze by Backtracking
import java.util.Scanner;
public class RatInMaze {
static int N; // Size of the maze
static int[][] maze, solution;
// Function to print the solution matrix
static void printSolution() {
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
System.out.print(solution[i][j] + ” “);
}
System.out.println();
}
}
// Function to check if the rat can move to maze[x][y]
static boolean isSafe(int x, int y) {
return (x >= 0 && x < N && y >= 0 && y < N && maze[x][y] == 1);
}
// Function to solve the maze using backtracking
static boolean solveMaze(int x, int y) {
// Base case: If the rat has reached the destination
if (x == N – 1 && y == N – 1) {
solution[x][y] = 1;
return true;
}
// Check if the current move is safe
if (isSafe(x, y)) {
solution[x][y] = 1; // Mark this cell as part of the path
// Move right in the x direction
if (solveMaze(x, y + 1))
return true;
// Move down in the y direction
if (solveMaze(x + 1, y))
return true;
// If neither right nor down works, backtrack
solution[x][y] = 0;
return false;
}
return false;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// Input the size of the maze
System.out.print(“Enter the size of the maze: “);
N = scanner.nextInt();
maze = new int[N][N];
solution = new int[N][N];
// Input the maze
System.out.println(“Enter the maze matrix (” + N + ” x ” + N + “):”);
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
maze[i][j] = scanner.nextInt();
// Initialize the solution matrix to 0
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
solution[i][j] = 0;
// Solve the maze
if (solveMaze(0, 0)) {
System.out.println(“Path found:”);
printSolution();
} else {
System.out.println(“No path found”);
}
scanner.close();
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for Rat in a Maze by Backtracking
def printSolution(solution, n):
for i in range(n):
for j in range(n):
print(solution[i][j], end=” “)
print()
def isSafe(maze, x, y, n):
return x >= 0 and x < n and y >= 0 and y < n and maze[x][y] == 1
def solveMaze(maze, x, y, solution, n):
# Base case: If the rat has reached the destination
if x == n – 1 and y == n – 1:
solution[x][y] = 1
return True
# Check if the current move is safe
if isSafe(maze, x, y, n):
solution[x][y] = 1 # Mark this cell as part of the path
# Move right in the x direction
if solveMaze(maze, x, y + 1, solution, n):
return True
# Move down in the y direction
if solveMaze(maze, x + 1, y, solution, n):
return True
# If neither right nor down works, backtrack
solution[x][y] = 0
return False
return False
def main():
# Input the size of the maze
n = int(input(“Enter the size of the maze: “))
# Input the maze
print(f”Enter the maze matrix ({n} x {n}):”)
maze = []
for _ in range(n):
maze.append(list(map(int, input().split())))
# Initialize the solution matrix to 0
solution = [[0 for _ in range(n)] for _ in range(n)]
# Solve the maze
if solveMaze(maze, 0, 0, solution, n):
print(“Path found:”)
printSolution(solution, n)
else:
print(“No path found”)
if __name__ == “__main__”:
main()
Enter the size of the maze: 4
Enter the maze matrix (4 x 4):
1 1 1 0
1 0 1 0
1 0 1 1
0 0 0 1
Path found:
1 1 1 0
0 0 1 0
0 0 1 1
0 0 0 1
=== Code Execution Successful ===
Time Complexity
If there are N x N cells in the maze, and the rat can potentially move in two directions at each cell, the number of possible paths the algorithm might explore is O(2(N*N)).
However, due to constraints (blocked cells or boundaries), not all paths will be valid, but the time complexity remains exponential in the worst case.
There can be 2(N^2) possible paths to check in the worst case.
.
Space Complexity
The space complexity of the “Rat in a Maze” problem using backtracking depends primarily on two factors, the auxiliary space required for the recursion stack and the space needed for the solution matrix.
If the maze size is N x N, then the space required for the solution matrix is O(N2).
The maximum depth of the recursion stack is proportional to the size of the maze. In the worst case, the recursion can go as deep as N + N – 1. It means at most O(N) space is required.
Thus, the overall space complexity is O(N2) + O(N) = O(N2).
.
Applications
- In robotics, pathfinding algorithms help a robot navigate through a grid or a maze-like environment. The “Rat in a Maze” algorithm is a fundamental example that can be expanded to develop more complex robotic pathfinding algorithms.
- Many video games use maze-like structures where the goal is to find a path from a start point to an end point. The backtracking approach helps in generating and solving these mazes.
- In computer networks, finding the shortest or optimal path for data packets from the source to the destination can be seen as a maze problem. Though more advanced algorithms like Dijkstra’s or A* are used, the backtracking approach forms the basis for understanding routing in networks.
- In designing circuit boards, backtracking can help find paths for connecting different components on a PCB (Printed Circuit Board) without causing a short circuit.
- Backtracking algorithms are used in pattern matching problems where the goal is to find a specific pattern in a large dataset or grid.
- In data mining, exploring all possible paths to find optimal solutions or patterns within a dataset can be modelled using backtracking techniques.
- The process of predicting protein structures from amino acid sequences often involves exploring many possible configurations, similar to exploring paths in a maze.
Test Yourself
Q1- Explain the concept of backtracking in the context of the “Rat in a Maze” problem.
Backtracking involves exploring a path, and if it leads to a dead end or invalid state, the algorithm retraces its steps to the previous decision point and tries a different path.
In the “Rat in a Maze” problem, if the rat encounters a dead end, it backtracks to previous cells to explore other directions (down or right) until it either finds the cheese or determines no solution exists.
Q2- What are the limitations of the “Rat in a Maze” problem when the rat can only move down and right and no backtracking is there?
When the rat can only move down and right, it may face scenarios where it cannot backtrack if it encounters a dead end.
This restriction limits the exploration of alternative paths and can lead to situations where the rat gets stuck if no valid paths are available without the ability to move up or left.
Q3- Discuss how the “Rat in a Maze” problem can be adapted for a robot navigation system.
In a robot navigation system, the “Rat in a Maze” problem can be adapted to help the robot find its way through a maze-like environment.
The robot would use similar backtracking algorithms to explore paths, avoid obstacles, and reach its destination, adjusting the moves to accommodate real-world constraints and more complex navigation requirements.
Q4- How can the “Rat in a Maze” problem be modified to allow movement in all four directions (up, down, left, right)?
To modify the “Rat in a Maze” problem for movement in all four directions, the algorithm must be adjusted to include checks for all possible moves.
This involves expanding the recursive function to explore up and left directions as well, handling additional edge cases, and ensuring that the maze-solving logic accommodates all four movement directions.
Q5- What is the primary goal of the “Rat in a Maze” problem?
To find the shortest path in a maze
To determine if a path exists from start to finish
To solve a puzzle with multiple solutions
To explore all possible paths in the maze
Ans – (2)
Explanation – The primary goal is to find if there is a viable path from the start to the destination, rather than finding the shortest path or solving a multi-solution puzzle.
Q6- In the “Rat in a Maze” problem, what does the backtracking algorithm do when encounter a dead end?
Moves to a different maze
Repeats the same path
Retraces its steps to try a different path
Ends the search
Ans – (3)
Explanation – The algorithm backtracks to previous decision points to explore alternative paths when a dead end is reached.
Q7- What is the time complexity of the “Rat in a Maze” problem in the worst case?
O(N)
O(N^2)
O(2^(N*N))
O(N log N)
Ans – (3)
Explanation – The time complexity is exponential due to the potential number of paths explored, which can be as high as 2^(N*N) in the worst case.
Q8- Which of the following is a limitation of the backtracking algorithm for the “Rat in a Maze” problem?
It always finds the shortest path
It cannot handle dynamic mazes
It has exponential time complexity
It is not suitable for small mazes
Ans – (3)
Explanation – The backtracking algorithm can be slow for large mazes due to its exponential time complexity, although it is not limited by the maze size itself.
Q9- What does the “isSafe” function check in the context of the “Rat in a Maze” problem?
If the maze is solvable
If the current cell is within bounds and not blocked
If the destination is reached
If the rat has moved correctly
Ans – (2)
Explanation – The “isSafe” function ensures that the rat is moving to a valid and accessible cell in the maze.
Q10- In which application is the “Rat in a Maze” algorithm NOT typically used?
Game level design
Network routing
DNA sequencing
Image compression
Ans – (4)
Explanation – The “Rat in a Maze” algorithm is not used for image compression, but it is applicable in game design, network routing, and DNA sequencing.
Q11- How does the space complexity of the “Rat in a Maze” problem relate to recursion?
It depends on the number of recursive calls
It is unaffected by recursion
It is lower for large mazes
It depends on the maze size but not recursion
Ans – (1)
Explanation – The space complexity includes the recursion stack, which grows with the depth of recursive calls.






