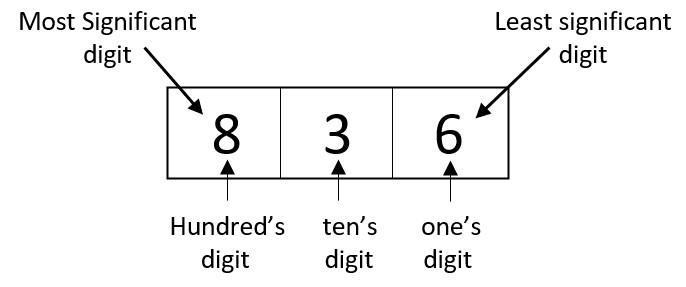
Radix (Root or Base number) is the number of unique digits, used to represent numbers in a positional numerical system.
.
History
As early as 1923, punched card sorting was done widely using radix sorting algorithms. Harold H. Seward created this sorting method’s first memory-efficient computer algorithm at MIT in 1954.
.
Example –
In binary, the radix, or base number, is equal to 2.
In octal, the radix, or base number, is equal to 8.
In decimal, the radix, or base number, is equal to 10.
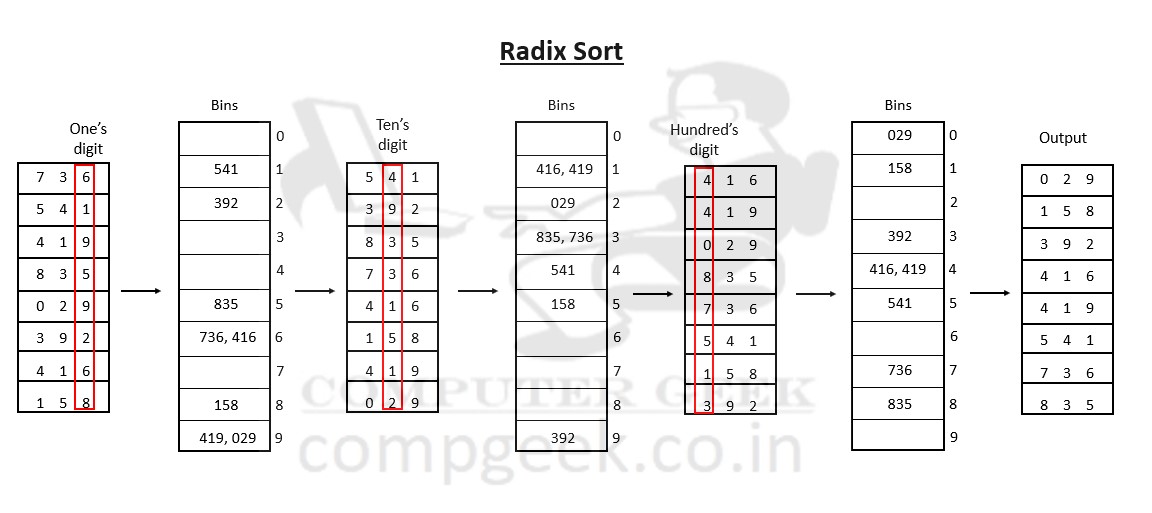
- It is a non-comparison sort. It eliminates comparison by creating bins and dividing elements into bins based on their radix.
- Each digit is sorted from least significant digit to most significant digit.
- Radix sort will sort the digits in the one’s place, then the ten’s place, then the hundred’s place and so on.
- We have to find the maximum element in the input array. Let’s say the maximum element is 836. So, we sort 3 times to arrange all the elements into its correct positions.
Working
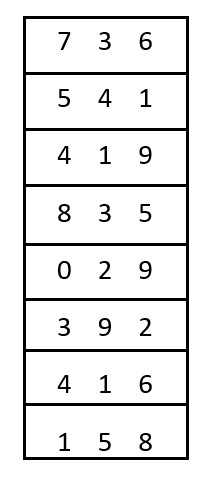
We have an input where n = 8.
Input = {736, 541, 419, 835, 29, 392, 416, 158}
Maximum number = 835
Number of digits in maximum number = 3
We have to sort 3 times to get the sorted output. Also, 29 has only 2 digits, so we will add a zero (029) as the most significant digit.
Take the least significant one’s digit and sort it, after that sort ten’s digit and lastly hundred’s digit. The diagram below represents the workings of radix sort.
- Enter the input array.
- Take the maximum element in the array and count digits.
- for sort <– 1 to digit Sort the array with significant digit with an in-place sort
Program of Radix Sort in C
// Write a program for Radix Sort
// COMPUTER GEEK – compgeek.co.in
// Write a program for Radix Sort
#include <iostream>
using namespace std;
void radix(int array[], int n, int max);
int main() {
int array[100], size, i, max = 0;
// Input array declaration
cout << “Enter the size of the array: “;
cin >> size;
// Input array initialization
cout << “Enter the ” << size << ” items of the array: “;
for (i = 0; i < size; i++) {
cin >> array[i];
if (array[i] > max) {
max = array[i];
}
}
radix(array, size, max);
// Array after Radix array
cout << “\nThe Sorted array is: “;
for (i = 0; i < size; i++) {
cout << array[i] << ” “;
}
return 0;
}
void radix(int array[], int n, int max) {
int bins[10][10], count[10];
int i, j, k, rem, divisor = 1, sort, digit = 0;
while (max > 0) {
digit++;
max = max / 10;
}
// We have to sort digit times
for (sort = 1; sort <= digit; sort++) {
// Reset count array
for (i = 0; i < 10; i++) {
count[i] = 0;
}
for (i = 0; i < n; i++) {
// remainder of 321 % 10 is 1.
rem = (array[i] / divisor) % 10;
bins[rem][count[rem]] = array[i];
count[rem] += 1;
}
divisor = divisor * 10;
i = 0;
for (k = 0; k < 10; k++) {
for (j = 0; j < count[k]; j++) {
array[i] = bins[k][j];
i++;
}
}
}
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Radix Sort
import java.util.Scanner;
public class RadixSort {
public static void radix(int[] array, int n, int max) {
int[][] bins = new int[10][10];
int[] count = new int[10];
int i, j, k, rem, divisor = 1, sort, digit = 0;
while (max > 0) {
digit++;
max = max / 10;
}
// We have to sort digit times
for (sort = 1; sort <= digit; sort++) {
// Reset count array
for (i = 0; i < 10; i++) {
count[i] = 0;
}
for (i = 0; i < n; i++) {
// remainder of 321 % 10 is 1.
rem = (array[i] / divisor) % 10;
bins[rem][count[rem]] = array[i];
count[rem] += 1;
}
divisor = divisor * 10;
i = 0;
for (k = 0; k < 10; k++) {
for (j = 0; j < count[k]; j++) {
array[i] = bins[k][j];
i++;
}
}
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int[] array = new int[100];
int size, i, max = 0;
// Input array declaration
System.out.print(“Enter the size of the array: “);
size = scanner.nextInt();
// Input array initialization
System.out.print(“Enter the ” + size + ” items of the array: “);
for (i = 0; i < size; i++) {
array[i] = scanner.nextInt();
if (array[i] > max) {
max = array[i];
}
}
radix(array, size, max);
// Array after Radix array
System.out.print(“\nThe Sorted array is: “);
for (i = 0; i < size; i++) {
System.out.print(array[i] + ” “);
}
scanner.close();
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for Radix Sort
def radix(array, n, max_val):
bins = [[] for _ in range(10)]
count = [0] * 10
divisor = 1
digit = 0
while max_val > 0:
digit += 1
max_val //= 10
for sort in range(1, digit + 1):
for i in range(10):
count[i] = 0
for i in range(n):
rem = (array[i] // divisor) % 10
bins[rem].append(array[i])
count[rem] += 1
divisor *= 10
i = 0
for k in range(10):
for j in range(count[k]):
array[i] = bins[k][j]
i += 1
def main():
array = [0] * 100
size = int(input(“Enter the size of the array: “))
max_val = 0
print(“Enter the”, size, “items of the array: “)
for i in range(size):
array[i] = int(input())
if array[i] > max_val:
max_val = array[i]
radix(array, size, max_val)
print(“\nThe Sorted array is: “, end=””)
for i in range(size):
print(array[i], end=” “)
if __name__ == “__main__”:
main()
Time & Space Complexity of Radix sort
- The average-case time complexity is O((n+b)*d). where n is number of inputs, b is radix or base number, because radix will create a new array equal to b. Also, d is the number of digits that maximum element has time complexity is (n+b)*d
- If ‘d’ digits are equal to n, then in worst-case time complexity is n2.
- If ‘d’ digits are equal to 1, then in best-case time complexity is n.
- The space complexity is O(n+b) where n is the number of inputs and b is the radix or base number.
Advantage of radix sort
- Radix sort is stable sort.
- Time complexity is linear.
Disadvantage of radix sort
- less flexible because it depends on digits or letters.
- The constants in the time complexity is greater than other algorithms.
- This sort is not in-place sort as it needs more space than other algorithms.
Test Yourself
Q1- Explain the concept of radix in radix sort and how it influences the sorting process.
Radix refers to the base number used in a positional numerical system. In radix sort, the elements are sorted based on their digits, with each digit representing a particular radix position. The sorting process starts from the least significant digit to the most significant digit. The radix value determines the number of unique digits possible in the input, and it affects the number of bins created during sorting. A higher radix can lead to a more efficient sorting process as it reduces the number of iterations required to sort the elements.
Q2- What is the time complexity of radix sort in the average case? Provide a brief explanation.
The average-case time complexity of radix sort is O((n+b)*d), where n is the number of inputs, b is the radix or base number, and d is the number of digits in the maximum element. The time complexity is derived from the number of iterations required to sort the elements based on each digit. Since radix sort processes the digits from least significant to most significant, the maximum number of iterations is equal to the number of digits in the largest element.
Q3- Explain why radix sort is considered a non-comparison sort and how it avoids comparison operations.
Radix sort is a non-comparison sort because it doesn’t rely on comparing elements to determine their relative order. Instead, it sorts elements based on their individual digits, starting from the least significant digit to the most significant digit. By dividing elements into bins based on their radix positions, it eliminates the need for comparison operations between elements during the sorting process. This approach results in a more efficient sorting algorithm.
Q4- What are the advantages of radix sort compared to other sorting algorithms?
- Radix sort preserves the relative order of equal elements, making it a stable sort.
- Its time complexity is linear, which can be favourable for large datasets.
- It doesn’t rely on comparisons, it can outperform comparison-based sorting algorithms in certain cases.
Q5- Discuss the space complexity of radix sort and explain why it is not an in-place sorting algorithm.
The space complexity of radix sort is O(n+b), where n is the number of inputs and b is the radix or base number.
Radix sort requires additional space to create bins for sorting elements based on their digits. As the radix value increases, the number of bins also increases, leading to higher space requirements. This additional space usage makes radix sort a non-in-place sorting algorithm, as it needs memory outside the original array to store the bins during sorting.
Q6- Can radix sort handle negative numbers? If yes, explain how it deals with negative integers during the sorting process.
Yes, radix sort can handle negative numbers.
During the sorting process, radix sort treats negative numbers by considering their sign as a part of their most significant digit. It ensures that negative numbers with the same absolute value are sorted in their appropriate positions relative to positive numbers.
The sorting algorithm sorts negative numbers with the most significant digit first, followed by the rest of the digits just like it does for positive numbers.
Q7- Compare the best-case and worst-case time complexity of radix sort. Under what circumstances would radix sort perform at its worst?
The best-case time complexity of radix sort is O(n) when the number of digits in the maximum element (d) is equal to 1.
In this scenario, the sorting process completes in a single pass as there is no need for further iterations.
The worst-case time complexity is O(n^2) when the number of digits (d) is equal to the number of inputs (n). This situation arises when all elements have the same number of digits, leading to the need for d iterations for n elements, resulting in the worst-case performance.
Q8- Discuss the main disadvantages of radix sort and situations where other sorting algorithms might be more suitable.
The main disadvantages of radix sort are its dependence on the number of digits or letters in the input and the larger constants in its time complexity compared to other sorting algorithms.
Radix sort may not be the best choice for datasets with variable-length elements or when the maximum element has a significantly larger number of digits than the rest of the elements. In such cases, algorithms like quicksort or mergesort, which have better average-case time complexity and are more flexible in handling various data types, might be more suitable.
Q9- What is the radix or base number in radix sort?
Number of elements in the input array
Number of unique digits in the input array
Number of comparisons required during sorting
Number of iterations to sort the array
Ans – (2)
Explanation – The radix or base number represents the number of unique digits used to represent numbers in the positional numerical system.
if the number of digits is 0, 1, 2, …, 9 then radix or base number is 10.
Q10- Radix sort is a non-comparison sort because:
It uses comparison operations efficiently
It doesn’t rely on comparing elements during sorting
It compares each element with all other elements
It compares elements based on their index positions
Ans – (2)
Explanation – Radix sort eliminates the need for comparison operations by dividing elements into bins based on their radix positions for sorting.
Q11- Which digit is sorted first in radix sort?
Least significant digit
Most significant digit
The digit with the highest value
The digit with the lowest value
Ans – (1)
Explanation – Radix sort starts sorting from the least significant digit and progresses to the most significant digit.
Q12- What is the space complexity of radix sort?
O(log n)
O(n)
O(n+b)
O(n^2)
Ans – (3)
Explanation – The space complexity of radix sort is O(n+b), where n is the number of inputs and b is the radix or base number.
Q13- When does radix sort perform at its worst?
When all elements have a single digit
When all elements have the same value
When the number of digits in the maximum element is equal to the number of inputs
When the radix value is small
Ans – (3)
Explanation – The worst-case time complexity of radix sort occurs when the number of digits in the maximum element is equal to the number of inputs, resulting in O(n^2) complexity.
Q14- Which sorting algorithms might be more suitable for datasets with variable-length elements?
Radix sort
Quicksort
Merge-sort
Insertion sort
Ans – (1)
Explanation – Merge-sort is suitable for datasets with variable-length elements as it can efficiently handle different sizes of elements during the sorting process. Radix sort is less flexible in this regard as it depends on the number of digits or letters in the input.






