Understanding Prim’s Algorithm
The algorithm was developed by Czech mathematician Vojtín Czernik in 1930 and later by computer scientists Robert C. Prim in 1957 and Edgard W. Dijkstra in 1959. Therefore, it is sometimes also called the Járnik algorithm, prim-Járnik algorithm, prime. -Dijkstra algorithm or DJP algorithm.
.
What is Prim’s Minimum Spanning Tree Algorithm?
Prim’s Algorithm is a greedy algorithm used for finding the minimum spanning tree (MST) of a connected, undirected graph.
- The goal of Prim’s algorithm is to connect all the vertices of the graph while minimizing the total weight of the edges in the spanning tree.
- The algorithm starts with an arbitrary vertex and grows the spanning tree by adding the shortest edge that connects a vertex in the tree to a vertex outside the tree at each step.
- The process continues until all vertices are included in the minimum spanning tree.
- Prim’s algorithm ensures that the resulting tree is acyclic and spans all the vertices with the least possible total edge weight.
.
Algorithm
- Begin with an arbitrary node.
- Find the shortest edge connecting any unvisited node to the current tree.
- Add the selected edge and the connected node to the tree.
- Repeat steps 2-3 until all nodes are included in the tree.
.
Working of Prim’s Algorithm
Imagine you have a network of houses, and you want to build roads between them with the least total distance.
Prim’s algorithm starts with a single node and adds the shortest edge that connects a new node to the existing structure at each step. It continues this process until all nodes are connected.

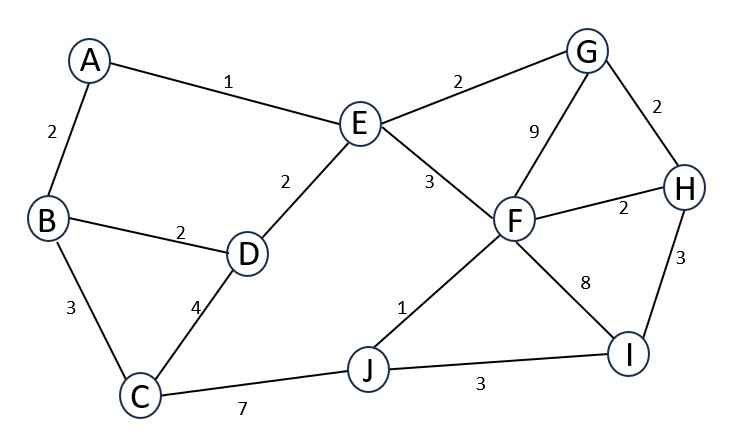
Let’s solve for the minimum spanning tree using Prim’s algorithm with the given graph –
Vertices: A, B, C, D, E, F, G, H, I, J
Edges with weights – 16
.
Initialization
Start with an arbitrary vertex, let’s say A.
Initialize an empty set T (the minimum spanning tree) and a priority queue or min-heap to store edges.
.
Adding Edges
Add the minimum-weight edge connected to A, which is AE (weight = 1). Update T.
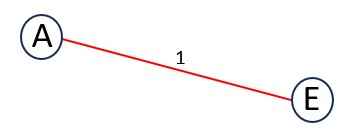
Now, add the next minimum-weight edge connected to A or E. So, the edges are {AB = 2, ED = 2, EG = 2, EF = 3}.
You have to select an edge of minimum weight which has one unvisited vertex, no cycles or loops in tree.
So, we select AB. Update T.

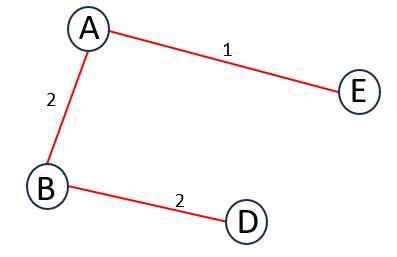
Now, add the next minimum-weight edge connected to A, B or E. So, the edges are {BD = 2, BC = 3, ED = 2, EG = 2, EF = 3}.
You have to select an edge of minimum weight which has one unvisited vertex, no cycles or loops in tree.
So, we select BD. Update T.
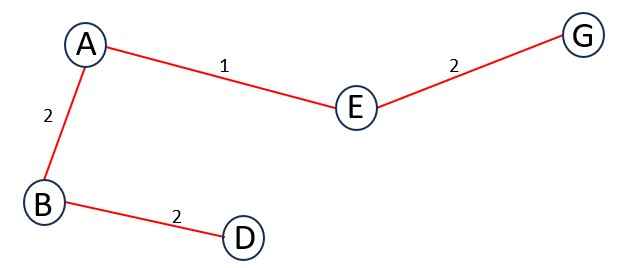
Now, add the next minimum-weight edge connected to A, B, D or E. So, the edges are {BC = 3, DC = 4, EG = 2, EF = 3}.
ED is not in the list because a cycle is formed.
You have to select an edge of minimum weight which has one unvisited vertex, no cycles or loops in tree.
So, we select EG. Update T.
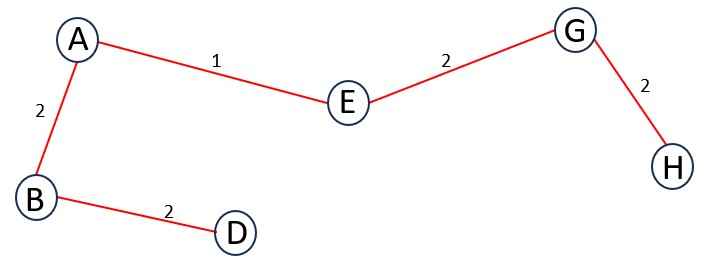
Now, add the next minimum-weight edge connected to A, B, D, E or G. So, the edges are {BC = 3, DC = 4, EF = 3, GF = 9, GH = 2}.
You have to select an edge of minimum weight which has one unvisited vertex, no cycles or loops in tree.
So, we select GH. Update T.
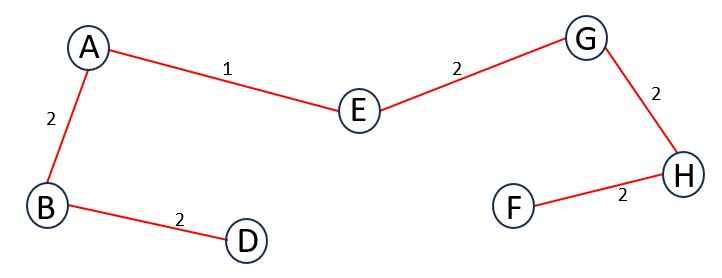
Now, add the next minimum-weight edge connected to A, B, D, E, G or H. So, the edges are {BC = 3, DC = 4, EF = 3, GF = 9, HF = 2, HI = 3}.
You have to select an edge of minimum weight which has one unvisited vertex, no cycles or loops in tree.
So, we select HF. Update T.
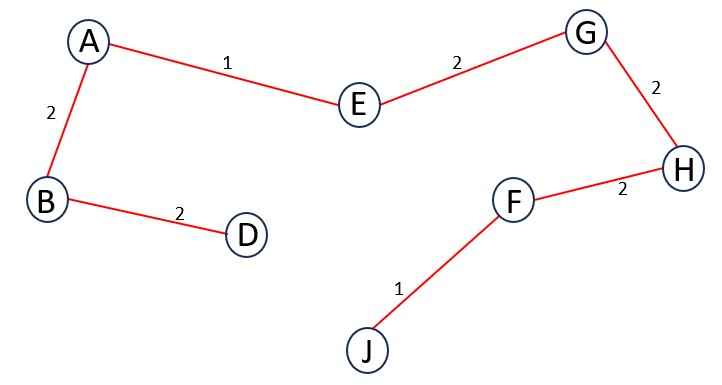
Now, add the next minimum-weight edge connected to A, B, D, E, G, H or F. So, the edges are {BC = 3, DC = 4, HI = 3, FJ = 1}.
EF and GF are not in the list because a cycle is formed.
You have to select an edge of minimum weight which has one unvisited vertex, no cycles or loops in tree.
So, we select FJ. Update T.
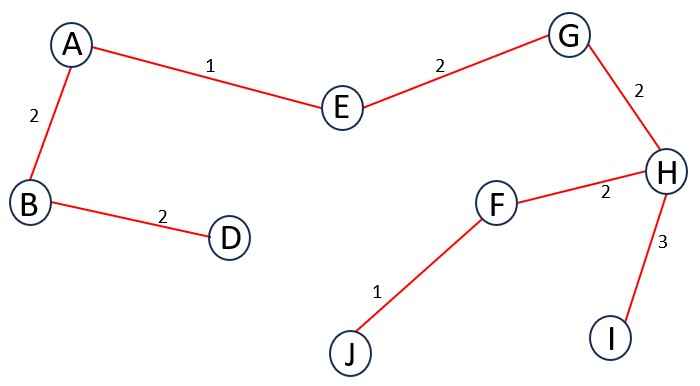
Now, add the next minimum-weight edge connected to A, B, D, E, G, H, F or J. So, the edges are {BC = 3, DC = 4, CJ = 7, HI = 3, FI = 8, JI = 3}.
You have to select an edge of minimum weight which has one unvisited vertex, no cycles or loops in tree.
So, we select HI. Update T.
Now, add the next minimum-weight edge connected to A, B, D, E, G, H, F, J or I. So, the edges are {BC = 3, DC = 4, CJ = 7}.
FI and JI are not in the list because a cycle is formed and there is no unvisited vertex.
You have to select an edge of minimum weight which has one unvisited vertex, no cycles or loops in tree.
So, we select BC. Update T.

The final minimum spanning tree.
The total weight of the minimum spanning tree is the sum of the weights of its edges.
Total Weight – 18
We can make multiple minimum spanning trees of prim’s with this graph and the total weight of their edges would be just 18 not more than that.
.
Source Code for Prim’s Algorithm
// COMPUTER GEEK – compgeek.co.in
// Write a program for Prim’s Algorithm
#include <stdio.h>
#include <limits.h>
// Number of vertices in the graph
#define V 5
// A utility function to find the vertex with minimum key value, from
// the set of vertices not yet included in MST
int minKey(int key[], int mstSet[])
{
// Initialize min value
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (mstSet[v] == 0 && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
// A utility function to print the constructed MST stored in parent[]
void printMST(int parent[], int n, int graph[V][V])
{
printf(“Edge Weight\n”);
for (int i = 1; i < V; i++)
printf(“%d – %d %d \n”, parent[i], i, graph[i][parent[i]]);
}
// Function to construct and print MST for a graph represented using adjacency
// matrix representation
void primMST(int graph[V][V])
{
int parent[V]; // Array to store constructed MST
int key[V]; // Key values used to pick the minimum weight edge in cut
int mstSet[V]; // To represent the set of vertices not yet included in MST
// Initialize all keys as INFINITE
for (int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = 0;
// Always include the first vertex in MST.
key[0] = 0; // Make key 0 so that this vertex is picked as the first vertex
parent[0] = -1; // First node is always the root of MST
// The MST will have V vertices
for (int count = 0; count < V – 1; count++)
{
// Pick the minimum key vertex from the set of vertices
// not yet included in MST
int u = minKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = 1;
// Update key value and parent index of the adjacent vertices of
// the picked vertex. Consider only those vertices which are not yet
// included in MST
for (int v = 0; v < V; v++)
// graph[u][v] is non-zero only for adjacent vertices of m
// mstSet[v] is false for vertices not yet included in MST
// Update the key only if graph[u][v] is smaller than key[v]
if (graph[u][v] && mstSet[v] == 0 && graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
// Print the constructed MST
printMST(parent, V, graph);
}
// Driver program to test the function
int main()
{
int graph[V][V];
// User input for the graph
printf(“Enter the adjacency matrix for the graph with %d vertices:\n”, V);
for (int i = 0; i < V; i++)
for (int j = 0; j < V; j++)
scanf(“%d”, &graph[i][j]);
// Print the solution
primMST(graph);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Prim’s Algorithm
#include <iostream>
#include <climits>
using namespace std;
// Number of vertices in the graph
#define V 5
// A utility function to find the vertex with minimum key value, from
// the set of vertices not yet included in MST
int minKey(int key[], bool mstSet[])
{
// Initialize min value
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
// A utility function to print the constructed MST stored in parent[]
int printMST(int parent[], int n, int graph[V][V])
{
cout << “Edge Weight\n”;
for (int i = 1; i < V; i++)
printf(“%d – %d %d \n”, parent[i], i, graph[i][parent[i]]);
return 0;
}
// Function to construct and print MST for a graph represented using adjacency
// matrix representation
void primMST(int graph[V][V])
{
int parent[V]; // Array to store constructed MST
int key[V]; // Key values used to pick the minimum weight edge in cut
bool mstSet[V]; // To represent the set of vertices not yet included in MST
// Initialize all keys as INFINITE
for (int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = false;
// Always include the first vertex in MST.
key[0] = 0; // Make key 0 so that this vertex is picked as the first vertex
parent[0] = -1; // First node is always the root of MST
// The MST will have V vertices
for (int count = 0; count < V – 1; count++)
{
// Pick the minimum key vertex from the set of vertices
// not yet included in MST
int u = minKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = true;
// Update key value and parent index of the adjacent vertices of
// the picked vertex. Consider only those vertices
// which are not yet included in MST
for (int v = 0; v < V; v++)
// graph[u][v] is non-zero only for adjacent vertices of m
// mstSet[v] is false for vertices not yet included in MST
// Update the key only if graph[u][v] is smaller than key[v]
if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
// Print the constructed MST
printMST(parent, V, graph);
}
// Driver program to test the function
int main()
{
int graph[V][V];
// User input for the graph
cout << “Enter the adjacency matrix for the graph with ” << V << ” vertices:\n”;
for (int i = 0; i < V; i++)
for (int j = 0; j < V; j++)
cin >> graph[i][j];
// Print the solution
primMST(graph);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Prim’s Algorithm
import java.util.Scanner;
public class PrimMST {
// Number of vertices in the graph
private static final int V = 5;
// A utility function to find the vertex with minimum key value, from
// the set of vertices not yet included in MST
private static int minKey(int key[], boolean mstSet[]) {
// Initialize min value
int min = Integer.MAX_VALUE, min_index = -1;
for (int v = 0; v < V; v++)
if (!mstSet[v] && key[v] < min)
min = key[v];
for (int v = 0; v < V; v++)
if (!mstSet[v] && key[v] == min)
min_index = v;
return min_index;
}
// A utility function to print the constructed MST stored in parent[]
private static void printMST(int parent[], int n, int graph[][]) {
System.out.println(“Edge Weight”);
for (int i = 1; i < V; i++)
System.out.println(parent[i] + ” – ” + i + ” ” + graph[i][parent[i]]);
}
// Function to construct and print MST for a graph represented using adjacency
// matrix representation
private static void primMST(int graph[][]) {
int parent[] = new int[V]; // Array to store constructed MST
int key[] = new int[V]; // Key values used to pick the minimum weight edge in cut
boolean mstSet[] = new boolean[V]; // To represent the set of vertices not yet included in MST
// Initialize all keys as INFINITE
for (int i = 0; i < V; i++) {
key[i] = Integer.MAX_VALUE;
mstSet[i] = false;
}
// Always include the first vertex in MST.
key[0] = 0; // Make key 0 so that this vertex is picked as the first vertex
parent[0] = -1; // First node is always the root of MST
// The MST will have V vertices
for (int count = 0; count < V – 1; count++) {
// Pick the minimum key vertex from the set of vertices
// not yet included in MST
int u = minKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = true;
// Update key value and parent index of the adjacent vertices of
// the picked vertex. Consider only those vertices which are not yet
// included in MST
for (int v = 0; v < V; v++)
// graph[u][v] is non-zero only for adjacent vertices of m
// mstSet[v] is false for vertices not yet included in MST
// Update the key only if graph[u][v] is smaller than key[v]
if (graph[u][v] != 0 && !mstSet[v] && graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}
}
// Print the constructed MST
printMST(parent, V, graph);
}
// Driver program to test the function
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int graph[][] = new int[V][V];
// User input for the graph
System.out.println(“Enter the adjacency matrix for the graph with ” + V + ” vertices:”);
for (int i = 0; i < V; i++)
for (int j = 0; j < V; j++)
graph[i][j] = scanner.nextInt();
// Print the solution
primMST(graph);
scanner.close();
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for Prim’s Algorithm
# Number of vertices in the graph
V = 5
# A utility function to find the vertex with minimum key value, from
# the set of vertices not yet included in MST
def min_key(key, mst_set):
min_val = float(‘inf’)
min_index = -1
for v in range(V):
if not mst_set[v] and key[v] < min_val:
min_val = key[v]
min_index = v
return min_index
# A utility function to print the constructed MST stored in parent[]
def print_mst(parent, graph):
print(“Edge Weight”)
for i in range(1, V):
print(f”{parent[i]} – {i} {graph[i][parent[i]]}”)
# Function to construct and print MST for a graph represented using adjacency
# matrix representation
def prim_mst(graph):
parent = [-1] * V # Array to store constructed MST
key = [float(‘inf’)] * V # Key values used to pick the minimum weight edge in cut
mst_set = [False] * V # To represent the set of vertices not yet included in MST
# Always include the first vertex in MST.
key[0] = 0 # Make key 0 so that this vertex is picked as the first vertex
parent[0] = -1 # First node is always the root of MST
# The MST will have V vertices
for count in range(V – 1):
# Pick the minimum key vertex from the set of vertices
# not yet included in MST
u = min_key(key, mst_set)
# Add the picked vertex to the MST Set
mst_set[u] = True
# Update key value and parent index of the adjacent vertices of
# the picked vertex. Consider only those vertices which are not yet
# included in MST
for v in range(V):
# graph[u][v] is non-zero only for adjacent vertices of m
# mst_set[v] is False for vertices not yet included in MST
# Update the key only if graph[u][v] is smaller than key[v]
if graph[u][v] != 0 and not mst_set[v] and graph[u][v] < key[v]:
parent[v] = u
key[v] = graph[u][v]
# Print the constructed MST
print_mst(parent, graph)
# Driver program to test the function
if __name__ == “__main__”:
graph = []
# User input for the graph
print(f”Enter the adjacency matrix for the graph with {V} vertices:”)
for _ in range(V):
row = list(map(int, input().split()))
graph.append(row)
# Print the solution
prim_mst(graph)
Dense Graphs
Definition – Dense graphs are graphs where the number of edges is close to the maximum possible edges between the vertices. In other words, there are relatively many existing connections among the vertices.
Prim’s Algorithm in Dense Graphs
Vertex-Focused Approach
Prim’s algorithm operates by selecting vertices and adding the minimum-weight edges that connect the growing Minimum Spanning Tree (MST) to external vertices.
In dense graphs, where there are many existing edges, the vertex-focused approach of Prim’s algorithm becomes advantageous.
.
Efficiency in Dense Connectivity
As dense graphs have a large number of existing connections, the process of selecting vertices and adding edges becomes more efficient in terms of accessing and updating adjacent vertices.
Prim’s algorithm’s efficiency is less affected by the number of vertices, making it suitable for graphs where there are many edges relative to the number of vertices.
.
Dependence on Starting Vertex
Prim’s algorithm depends on a starting vertex, and it grows the MST from this initial vertex by adding the minimum-weight edges.
In dense graphs, where the connectivity is high, starting from any vertex often leads to a relatively efficient solution.
.
Comparison with Sparse Graphs
In sparse graphs, where the number of edges is much smaller compared to the maximum possible, Prim’s algorithm might become less efficient. This is because the process of growing the MST by selecting vertices and adding edges involves more operations when the graph is not densely connected.
.
Time Complexity of Prim’s Algorithm
The time complexity of Prim’s algorithm depends on the data structure used for implementing the priority queue to efficiently select the minimum edge.
(1) Using Priority Queue with Adjacency List (Binary Heap or Fibonacci Heap)
Binary Heap – O((V + E) * log V)
Fibonacci Heap – O(E + V * log V)
Where, V is the number of vertices, E is the number of edges.
.
(2) Using Priority Queue with Adjacency Matrix (Array or Min Heap)
Using an array – O(V^2)
Using a min heap – O((V + E) * log V)
.
Space Complexity of Prim’s Algorithm
The space complexity of Prim’s algorithm is determined by the data structures used to store information during the algorithm’s execution.
If an adjacency list is used to represent the graph, the space complexity is O(V + E), where V is the number of vertices and E is the number of edges.
If an adjacency matrix is used, the space complexity is O(V^2).
.
Advantages of Prim’s Algorithm
- Guarantees the smallest possible total edge weight.
- Performs well on sparse graphs.
- Conceptually simple and easy to understand
- In the design of integrated circuits and Very Large-Scale Integration (VLSI) systems, it ensures minimizing the interconnection costs.
- Helps in efficiently establishing these connections in robotics and sensor networks.
- Can assist in planning where roads or railways need to be constructed to connect different regions.
- In telecommunication networks, where communication links need to be established, minimizing the total length of connections is essential for cost-effective and efficient communication.
.
Disadvantages of Prim’s Algorithm
- For dense graphs with many edges, the time complexity of the algorithm might be relatively high, especially if using a simple data structure like an adjacency matrix.
- It does not handle graphs with negative cycles. If the graph has a negative cycle, it can’t produce a minimum spanning tree.
Test Yourself
Q1- Can Prim’s algorithm handle disconnected graphs?
Prim’s algorithm assumes the input graph is connected. If the graph is disconnected, the algorithm may not produce a spanning tree that includes all vertices.
Q2- How would adding a constant value to all edge weights in the graph affect Prim’s algorithm?
Adding a constant value to all edge weights doesn’t affect the relative order of the weights. Therefore, the resulting minimum spanning tree would be the same, and only the total weight of the tree would change.
Q3- Can Prim’s algorithm be adapted to handle directed graphs?
Prim’s algorithm is inherently designed for undirected graphs. Adapting it for directed graphs would require modifications, and the resulting algorithm might not guarantee a minimum spanning tree.
Q4- How does introducing negative edge weights in the graph impact Prim’s algorithm?
Prim’s algorithm is not designed to handle graphs with negative edge weights. If negative weights are present, the algorithm may produce incorrect results, and the minimum spanning tree may not be valid.
Q5- Is it possible for Prim’s algorithm to produce different spanning trees for the same graph?
Yes, Prim’s algorithm can produce different minimum spanning trees for the same graph, especially when there are multiple edges with the same minimum weight, and the algorithm has flexibility in choosing between them.
Q6- Which data structure is NOT suitable for implementing the priority queue in Prim’s algorithm?
Binary Heap
Fibonacci Heap
Stack
Min Heap
Ans – (3)
Explanation –
A stack is not suitable for implementing the priority queue in Prim’s algorithm. The priority queue requires efficient extraction of the minimum key, and a stack does not provide this operation in constant time.
Q7- How does the time complexity of Prim’s algorithm change if the graph is represented using an adjacency matrix instead of an adjacency list?
It improves.
It worsens.
It remains the same.
It depends on the number of vertices.
Ans – (2)
Explanation – Using an adjacency matrix result in a time complexity of O(V^2), where V is the number of vertices. This is less efficient than using an adjacency list, which has a time complexity of O((V + E) * log V) with appropriate data structures.
Q8- How to Find Minimum Spanning Tree Using Prim’s Algorithm?
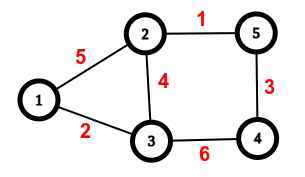
Let’s say vertex 1 is our starting point. You can choose any starting point.
Move 1
Visited Vertex(1) = Edges(5, 2)
We must select minimum weight, So, we choose 2.
The minimum spanning tree is
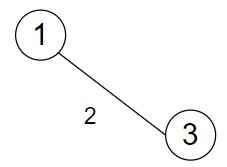
Total weight is 2.
Move 2
Visited Vertex(1, 3) = Edges(5, 4, 6)
We must select minimum weight, So, we choose 4.
The minimum spanning tree is
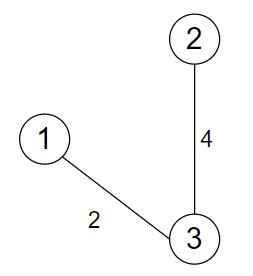
Total weight is 6.
Move 3
Visited Vertex(1, 3, 2) = Edges(1, 6)
We must select minimum weight, So, we choose 1.
The minimum spanning tree is

Total weight is 7.
Move 4
Visited Vertex(1, 3, 2, 5) = Edges(6, 3)
We must select minimum weight, So, we choose 3.
The minimum spanning tree is
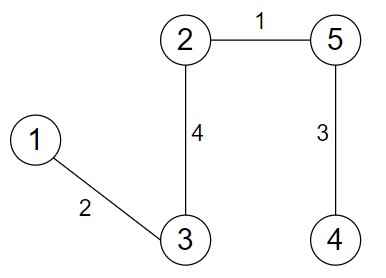
Total weight is 10.
Q9- Using Prim’s algorithm to construct a minimum spanning tree starting with node a, which one of the following sequences of edges represents a possible order in which the edge would be added to construct the minimum spanning tree?
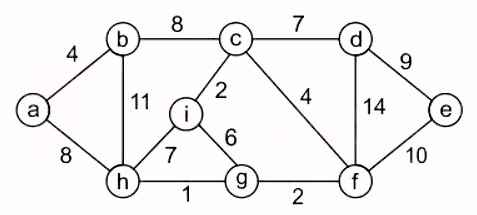
1. (a,b), (b,h), (g,h), (f, g), (c, f), (c, i), (c, d), (d, e)
2. (a,b), (b,c), (c,i), (c, f), (f, g), (g, h), (c, d), (d, e)
3. (a,b), (b,h), (g,h), (g, i), (c, f), (c, i), (c, d), (d, e)
4. (a,b), (g,h), (g,f), (c, f), (c, i), (f, e), (b, c), (d, e)
Ans – (2)
Explanation –

Q10- Prim’s algorithm is also known as __________
Dijkstra–Scholten algorithm
Borůvka’s algorithm
Floyd–Warshall algorithm
DJP Algorithm
Ans – (4)
Explanation – The algorithm was developed by Czech mathematician Vojtín Czernik in 1930 and later by computer scientists Robert C. Prim in 1957 and Edgard W. Dijkstra. Therefore, it is sometimes also called the Járnik algorithm, prim-Járnik algorithm, prime. -Dijkstra algorithm or DJP algorithm.






