P vs NP problem

Introduction

.

In computer science, we often deal with problems that need efficient solutions. Some problems are easy to solve, while others are hard.

The “P vs NP” problem is one of the biggest questions in this field.

It asks: “Can every problem whose solution can be quickly checked (NP) also be quickly solved (P)?” Understanding P and NP is crucial for learning how algorithms work and how to solve problems efficiently.

.

What is P?

“P” stands for Polynomial Time. It refers to problems that can be solved quickly (in polynomial time) by a computer. This means the time it takes to solve the problem grows at a reasonable rate as the problem size increases.

For example, sorting a list of numbers takes O(nlogn) time or finding the shortest path in a graph takes O(E log E) time. The both problems can be done in polynomial time. If a problem is in P, we can solve it efficiently.

.

What is NP?

“NP” stands for Nondeterministic Polynomial Time. These are problems where we cannot necessarily solve them quickly, but if someone gives us a solution, we can check whether it is correct in polynomial time.

An example is the Sudoku puzzle. It might take a long time to solve it, but if someone gives you a completed puzzle, you can easily check if the solution is correct.

.

P vs NP Question

The “P vs NP” problem asks whether every problem that can be checked quickly (NP) can also be solved quickly (P).

In other words, is P equal to NP? This is a famous unsolved problem in computer science. If P = NP, it would mean that all NP problems could be solved just as fast as they can be verified, which would change many things in technology and science. However, most people believe that P ≠ NP, meaning not all problems that are easy to check are easy to solve.

.

Clay Millennium Problems

The Clay Millennium Problems are seven of the most challenging unsolved problems in mathematics, and solving any one of them offers a prize of $1 million from the Clay Mathematics Institute. These problems were announced in the year 2000, and only one has been solved so far.

1. P vs NP Problem
2. Riemann Hypothesis
3. Yang-Mills Existence and Mass Gap
4. Navier-Stokes Existence and Smoothness
5. Hodge Conjecture
6. Birch and Swinnerton-Dyer Conjecture
7. Poincaré Conjecture (Solved) – This problem, originally posed by Henri Poincaré in 1904, asks whether every simply connected, closed 3-dimensional shape is equivalent to a 3-dimensional sphere. It was famously solved by the Russian mathematician Grigori Perelman in 2003 using Ricci flow techniques. He was offered the $1 million prize but declined it.

.

Understanding the P vs NP Problem

Suppose a simple multiplication question is asked.

What is 5 x 17 = ? and,

The answer is 85, you all know that.

Also, a simple factoring question is asked that

What are the factors of 143? and,

The answer is 11 and 13.

.

Let’s try out a bigger multiplication and for doing that multiplication we have to use a powerful tool. A traditional calculator can’t handle very large multiplications due to its digit limit. However, Python programming is a modern and latest tool capable of performing such large calculations within polynomial time.

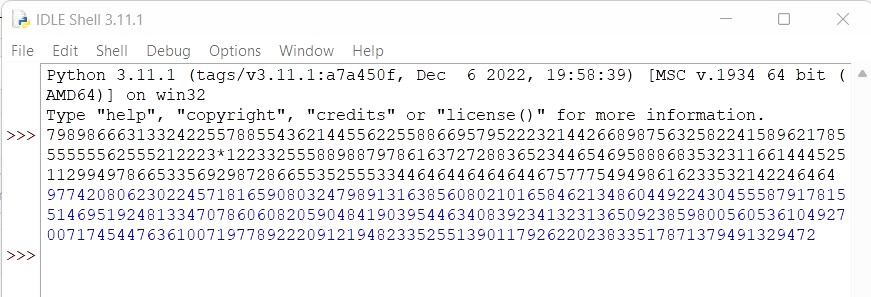
But what is the factoring of a bigger number.

.

The computer can’t list all of the factors of a bigger number in polynomial time.

If we enter 5 digit numbers, the output appears instantly. Similarly, if we enter 6 or 7 digit numbers, the output also comes quickly.

However, when we input 10 digit numbers, the output takes 1 minute 36 seconds.

Assuming the input is 10 and the computer’s speed is 10³ operations per second, we can estimate the time for the output. If it takes approximately 100 seconds, and the computer processes at 10³ operations per second, the output would occur after about 10⁵ operations. The time complexity is about O(n⁵).

.

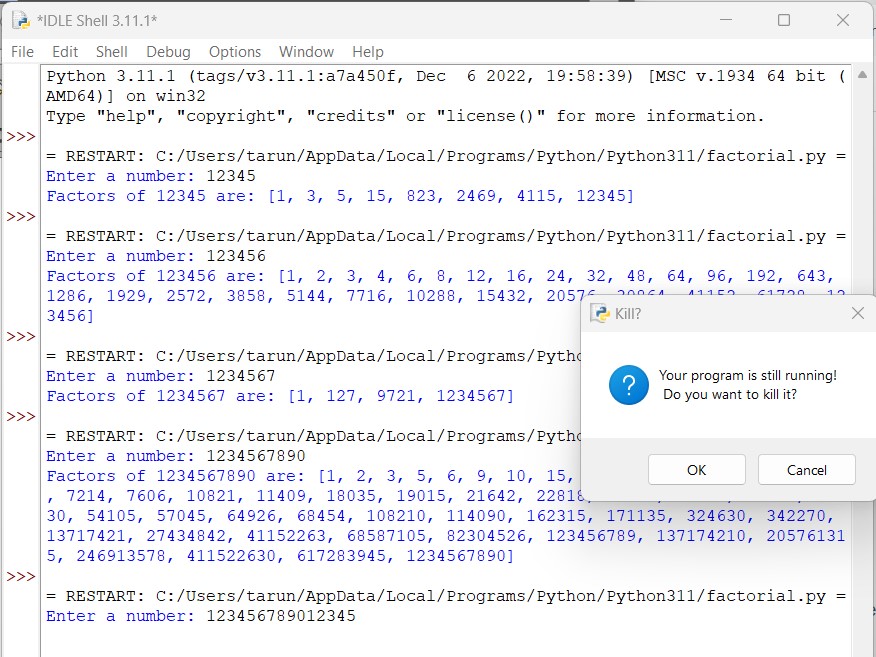
If we input 15 digits number, the result won’t appear for a day and 5 hours. But when I try to close the program, a warning pops up: “Your program is still running! Do you want to kill it?” This means the program is still running and counting the factors, even though the result hasn’t been displayed yet.

So, this is called Non-Deterministic Polynomial Problem.

.

History

The P vs NP problem is a key question in theoretical computer science, and its history can be traced back to the 20th century, when computers were first being studied.

Alan Turing, in 1936, developed the Turing Machine, a simple model that represents how algorithms work. This laid the foundation for understanding which problems can be solved by computers.

In 1950, Gödel, a famous logician, suggested in a letter to John von Neumann that there might be a class of problems where the solutions can be verified quickly (now known as NP), but it’s hard to find the solutions.

Jack Edmonds, in 1965, introduced the idea of “good” algorithms, which could solve problems in polynomial time. This was the birth of the P class.

Stephen Cook, in 1971, formulated the P vs NP problem in a paper titled “The Complexity of Theorem-Proving Procedures.” In this paper, cook defined NP and introduced the concept of NP-completeness. He asked the famous question: “Is P equal to NP?”

Cook showed that many problems in NP are “NP-complete,” meaning they are the hardest problems in NP. If anyone finds an efficient solution for one NP-complete problem, they would be able to solve all NP problems quickly.

Richard Karp, in 1972, He expanded on Cook’s work by identifying 21 NP-complete problems, showing that many real-world problems are in this difficult category.

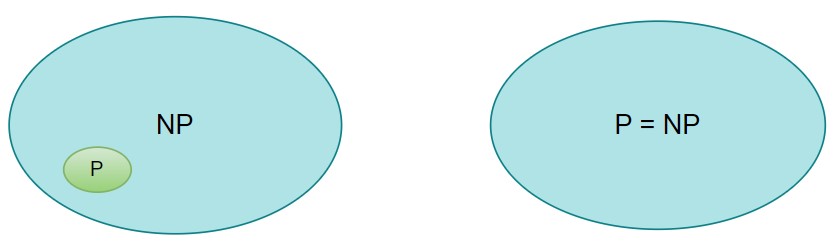
We can’t tell that P = NP. If P and NP were the same, it would mean that any problem for which we can quickly check a solution (in NP) could also be solved quickly (in P). However, most experts believe that P and NP are not the same.

Why? Because for many problems in NP, people have tried very hard to find fast solutions, but no one has succeeded yet. These problems still seem to require slow methods like brute-force search (where every possible solution is tried one by one).

Researchers have also tried to prove that P is not equal to NP, which would mean that no fast algorithm can be found to replace brute-force search. However, this proof has also not been found. So, for now, the question remains open.