Introduction
.
The Nearest Neighbour Problem (NNP) or Traveling Salesman Problem (TSP) by greedy method is a classic algorithmic problem in computer science and operations research.
The goal is simple – “Given a list of cities and the distances between them, find the shortest possible route that visits each city exactly once and returns to the starting point.”
This problem is crucial in fields like logistics, transportation, and manufacturing.
The TSP can be solved using various methods
- Brute Force – Check all possible routes and choose the shortest one. This method guarantees the optimal solution but is impractical for large datasets due to its high computational cost.
- Greedy Algorithms – Heuristics that make local optimal choices at each step to find a global optimum. It is also called Nearest Neighbour Problem.
- Dynamic Programming – Optimizes the problem by solving subproblems and combining their solutions. It is also called Held-Karp algorithm.
- Branch & Bound Approach – breaking the problem into smaller subproblems (branching) and calculating a lower bound for each subproblem. If the lower bound exceeds the current best solution, that branch is pruned (ignored).
- Approximation Algorithms – Provides near-optimal solutions in a reasonable time, useful for large instances. It is also called Christofides Algorithm.
We first solve the Travelling Salesman Problem by Greedy algorithm, that is Nearest Neighbour Problem.
.
Nearest Neighbour Problem Statement
“Given a set of n cities and the distances between every pair of cities, find a tour that visits each city exactly once and returns to the starting city.
The objective is to construct this tour using the Nearest Neighbour Algorithm, aiming to minimize the total distance travelled, though it may not yield the optimal solution.”
.
History
The concept of finding the nearest neighbour likely originates from the study of Voronoi diagrams in the 19th century by mathematicians like Georgy Voronoy. However, the computational aspects of the problem became a focus in the mid-20th century.
During this time, researchers began exploring the problem in the context of geographic information systems (GIS), clustering, and optimization.
In the 1970s, the problem became more formalized with the advent of computational geometry. The introduction of the k-d tree by Jon Bentley in 1975 was a significant breakthrough. The k-d tree is a data structure that allows efficient search for the nearest neighbour in a multidimensional space. During this period, the problem was also studied in operations research, particularly in the context of the Traveling Salesman Problem (TSP). The nearest neighbour heuristic became a popular method for generating approximate solutions to the TSP.
The nearest neighbour search problem also became crucial in machine learning, pattern recognition, and computer vision. For example, in k-nearest neighbours (k-NN) classification, the goal is to classify a data point based on the majority class of its nearest neighbours.
.
Algorithm NearestNeighborTSP(C, D)
Input –
C = {C1, C2, …, Cn} // Set of n cities
D = Distance matrix where D[i][j] is the distance between city Ci and city Cj
1. Let currentCity = C1 // Start from the first city
2. Mark currentCity as visited
3. Initialize tour = [currentCity]
4. Initialize totalDistance = 0
5. While there are unvisited cities
- Find the nearest unvisited city (Minimum Distance)
- Add the distance D[currentCity][nearestCity] to totalDistance
- Move to nearestCity
- Mark nearestCity as visited
- Append nearestCity to tour
- Set currentCity = nearestCity
6. Add the distance D[currentCity][C1] to totalDistance // Return to the starting city
7. Append the starting city C1 to the end of the tour
8. Output tour and totalDistance
.
Example –
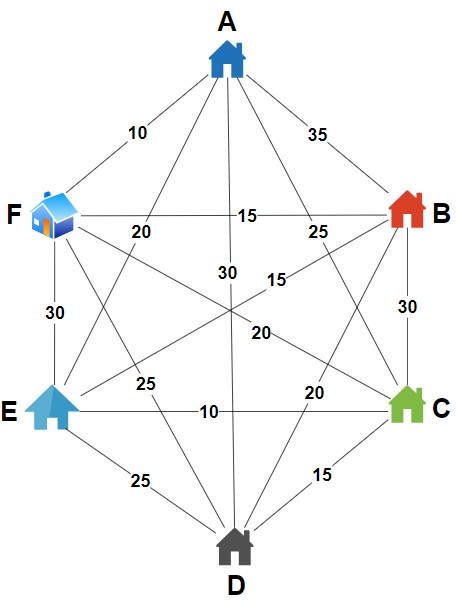
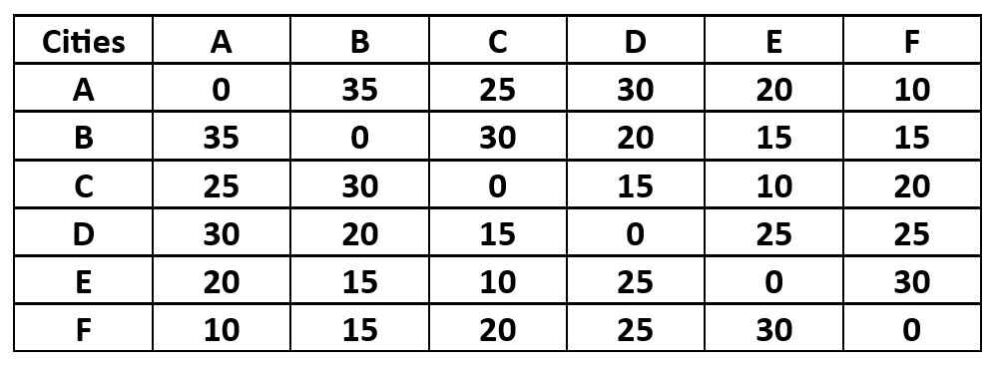
Example Distance Matrix
.
Find a tour that visits each city exactly once and returns to the starting city by always moving to the nearest unvisited city.
Steps
1. Initialization
- Start at City A.
- Mark City A as visited.
- Initialize tour with City A.
2. Iterative Process
- From City A –
- Unvisited cities = B, C, D, E, F
- Distances is A → B = 35, A → C = 25, A → D = 30, A → E = 20, A → F = 10
- Nearest city, F (distance = 10)
- Move to F, mark F as visited.
- Total tour distance = 10
- From City A –
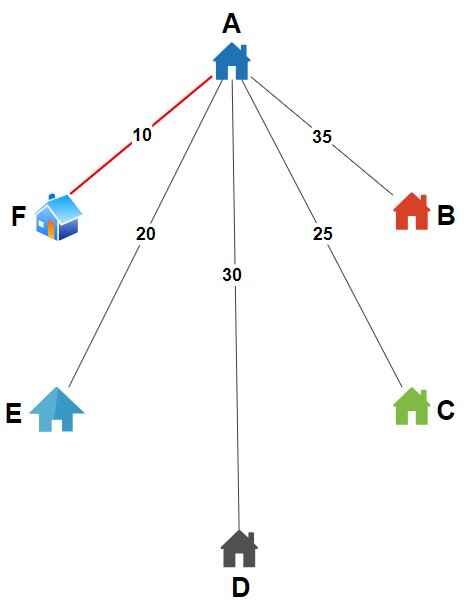
.
- From City F –
- Unvisited cities = B, C, D, E
- Distances is F → B = 15, F → C = 20, F → D = 25, F → E = 30
- Nearest city, B (distance = 15)
- Move to B, mark B as visited.
- Total tour distance = 10 + 15 = 25
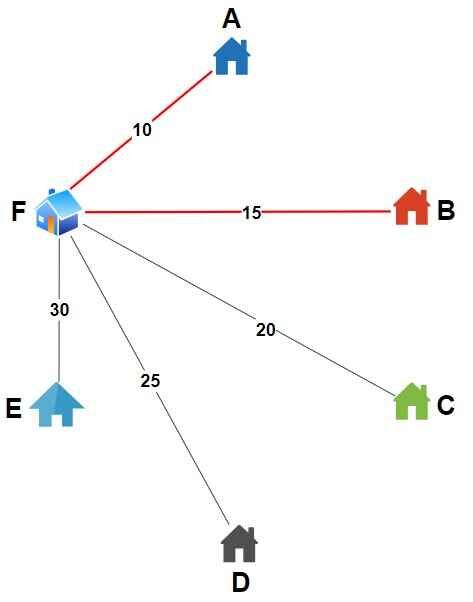
.
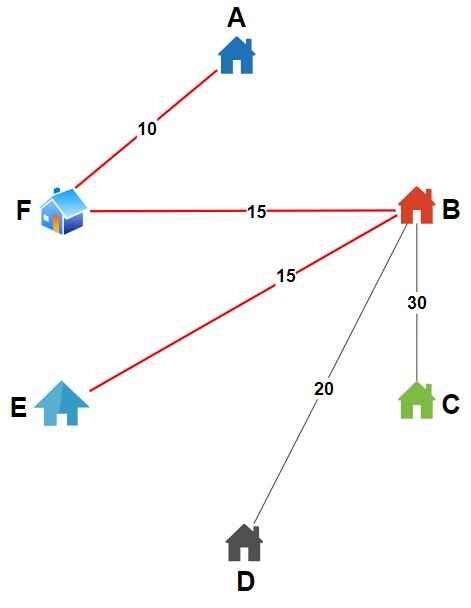
- From City B –
- Unvisited cities = C, D, E
- Distances is B → C = 30, B → D = 20, B → E = 15
- Nearest city, E (distance = 15)
- Move to E, mark E as visited.
- Total tour distance = 25 + 15 = 40
- From City B –
.
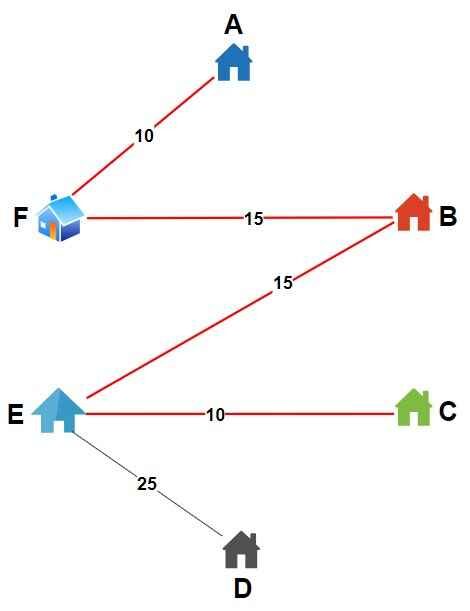
- From City E –
- Unvisited cities = C, D
- Distances is E → C = 10, E → D = 25
- Nearest city, C (distance = 10)
- Move to C, mark C as visited.
- Total tour distance = 40 + 10 = 50
.
- From City C –
- Unvisited city = D
- Distance is C → D = 15
- Move to D, mark D as visited.
- Total tour distance = 50 + 15 = 65
.
3. Returning to starting city A from D
- Distance is D → A = 15
- Final total tour distance = 65 + 30 = 95
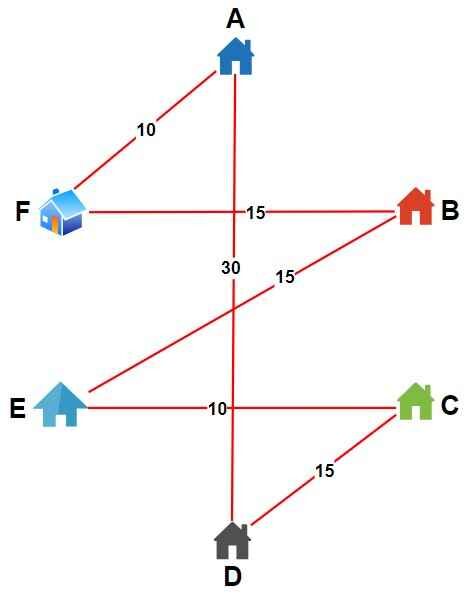
So, our tour is A → F → B → E → C → D → A
This solution demonstrates how the Nearest Neighbour Algorithm works and provides an approximate route based on local decisions at each step.
.
Source Code for Nearest Neighbour Problem
// COMPUTER GEEK – compgeek.co.in
// Write a program for Nearest Neighbour Problem TSP by Greedy Algorithm
#include <stdio.h>
#define MAX_CITIES 100 // Adjust this as needed, or remove if you want to handle dynamically
void nearestNeighbor(int n, int distanceMatrix[MAX_CITIES][MAX_CITIES]) {
int visited[MAX_CITIES] = {0}; // Array to mark visited cities
int tour[MAX_CITIES]; // Array to store the tour
int totalDistance = 0;
int currentCity = 0; // Starting city
int nearestCity;
int i, j;
// Initialize
visited[currentCity] = 1; // Mark the starting city as visited
tour[0] = currentCity;
int tourLength = 1;
// Iterative Process
for (i = 1; i < n; i++) {
int minDistance = 999999; // Large number for comparison
nearestCity = -1;
// Find the nearest unvisited city
for (j = 0; j < n; j++) {
if (!visited[j] && distanceMatrix[currentCity][j] < minDistance) {
minDistance = distanceMatrix[currentCity][j];
nearestCity = j;
}
}
// Move to the nearest city
visited[nearestCity] = 1;
tour[tourLength++] = nearestCity;
totalDistance += minDistance;
currentCity = nearestCity;
}
// Return to the starting city
totalDistance += distanceMatrix[currentCity][0];
tour[tourLength] = 0;
// Output the Tour
printf(“Tour: “);
for (i = 0; i <= tourLength; i++) {
printf(“%d “, tour[i]);
}
printf(“\nTotal Distance: %d\n”, totalDistance);
}
int main() {
int n, i, j;
printf(“Enter the number of cities: “);
scanf(“%d”, &n);
int distanceMatrix[MAX_CITIES][MAX_CITIES];
printf(“Enter the distance matrix:\n”);
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
scanf(“%d”, &distanceMatrix[i][j]);
}
}
nearestNeighbor(n, distanceMatrix);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Nearest Neighbour Problem TSP by Greedy Algorithm
#include <iostream>
const int MAX_CITIES = 100; // Adjust this as needed
void nearestNeighbor(int n, int distanceMatrix[MAX_CITIES][MAX_CITIES]) {
bool visited[MAX_CITIES] = {false}; // Array to mark visited cities
int tour[MAX_CITIES]; // Array to store the tour
int totalDistance = 0;
int currentCity = 0; // Starting city
int nearestCity;
int i, j;
// Initialize
visited[currentCity] = true; // Mark the starting city as visited
tour[0] = currentCity;
int tourLength = 1;
// Iterative Process
for (i = 1; i < n; i++) {
int minDistance = 1000000; // Large number for comparison
nearestCity = -1;
// Find the nearest unvisited city
for (j = 0; j < n; j++) {
if (!visited[j] && distanceMatrix[currentCity][j] < minDistance) {
minDistance = distanceMatrix[currentCity][j];
nearestCity = j;
}
}
// Move to the nearest city
visited[nearestCity] = true;
tour[tourLength++] = nearestCity;
totalDistance += minDistance;
currentCity = nearestCity;
}
// Return to the starting city
totalDistance += distanceMatrix[currentCity][0];
tour[tourLength] = 0;
// Output the Tour
std::cout << “Tour: “;
for (i = 0; i <= tourLength; i++) {
std::cout << tour[i] << ” “;
}
std::cout << “\nTotal Distance: ” << totalDistance << std::endl;
}
int main() {
int n, i, j;
std::cout << “Enter the number of cities: “;
std::cin >> n;
int distanceMatrix[MAX_CITIES][MAX_CITIES];
std::cout << “Enter the distance matrix:\n”;
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
std::cin >> distanceMatrix[i][j];
}
}
nearestNeighbor(n, distanceMatrix);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Nearest Neighbour Problem TSP by Greedy Algorithm
import java.util.Scanner;
public class NearestNeighbor {
static final int MAX_CITIES = 100; // Adjust this as needed
public static void nearestNeighbor(int n, int[][] distanceMatrix) {
boolean[] visited = new boolean[MAX_CITIES]; // Array to mark visited cities
int[] tour = new int[MAX_CITIES]; // Array to store the tour
int totalDistance = 0;
int currentCity = 0; // Starting city
int nearestCity;
int i, j;
// Initialize
visited[currentCity] = true; // Mark the starting city as visited
tour[0] = currentCity;
int tourLength = 1;
// Iterative Process
for (i = 1; i < n; i++) {
int minDistance = Integer.MAX_VALUE; // Large number for comparison
nearestCity = -1;
// Find the nearest unvisited city
for (j = 0; j < n; j++) {
if (!visited[j] && distanceMatrix[currentCity][j] < minDistance) {
minDistance = distanceMatrix[currentCity][j];
nearestCity = j;
}
}
// Move to the nearest city
visited[nearestCity] = true;
tour[tourLength++] = nearestCity;
totalDistance += minDistance;
currentCity = nearestCity;
}
// Return to the starting city
totalDistance += distanceMatrix[currentCity][0];
tour[tourLength] = 0;
// Output the Tour
System.out.print(“Tour: “);
for (i = 0; i <= tourLength; i++) {
System.out.print(tour[i] + ” “);
}
System.out.println(“\nTotal Distance: ” + totalDistance);
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print(“Enter the number of cities: “);
int n = scanner.nextInt();
int[][] distanceMatrix = new int[MAX_CITIES][MAX_CITIES];
System.out.println(“Enter the distance matrix:”);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
distanceMatrix[i][j] = scanner.nextInt();
}
}
nearestNeighbor(n, distanceMatrix);
scanner.close();
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for Nearest Neighbour Problem TSP by Greedy Algorithm
def nearest_neighbor(n, distance_matrix):
visited = [False] * n # Array to mark visited cities
tour = [0] * (n + 1) # Array to store the tour
total_distance = 0
current_city = 0 # Starting city
tour[0] = current_city
visited[current_city] = True
tour_length = 1
# Iterative Process
for _ in range(n – 1):
min_distance = float(‘inf’) # Large number for comparison
nearest_city = -1
# Find the nearest unvisited city
for j in range(n):
if not visited[j] and distance_matrix[current_city][j] < min_distance:
min_distance = distance_matrix[current_city][j]
nearest_city = j
# Move to the nearest city
visited[nearest_city] = True
tour[tour_length] = nearest_city
total_distance += min_distance
current_city = nearest_city
tour_length += 1
# Return to the starting city
total_distance += distance_matrix[current_city][0]
tour[tour_length] = 0
# Output the Tour
print(“Tour:”, ” “.join(map(str, tour)))
print(“Total Distance:”, total_distance)
def main():
n = int(input(“Enter the number of cities: “))
distance_matrix = []
print(“Enter the distance matrix:”)
for _ in range(n):
row = list(map(int, input().split()))
distance_matrix.append(row)
nearest_neighbor(n, distance_matrix)
if __name__ == “__main__”:
main()
Enter the number of cities: 6
Enter the distance matrix:
0 35 25 30 20 10
35 0 30 20 15 15
25 30 0 15 10 20
30 20 15 0 25 25
20 15 10 25 0 30
10 15 20 25 30 0
Tour: 0 5 1 4 2 3 0
Total Distance: 95
=== Code Execution Successful ===
Time Complexity for the Nearest Neighbour Algorithm
Initializing arrays and setting up variables is O(n), where n is the number of cities.
The outer loop runs n times and for each iteration of the outer loop, the inner loop checks all remaining unvisited cities to find the nearest one. This is O(n) in the worst case. Therefore, the time complexity for the iterative process is O(n2).
Returning to the starting city and calculating the total distance are O(n) operations.
Thus, the time complexity of the Nearest Neighbour Algorithm is O(n2).
.
Space Complexity for the Nearest Neighbour Algorithm
The space complexity is O(n) due to the storage required for the visited array and the tour array.
.
Advantages for the Nearest Neighbour Algorithm
- The Nearest Neighbour Algorithm is straightforward to understand and implement. It follows a simple greedy approach, making it a good starting point for solving the Traveling Salesman Problem (TSP).
- With a time-complexity of O(n2), it is relatively fast compared to exact algorithms like dynamic programming, especially for larger numbers of cities.
- Requires minimal computational resources compared to more complex algorithms, making it suitable for scenarios with limited processing power.
.
Disadvantages for the Nearest Neighbour Algorithm
- The Nearest Neighbour Algorithm does not always produce the optimal solution. It can easily get stuck in local optima because it makes a series of local decisions without considering the global context.
- There is no guarantee that the tour produced is the shortest possible. The quality of the solution depends heavily on the starting city and the structure of the distance matrix.
- The final tour can vary significantly based on the starting city. Different starting points might lead to different tour lengths.
- It does not handle constraints such as varying priorities for different cities or specific travel restrictions well.
.
Application for the Nearest Neighbour Algorithm
- Route Planning – Used in applications where a quick, heuristic-based route planning is needed, such as delivery scheduling or logistics where exact solutions are computationally expensive.
- Computer Graphics – Helps in various graphics and optimization problems where heuristic solutions are acceptable, such as optimizing the path for drawing complex shapes or patterns.
- Robotics – Applied in path planning for robots and automated vehicles, where a fast heuristic solution is useful for real-time applications.
- Travel Itinerary Planning – Useful for travel planning applications where a rough estimation of the shortest travel route is required, and an exact solution is not feasible due to time constraints.
- Network Design – Can be used in designing efficient network topologies and minimizing the travel distance or connection length in communication networks.
Test Yourself
Q1- What is the Nearest Neighbour Algorithm, and how is it applied to solve the Traveling Salesman Problem (TSP)?
The Nearest Neighbour Algorithm is a greedy heuristic used to find a solution for the Traveling Salesman Problem (TSP). The algorithm starts at a chosen city and repeatedly moves to the nearest unvisited city until all cities are visited. Finally, it returns to the starting city to complete the tour. This approach aims to minimize the total distance travelled but does not guarantee the optimal solution.
Q2- Discuss the time complexity of the Nearest Neighbour Algorithm.
The time complexity of the Nearest Neighbour Algorithm is O(n2), where n is the number of cities.
This is because for each city, the algorithm searches through all unvisited cities to find the nearest one, which takes O(n) time per city. Since this process is repeated for each city, the overall complexity is O(n2).
Q3- Explain the impact of the starting city on the result of the Nearest Neighbour Algorithm.
The starting city in the Nearest Neighbour Algorithm can significantly impact the final tour length. Since the algorithm is greedy and makes local decisions based on the current city, different starting cities can lead to different tours with varying total distances.
The final result is sensitive to the starting point, and the algorithm might not find the shortest possible tour due to this dependency.
Q4- How does the Nearest Neighbour Algorithm compare to other heuristic methods for solving the TSP, such as the Christofides Algorithm?
The Nearest Neighbor Algorithm is simpler and faster than other heuristic methods like the Christofides Algorithm, which provides better approximations for the TSP.
The Christofides Algorithm guarantees a solution within 3/2 times the optimal tour length, whereas the Nearest Neighbor Algorithm may produce solutions that are significantly longer than the optimal.
While Nearest Neighbor is easier to implement, Christofides offers better performance for finding near-optimal solutions.
Q5- What are some limitations of the Nearest Neighbor Algorithm?
Limitations of the Nearest Neighbor Algorithm include:
Suboptimal Solutions – It often produces solutions that are not the shortest possible tour.
Dependence on Starting Point – The result varies depending on the starting city.
Local Optima – The algorithm may get stuck in local optima without considering the global context.
No Optimality Guarantee – There is no guarantee that the tour will be the shortest one.
Q6- Can the Nearest Neighbor Algorithm be improved to provide better solutions for TSP?
Yes, the Nearest Neighbour Algorithm can be improved by combining it with other methods.
For example, it can be used as a starting point for more advanced algorithms like 2-opt or 3-opt, which refine the initial tour by making local improvements.
Additionally, hybrid approaches that use Nearest Neighbour with optimization techniques or metaheuristics like simulated annealing or genetic algorithms can yield better solutions.
Q7- What is the time complexity of the Nearest Neighbor Algorithm for the Traveling Salesman Problem?
O(nlog n)
O(n2)
O(n3)
O(2n)
Ans – (2)
Explanation – The time complexity is O(n2) due to the need to search through all unvisited cities for each city in the tour.
Q8- In the Nearest Neighbour Algorithm, what is the role of the ‘visited’ array?
To store the distances between cities
To keep track of the total distance travelled
To mark cities that have already been included in the tour
To calculate the optimal tour length
Ans – (3)
Explanation – The ‘visited‘ array keeps track of which cities have been visited to avoid revisiting them.
Q9- What is the primary disadvantage of the Nearest Neighbour Algorithm?
It is too complex to implement.
It always produces the optimal solution.
It may get stuck in local optima.
It has a high time complexity.
Ans – (3)
Explanation – The algorithm may not find the optimal tour due to making only local optimal choices.
Q10- Which of the following is not a method to solve the Traveling Salesman Problem?
Brute Force
Nearest Neighbor Algorithm
Genetic Algorithm
Dijkstra’s Algorithm
Ans – (4)
Explanation – Dijkstra’s Algorithm is used for shortest path problems, not TSP.
Q11- In which case is the Nearest Neighbour Algorithm most likely to perform well?
When the number of cities is very large.
When exact optimal solutions are required.
When a quick, heuristic-based solution is acceptable.
When dealing with complex constraints.
Ans – (3)
Explanation – The Nearest Neighbour Algorithm is useful when a fast, heuristic solution is sufficient.
Q12- What happens if there are ties in the distance between cities in the Nearest Neighbor Algorithm?
The algorithm terminates.
The nearest city is chosen randomly.
All tied cities are visited simultaneously.
The algorithm starts over from the beginning.
Ans – (2)
Explanation – If there are ties in distance, the algorithm typically selects one of the tied cities randomly.






