Introduction
The N-Queen Problem is a well-known challenge in computer science and mathematics.
The problem is named after the queen in chess, which can move any number of squares vertically, horizontally, or diagonally.
The N-Queen Problem is a great way to learn about algorithms, recursion, and backtracking techniques.
.
Problem Statement
The N-Queen Problem involves placing N queens on an N×N chessboard so that no two queens threaten each other. This means:
- No two queens can be in the same row.
- No two queens can be in the same column.
- No two queens can be on the same diagonal.
The objective is to find all possible ways to place the queens on the board while satisfying these constraints. The problem can be generalized to any number of queens, N, and can be solved using various techniques, including the backtracking algorithm.
.
History
The N-Queen Problem is a classic puzzle in the field of combinatorial mathematics and computer science.
It was first proposed in 1848 by the chess player Max Bezzel.
Initially, the problem was posed for 8 queens on an 8×8 chessboard, and it quickly gained attention due to its complexity and elegance.
Over the years, the problem has intrigued many mathematicians and computer scientists, leading to various solutions and methods of exploration. Notable contributions include:
- Gauss (1850) – Carl Friedrich Gauss, a renowned mathematician, was among the first to study the 8-Queen Problem, though he did not publish his findings.
- Jacques Binet (1853) – Binet provided some insights and published a paper on the problem, exploring initial solutions.
- Franz Nauck (1850) – Nauck extended the problem to N queens on an N×N chessboard and published solutions for specific cases.
- Edouard Lucas (1876) – Lucas introduced a method for generating solutions and further popularized the problem through his writings.
- Backtracking Method (20th Century) – With the advent of computers, the backtracking method became a widely used approach to solve the N-Queen Problem. This algorithm efficiently finds all possible solutions by systematically exploring and eliminating invalid positions.
.
Backtracking Approach
A backtracking algorithm is a problem-solving method used to find solutions by exploring all possible options and abandoning those that fail to satisfy the problem’s constraints.
It is particularly useful for solving combinatorial and constraint satisfaction problems.
The key idea is to build a solution incrementally, step by step, and backtrack as soon as it determines that the current path cannot possibly lead to a valid solution.
Here’s how it works
- Choice – Make a choice for the first step of the solution.
- Constraints – Check if this choice violates any constraints.
- If it does, discard this choice and backtrack to the previous step.
- If it doesn’t, proceed to the next step.
- Goal – Continue making choices and checking constraints until a solution is found or all possibilities have been explored.
The process is often visualized as a tree, where each node represents a state of the solution, and branches represent possible choices. If a node leads to a violation of constraints, the algorithm backtracks to the previous node to explore other choices.
.
Algorithm
Here is the basic algorithm for solving the N-Queen problem using backtracking:
- Start with the First Row
- Place a queen in the first column of the first row.
- Check for Safety
- Check if placing the queen in the current position is safe (i.e., it does not share the same column, row, or diagonal with any previously placed queens).
- Recursive Call
- If placing the queen is safe, move to the next row and repeat the process.
- If placing the queen is not safe, try the next column in the current row.
- Backtracking
- If all columns in the current row have been tried and none lead to a solution, backtrack to the previous row and move the queen to the next column.
- Solution Found
- If all queens are placed successfully, the solution is found.
- If all rows are processed and no solution is found, there is no solution for the given N.
Example –
Let’s solve the 4-Queen problem using backtracking.
.
1. Start with 1st row (Extreme Left) & first column (Extreme Top).
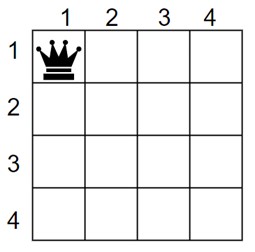
Queen 1 – (1, 1)
.
2. Now, we move to 2nd row and check for safety. If the two queens attack each other, then go for the recursive call and try to move the queen into next cell of the 4×4 chess table.
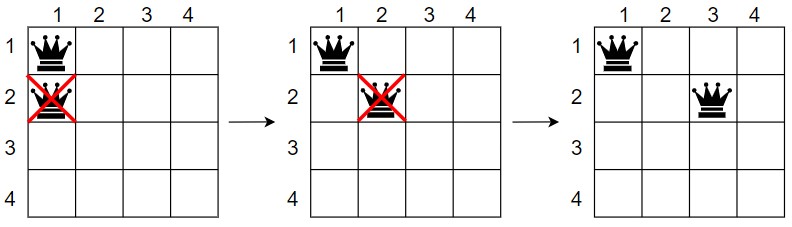
Queen 1 – (1, 1)
Queen 2 – (2, 3)
.
3. Again, we move to the 3rd row and check for safety. If the three queens attack each other, then go for the recursive call and try to move the queen into next cell of 4×4 chess table.
In the 3rd row, there is no cell where the third queen can be placed without the queens attacking each other. So, in the row 2nd, the queen moves into the next cell.
Queen 1 – (1, 1)
Queen 2 – (2, 4)
.
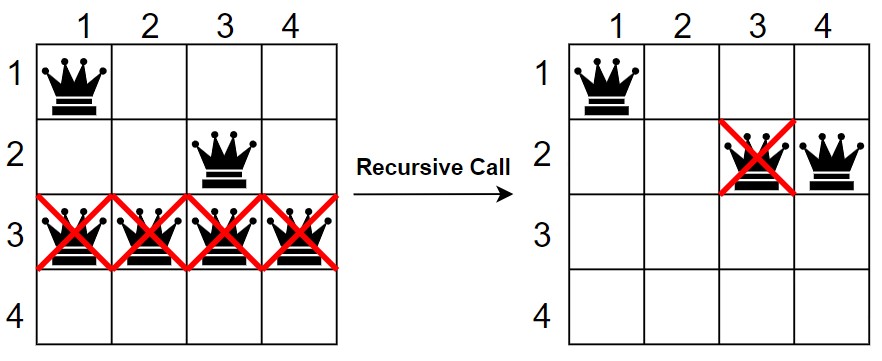
4. Now, in row 3rd, place the third queen and check for safety. The third queen is safe at (3, 2).
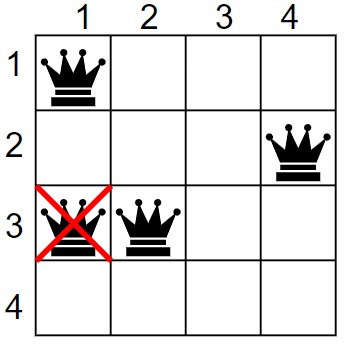
Queen 1 – (1, 1)
Queen 2 – (2, 4)
Queen 3 – (3, 2)
.
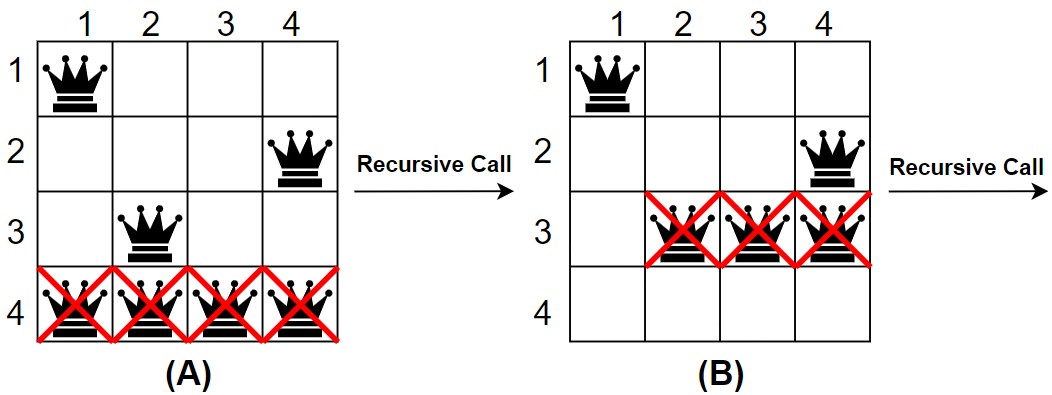
5. Again, we move to the 4th row and check for safety. In the 4th row, there is no cell where the fourth queen can be placed without the queens attacking each other. So, in the row 3rd, the queen moves into the next cell. But, the third queen cannot be placed without queens attacking each other.
.
So, go for 2nd row, and move the queen into the next cell, but it is placed in the last cell of 2nd row. So therefore, go to 1st row, and move the queen into the next cell (1, 2).
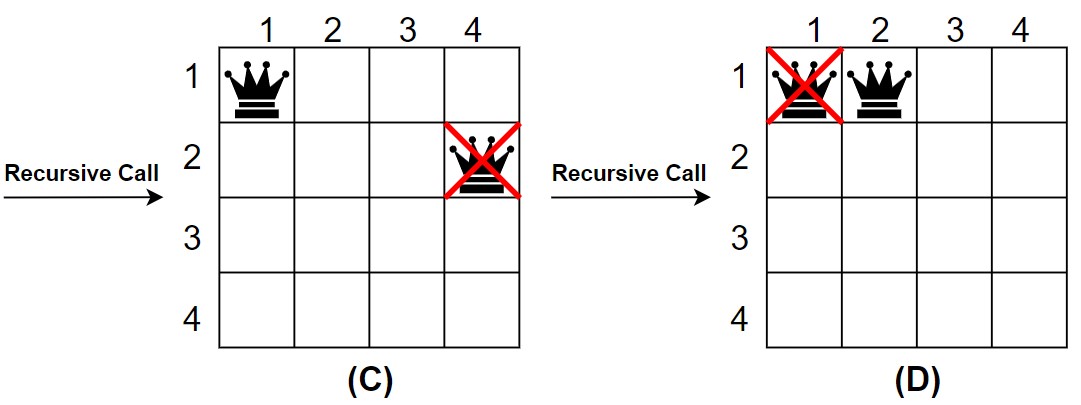
Queen 1 – (1, 2)
.
6. Now, again move to the 2nd row and check for safety. The 2nd queen is safe at (2, 4).
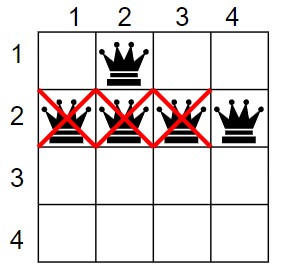
Queen 1 – (1, 2)
Queen 2 – (2, 4)
.
7. Now, move to 3rd row and check for safety. The 3rd queen is safe at (3, 1).
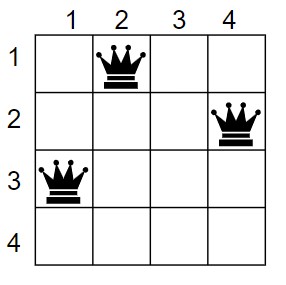
Queen 1 – (1, 2)
Queen 2 – (2, 4)
Queen 3 – (3, 1)
.
8. Now, move to the 4th row and check for safety. The fourth queen is safe at (4, 3).
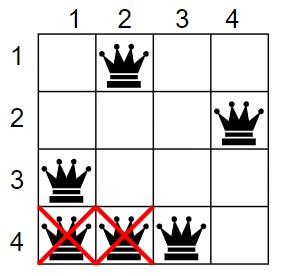
Queen 1 – (1, 2)
Queen 2 – (2, 4)
Queen 3 – (3, 1)
Queen 4 – (4, 3)
.
9. We got the final result through backtracking. Also, you can mirror image the result. Now, you have got two 4×4 Queen solution.
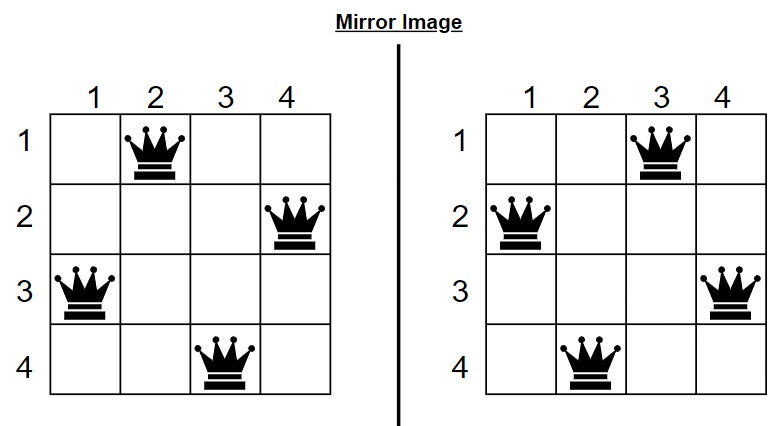
For the 4×4 Queens problem, there are indeed 2 distinct solutions.
.
Source Code of N-Queen Problem
// COMPUTER GEEK – compgeek.co.in
// Write a program for N-Queen Problem
#include <stdio.h>
#include <stdbool.h>
#define MAX 20
int board[MAX][MAX]; // Board to store the positions of queens
// Function to print the board
void printBoard(int N) {
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (board[i][j] == 1)
printf(“Q “);
else
printf(“. “);
}
printf(“\n”);
}
printf(“\n”);
}
// Function to check if it’s safe to place a queen at board[row][col]
bool isSafe(int board[MAX][MAX], int row, int col, int N) {
int i, j;
// Check the column
for (i = 0; i < row; i++)
if (board[i][col] == 1)
return false;
// Check the upper left diagonal
for (i = row, j = col; i >= 0 && j >= 0; i–, j–)
if (board[i][j] == 1)
return false;
// Check the upper right diagonal
for (i = row, j = col; i >= 0 && j < N; i–, j++)
if (board[i][j] == 1)
return false;
return true;
}
// Backtracking function to solve the N-Queens problem
void solveNQueens(int row, int N, int *solutionCount) {
if (row >= N) {
(*solutionCount)++;
printBoard(N);
return;
}
for (int col = 0; col < N; col++) {
if (isSafe(board, row, col, N)) {
board[row][col] = 1; // Place the queen
solveNQueens(row + 1, N, solutionCount); // Recur to place the next queen
board[row][col] = 0; // Backtrack
}
}
}
int main() {
int N;
int solutionCount = 0;
printf(“Enter the number of queens (N): “);
scanf(“%d”, &N);
// Initialize the board with zeros
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
board[i][j] = 0;
printf(“Solutions:\n”);
solveNQueens(0, N, &solutionCount);
printf(“Total solutions: %d\n”, solutionCount);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for N-Queen Problem
#include <iostream>
#include <vector>
using namespace std;
#define MAX 20
vector<vector<int>> board(MAX, vector<int>(MAX, 0));
int solutionCount = 0;
// Function to print the board
void printBoard(int N) {
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (board[i][j] == 1)
cout << “Q “;
else
cout << “. “;
}
cout << endl;
}
cout << endl;
}
// Function to check if it’s safe to place a queen at board[row][col]
bool isSafe(int row, int col, int N) {
int i, j;
// Check the column
for (i = 0; i < row; i++)
if (board[i][col] == 1)
return false;
// Check the upper left diagonal
for (i = row, j = col; i >= 0 && j >= 0; i–, j–)
if (board[i][j] == 1)
return false;
// Check the upper right diagonal
for (i = row, j = col; i >= 0 && j < N; i–, j++)
if (board[i][j] == 1)
return false;
return true;
}
// Backtracking function to solve the N-Queens problem
void solveNQueens(int row, int N) {
if (row >= N) {
solutionCount++;
printBoard(N);
return;
}
for (int col = 0; col < N; col++) {
if (isSafe(row, col, N)) {
board[row][col] = 1; // Place the queen
solveNQueens(row + 1, N); // Recur to place the next queen
board[row][col] = 0; // Backtrack
}
}
}
int main() {
int N;
cout << “Enter the number of queens (N): “;
cin >> N;
cout << “Solutions:\n”;
solveNQueens(0, N);
cout << “Total solutions: ” << solutionCount << endl;
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for N-Queen Problem
import java.util.Scanner;
public class NQueens {
private static int[][] board;
private static int solutionCount = 0;
// Function to print the board
private static void printBoard(int N) {
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (board[i][j] == 1)
System.out.print(“Q “);
else
System.out.print(“. “);
}
System.out.println();
}
System.out.println();
}
// Function to check if it’s safe to place a queen at board[row][col]
private static boolean isSafe(int row, int col, int N) {
int i, j;
// Check the column
for (i = 0; i < row; i++)
if (board[i][col] == 1)
return false;
// Check the upper left diagonal
for (i = row, j = col; i >= 0 && j >= 0; i–, j–)
if (board[i][j] == 1)
return false;
// Check the upper right diagonal
for (i = row, j = col; i >= 0 && j < N; i–, j++)
if (board[i][j] == 1)
return false;
return true;
}
// Backtracking function to solve the N-Queens problem
private static void solveNQueens(int row, int N) {
if (row >= N) {
solutionCount++;
printBoard(N);
return;
}
for (int col = 0; col < N; col++) {
if (isSafe(row, col, N)) {
board[row][col] = 1; // Place the queen
solveNQueens(row + 1, N); // Recur to place the next queen
board[row][col] = 0; // Backtrack
}
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print(“Enter the number of queens (N): “);
int N = scanner.nextInt();
board = new int[N][N];
System.out.println(“Solutions:”);
solveNQueens(0, N);
System.out.println(“Total solutions: ” + solutionCount);
scanner.close();
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for N-Queen Problem
def print_board(board):
N = len(board)
for i in range(N):
for j in range(N):
if board[i][j] == 1:
print(“Q “, end=””)
else:
print(“. “, end=””)
print()
print()
def is_safe(board, row, col, N):
# Check the column
for i in range(row):
if board[i][col] == 1:
return False
# Check the upper left diagonal
i, j = row, col
while i >= 0 and j >= 0:
if board[i][j] == 1:
return False
i -= 1
j -= 1
# Check the upper right diagonal
i, j = row, col
while i >= 0 and j < N:
if board[i][j] == 1:
return False
i -= 1
j += 1
return True
def solve_nqueens(board, row, N, solution_count):
if row >= N:
solution_count[0] += 1
print_board(board)
return
for col in range(N):
if is_safe(board, row, col, N):
board[row][col] = 1 # Place the queen
solve_nqueens(board, row + 1, N, solution_count) # Recur to place the next queen
board[row][col] = 0 # Backtrack
def main():
N = int(input(“Enter the number of queens (N): “))
board = [[0] * N for _ in range(N)]
solution_count = [0]
print(“Solutions:”)
solve_nqueens(board, 0, N, solution_count)
print(f”Total solutions: {solution_count[0]}”)
if __name__ == “__main__”:
main()
Enter the number of queens (N): 4
Solutions:
. Q . .
. . . Q
Q . . .
. . Q .
. . Q .
Q . . .
. . . Q
. Q . .
Total solutions: 2
=== Code Execution Successful ===
Time Complexity of N-Queen Problem
The backtracking algorithm can be described as having a worst-case time complexity of O(N!). This is because there are N choices for the first queen, N-1 for the second, N-2 for the third, and so on, leading to N! permutations to explore in the worst case.
The backtracking algorithm includes checks (pruning) to avoid configurations that are invalid early on. These checks can significantly reduce the number of recursive calls compared to the worst-case scenario. The Best-Case Time Complexity O(N2) (with effective pruning and optimizations).
.
Space Complexity of N-Queens Problem
The space needed to store the N x N chessboard or the current configuration of queens on the board. This requires O(N2) space.
.
Application of N-Queen Problem
- Scheduling Problems
In scheduling tasks or events, you often need to ensure that no two tasks overlap or conflict. The N-Queens problem’s approach of placing queens in such a way that they don’t threaten each other is similar to ensuring that no tasks in a schedule conflict with each other.
.
- Resource Allocation
When managing resources, such as assigning workers to tasks or jobs, you want to ensure that no two resources are assigned to the same task or job at the same time. The N-Queens problem’s method of placing queens so that they don’t interfere with each other can be adapted to prevent resource conflicts.
.
- Puzzle Games
In game development, similar techniques are used to design puzzles where players must place items or pieces on a board without causing conflicts or overlaps. The principles of the N-Queens problem can help in creating and solving these types of puzzles.
.
Optimization Problems
Many optimization problems involve placing or arranging objects in a way that maximizes efficiency or minimizes conflicts. The N-Queens problem is an example of how to systematically explore all possible configurations to find the optimal solution.
.
- AI and Machine Learning
In AI, especially in game development and simulation, algorithms like the one used for the N-Queens problem help in making decisions where constraints must be met. The techniques can be adapted for more complex decision-making processes where different constraints need to be balanced.
Test Yourself
Q1- What is the N-Queen Problem, and why is it important in computer science?
The N-Queen Problem involves placing N queens on an N×N chessboard so that no two queens can attack each other.
It is important in computer science as it serves as a classic example for studying algorithms, particularly backtracking, and helps in understanding constraint satisfaction and combinatorial problems.
Q2- Describe the backtracking approach used to solve the N-Queen Problem.
Backtracking involves placing queens one by one in different columns of a row. It checks if the placement is safe from attacks.
If placing a queen leads to a conflict, it removes the queen (backtracks) and tries the next possible position. This process continues recursively until all queens are placed or all options are exhausted.
Q3- What are the constraints that must be satisfied in the N-Queen Problem?
The constraints are –
- No two queens can be in the same row.
- No two queens can be in the same column.
- No two queens can be on the same diagonal (both primary and secondary).
Q4- Explain how the time complexity of the backtracking algorithm is determined for the N-Queen Problem.
The time complexity of the backtracking algorithm for the N-Queen Problem is determined by the number of possible permutations of queen placements. In the worst case, it explores N! permutations, leading to a time complexity of O(N!).
However, effective pruning and constraint checks can reduce the number of recursive calls, optimizing the performance.
Q5- What are the major advantages of using the backtracking method to solve the N-Queen Problem?
The main advantages include –
- Systematic exploration of solutions.
- Ability to handle large N values by pruning invalid configurations early.
- Clear and understandable algorithmic approach.
Q6- What are some limitations of the backtracking method for solving the N-Queen Problem?
- Potentially high time complexity for large N due to factorial growth.
- The algorithm may be inefficient without effective pruning and optimization.
- High space usage due to recursion and storage of the board.
Q7- How does the N-Queen Problem relate to real-world applications like scheduling or resource allocation?
The N-Queen Problem’s constraint satisfaction approach is similar to scheduling tasks or allocating resources where conflicts must be avoided.
For example, ensuring no two tasks overlap or no two resources are assigned to the same task.
Q8- Compare the backtracking approach with other techniques for solving the N-Queen Problem.
Compared to brute force, backtracking is more efficient as it prunes invalid configurations early.
Dynamic programming and constraint propagation techniques, such as constraint satisfaction problems (CSPs), can offer more optimized solutions for larger N, but backtracking remains a fundamental approach for understanding recursive problem-solving.
Q9- What is the significance of the historical contributions to the N-Queen Problem, and how have they influenced modern algorithms?
Historical contributions by mathematicians like Gauss, Binet, and Lucas helped formalize the problem and explore initial solutions.
Their work laid the groundwork for modern algorithms, including backtracking, which efficiently finds solutions and has influenced approaches to other combinatorial and constraint satisfaction problems.
Q10- What is the time complexity of the backtracking algorithm for the N-Queen Problem?
O(N)
O(N^2)
O(N!)
O(2^N)
Ans – (3)
Explanation – The worst-case time complexity due to exploring all permutations.
Q11- Which data structure is primarily used to store the board configuration in the N-Queen Problem?
Array
Linked List
Stack
Queue
Ans – (1)
Explanation – A 2D array is used to represent the chessboard.
Q12- How many distinct solutions exist for the 8-Queen Problem?
16
24
64
92
Ans – (4)
Explanation – There are exactly 92 distinct solutions.
Q13- What is the space complexity of the backtracking algorithm for the N-Queen Problem?
O(N)
O(N^2)
O(N^3)
O(2^N)
Ans – (2)
Explanation – Space for the board and recursion stack.
Q14- Which technique is commonly used to improve the efficiency of the backtracking algorithm for the N-Queen Problem?
Randomization
Memoization
Pruning
Greedy Method
Ans – (3)
Explanation – Pruning helps eliminate invalid configurations early.
Q15- Who first proposed the N-Queen Problem?
Carl Friedrich Gauss
Max Bezzel
Jacques Binet
Edouard Lucas
Ans – (2)
Explanation – It was first proposed in 1848 by the chess player Max Bezzel.
Initially, the problem was posed for 8 queens on an 8×8 chessboard, and it quickly gained attention due to its complexity and elegance.
Q16- Which of the following is a real-world application of the N-Queen Problem?
Text searching
Graph coloring
Scheduling tasks
Sorting data
Ans – (3)
Explanation – Similar constraint satisfaction is used in scheduling.






