Definition
A Minimum Spanning Tree (MST) is a fundamental concept in graph theory and network design.
“It refers to a tree-like subgraph of a given connected graph that connects all its vertices with the minimum possible total edge weight.”
.
A Minimum Spanning Tree is a subgraph of a connected graph that
1. Contains all the vertices of the graph.
2. Is a tree, which means it has no cycles or loops.
3. Has the minimum possible total sum of edge weights among all such subgraphs.
.
Suppose ABCD is a graph.

.
G(V, E) represents the above graph, where ‘V‘ is the number of vertices and ‘E‘ is the number of edges.
The number of spanning trees in a complete graph with n vertices, often denoted as Kn, can be calculated using Cayley’s formula. Cayley’s formula states that the number of spanning trees in a complete graph with n vertices is equal to n(n-2).
Cayley’s formula K4 = 4(4-2) = 16
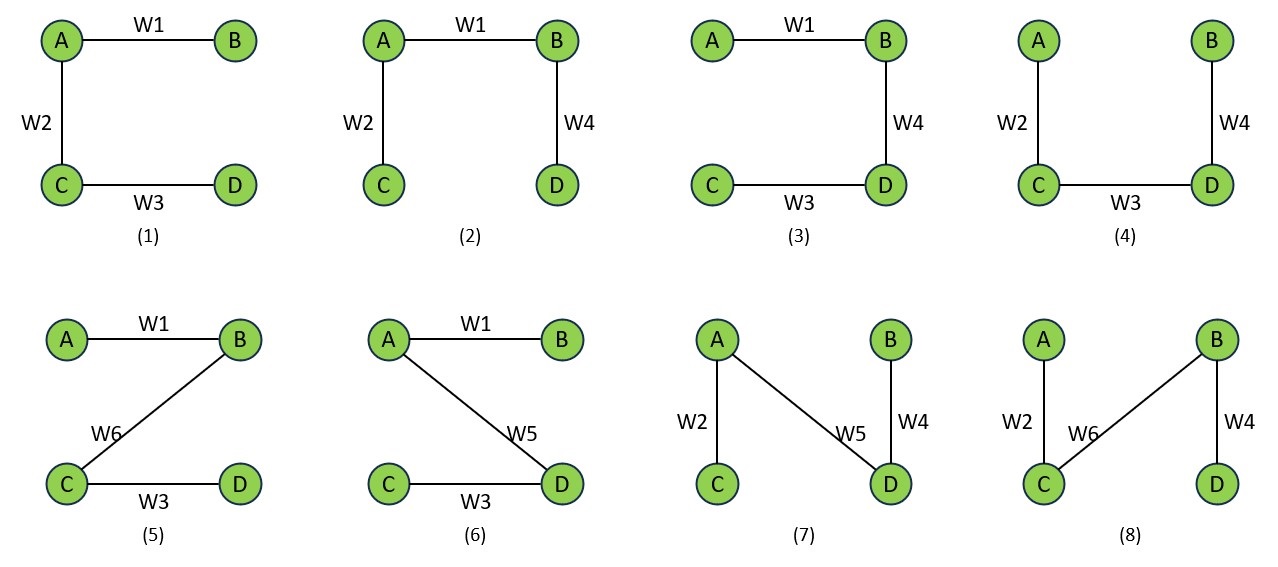
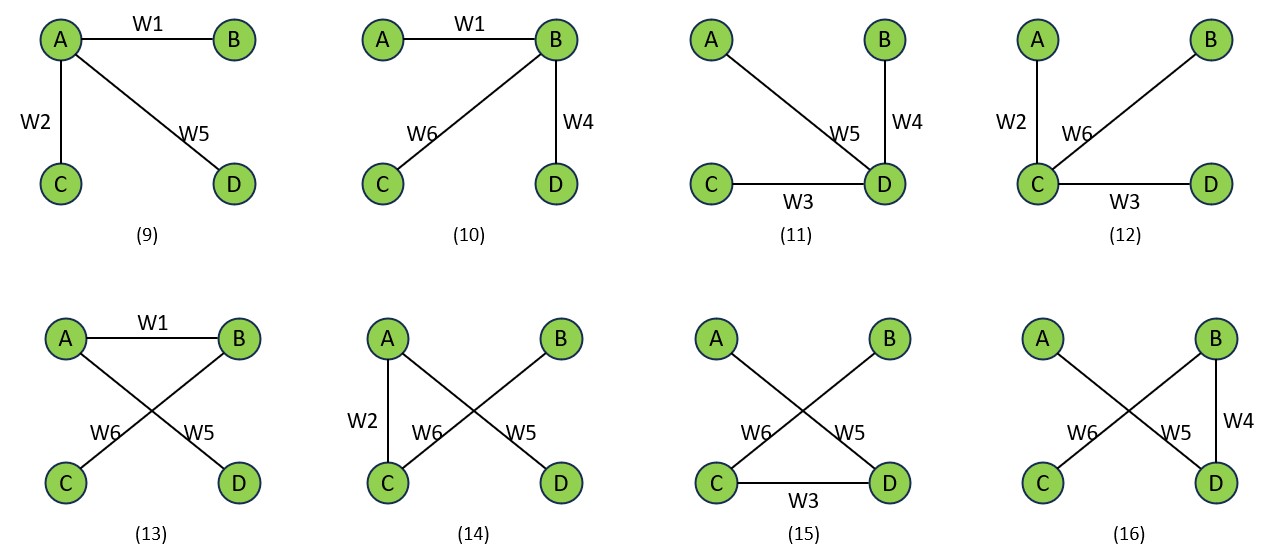
.
There are 16 spanning trees and the weights decide the minimum spanning tree.
The tree with minimum sum of weights is called the minimum spanning tree (MST).
- The above graph’s spanning tree would be stated as ST(V’, E’).
- In this situation, V’ = V denotes that the number of vertices in the spanning tree is equal to the number of vertices in the graph, but the number of edges is different.
- The number of edges must be E’ = V – 1, because edges is one less than the vertices.
- Also, if you create a spanning tree in a complete graph, then you must remove some edges. So, the maximum number of edges can be removed is equal to E – V + 1.
In our example, the edges is 6, the vertices are 4, so we can remove 6 – 4 + 1 edges = 3 edges.
.
Different Algorithms of Minimum Spanning Tree
- Prim’s Algorithm – It starts with an arbitrary vertex and grows the minimum spanning tree one vertex at a time by adding the shortest edge that connects a vertex in the tree to a vertex outside the tree.
- Kruskal’s Algorithm – It starts with an empty set of edges and adds the edges with the smallest weights while avoiding the creation of cycles. It’s based on sorting edges by weight.
Prim’s & Kruskal’s algorithm is greedy in nature.
.
Time Complexity of Minimum Spanning Tree (MST)
The time complexity of finding the minimum spanning tree (MST) depends on the algorithm used. Two commonly used algorithms for finding the minimum spanning tree are Kruskal’s algorithm and Prim’s algorithm.
In both the algorithm, the time complexity is O(E log E) or O(E log V), where E is the number of edges and V is the number of vertices.
.
Advantages of Minimum Spanning Tree (MST)
- MST helps find the most cost-effective way to connect points. It’s like figuring out the cheapest and most efficient routes between different locations.
- It ensures that all points (like cities or nodes in a network) are connected in the most efficient way possible, minimizing the total distance or cost of connections.
- MST avoids creating unnecessary loops or redundant paths.
- In computer networks or communication systems, MST helps design efficient connections, reducing delays and ensuring smooth communication between devices.
- By selecting the minimum necessary connections, MST helps conserve resources such as time, energy, and materials.
.
Disadvantages of Minimum Spanning Tree (MST)
- There can be multiple MSTs for the same graph if there are edges with the same weight. This lack of uniqueness might complicate decision-making in certain applications.
- MSTs are typically calculated based on static data, assuming fixed edge weights (travel times in the case of Google Maps). However, real-world conditions are dynamic and subject to change (e.g., accidents, road closures, traffic congestion).
- For large graphs, finding the MST can become computationally expensive.
- MST algorithms assume that the distance (or weight) between two points is the same in both directions. For example, if the distance from point A to point B is X, then the distance from point B to point A is also X. But in some real-world scenarios, distances may not be symmetric.
.
Applications of Minimum Spanning Tree (MST)
1. Network Design
In communication networks, such as telephone or computer networks, MSTs help design the most efficient and cost-effective way to connect different locations or devices.
2. Cluster Analysis
MSTs can be used in clustering analysis to identify natural groupings or clusters within a set of data points.
3. Circuit Design
In electronic circuit design, MSTs assist in connecting components with minimal wire length, reducing the overall cost and improving the efficiency of the circuit.
4. Transportation Planning
MSTs can model transportation networks, helping in planning routes for vehicles or designing efficient delivery networks.
6. Resource Management
In resource management, such as water or power distribution systems, MSTs can help determine the most efficient way to connect various distribution points.
7. Image Segmentation
In image processing, MSTs are used for segmentation to identify distinct regions or objects within an image.
8. Robotics and Sensor Networks
MSTs are applied in robotics and sensor networks for efficient data transmission and communication. They help optimize the connectivity of sensors or robots in a network.
9. Approximation Algorithms
MSTs are fundamental in designing approximation algorithms for solving complex optimization problems. For example, the famous Traveling Salesman Problem (TSP) can be approximated using MSTs.
10. VLSI Design
Very Large Scale Integration (VLSI) design involves placing and connecting components on a chip. MSTs can be used to minimize the total wire length, improving the performance and reliability of the design.
11. Spanning Tree Protocol
The Spanning Tree Protocol (STP) used in computer networks is a distributed algorithm that creates a loop-free topology.
Test Yourself
Q1- Explain why having multiple Minimum Spanning Trees for the same graph is possible. Provide an example to illustrate your answer.
Multiple Minimum Spanning Trees are possible when there are edges with the same weight.

This graph contains two Minimum Spanning Trees both have weight 7.
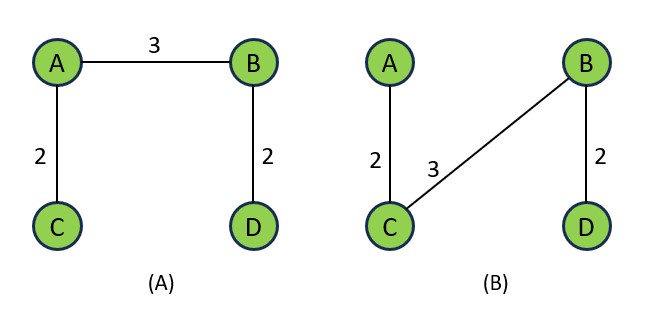
Q2- Discuss a real-world scenario where the assumption of symmetric distances in MSTs might not hold. How could this impact the accuracy of the Minimum Spanning Tree?
In transportation systems, the time or cost to travel from point A to point B might not be the same as from point B to point A due to traffic conditions or road quality. Ignoring this asymmetry could lead to suboptimal solutions in MSTs.
Q3- Consider a scenario where edge weights in a graph are subject to frequent fluctuations. How does this affect the stability and reliability of the Minimum Spanning Tree over time?
Fluctuating edge weights can lead to frequent changes in the Minimum Spanning Tree, making it less stable and reliable. This instability could be a significant drawback in scenarios requiring a consistent and dependable network structure.
Q4- Can there be a situation where the Minimum Spanning Tree is not the most efficient way to connect points in a graph? Provide an example to support your explanation.
Yes, in cases where indirect routes may be more efficient than the implied direct connections in MSTs. For example, in a transportation network, a longer but faster road might be overlooked.
Q5- Discuss a scenario where the removal of an edge in a graph to create a minimum spanning tree might impact the overall connectivity and efficiency.
Consider a scenario where a graph has two disconnected components. To create an MST, we need to include a bridge edge that connects these components.
If we neglect the bridge edge, the resulting structure would be a forest of trees, not a single spanning tree.
Q6- Discuss a scenario where the uniqueness of the Minimum Spanning Tree is crucial. How might the existence of multiple MSTs impact the decision-making process in that situation?
In critical systems like power distribution, having multiple MSTs could lead to uncertainties in planning, maintenance, and decision-making, making it crucial to ensure a unique solution.
Q7- What is the significance of a Minimum Spanning Tree (MST) in network design?
It maximizes the number of edges.
It minimizes the total edge weight.
It creates cycles in the graph.
It connects only a subset of vertices.
Ans – (2)
Explanation – The primary goal of an MST is to connect all vertices with the minimum possible total edge weight.
Q8- Which algorithm starts with an empty set of edges and adds the edges with the smallest weights while avoiding the creation of cycles?
Prim’s Algorithm
Kruskal’s Algorithm
Dijkstra’s Algorithm
Bellman-Ford Algorithm
Ans – (2)
Explanation – Kruskal’s algorithm is a greedy algorithm that starts with an empty set and adds edges with the smallest weights without creating cycles.
Q9- How many spanning trees are there in a complete graph with 5 vertices, according to Cayley’s formula?
50
100
150
125
Ans – (4)
Explanation – Cayley’s formula states that the number of spanning trees in a complete graph with n vertices is equal to nn-2.
For n=5, it’s 55-2 = 125.
Q10- In a complete graph with 5 vertices, how many edges can be removed to create a spanning tree?
6
5
3
4
Ans – (1)
Explanation –
The maximum number of edges in a complete graph with n vertices is n(n-1)/2 = 5*4/2 = 10
The maximum number of edges that can be removed in a complete graph with n vertices to create a spanning tree is E – V + 1. For n=5, it’s 10 – 5 + 1 = 6.
Q11- What is the time complexity of finding the Minimum Spanning Tree using Kruskal’s or Prim’s algorithms?
O(V)
O(E)
O(EV)
O(E log V)
Ans – (4)
Explanation – Both Kruskal’s and Prim’s algorithms have a time complexity of O(E log E) or O(E log V), where E is the number of edges and V is the number of vertices.
Q12- What advantage does a Minimum Spanning Tree offer in network design?
Maximizes redundancy
Minimizes resource usage
Creates loops for flexibility
Maximizes the number of disconnected components
Ans – (2)
Explanation – MSTs help design the most efficient way to connect points, minimizing the total distance or cost of connections.






