Matrix Chain Multiplication

Introduction

.

Matrix Chain Multiplication is a classic problem in computer science and operations research. The goal is to determine the most efficient way to multiply a given sequence of matrices. The problem does not involve performing the actual multiplications but rather determining the order of multiplications that minimizes the total number of scalar multiplications.

.

Working

When multiplying multiple matrices, the order in which the matrices are multiplied can significantly affect the number of operations required.

For example, given three matrices A, B, and C, the product can be computed in two different ways: (AB)C or A(BC).

Each way requires a different number of operations. The Matrix Chain Multiplication problem seeks the optimal order of multiplication for a given sequence of matrices to minimize these operations.

.

First off, it should be noted that matrix multiplication is associative, but not commutative. But since it is associative, we always have:

((AB)(CD)) = (A(B(CD)))

or equality for any such grouping as long as the matrices in the product appear in the same order.

.

It may appear on the surface that the amount of work done won’t change if you change the parenthesizing of the expression, but we can prove that is not the case with the following example:

Let A be a 2×10 matrix

Let B be a 10×50 matrix

Let C be a 50×20 matrix

.

Consider computing A(BC) –

Number of multiplications for (BC) = 10x50x20 = 10000, creating a 10×20 answer matrix

Number of multiplications for A(BC) = 2x10x20 = 400,

Total multiplications = 10000 + 400 = 10400.

.

Consider computing (AB)C –

Number of multiplications for (AB) = 2x10x50 = 1000, creating a 2×50 answer matrix

Number of multiplications for (AB)C = 2x50x20 = 2000,

Total multiplications = 1000 + 2000 = 3000, a significant difference.

Thus, the (AB)C is the winner because the goal to multiply the fewest number of multiplications necessary to compute the product.

.

Dynamic Programming Approach

The Matrix Chain Multiplication (MCM) problem is indeed solved using dynamic programming.

This approach efficiently finds the optimal order of matrix multiplications by breaking the problem into smaller subproblems, solving each subproblem once, and storing the solutions for future reference.

This method avoids redundant calculations and significantly reduces the time complexity compared to a naive approach.

.

We have a recursive formula –

N[i][j] = min value of N[i][k] + N[k+1][j] + d[i]d[k+1]d[j+1], over all valid values of k.

Where N[i][j] is the minimum number of multiplications needed to multiply matrices from A[i] to A[j], d[] represents the dimension.

Smaller problems need to be solved before larger ones.

For example, we need to know N[i][i+1] the number of multiplications to multiply any adjacent pair of matrices, before moving on to larger tasks.

Next, we solve for all values of the form N[i][i+2], then N[i][i+3]​, and so on. Here is the algorithm –

.

Algorithm of MCM by Dynamic Programming Approach

1. Initialize N[i][i] = 0 and all other entries in N to ∞.
2. Loop through the chain lengths
   • For i = 1 to n−1
     • For j=0 to n−1−i:
       1. For k = j to j + i − 1:
          1. If N[j][j+i−1] > N[j][k] + N[k+1][j+i−1] + d[j]d[k+1]d[i+j]
             • Update N[j][j+i−1] = N[j][k] + N[k+1][j+i−1] + d[j]d[k+1]d[i+j​]

This way, we solve the smaller sub-problems first, gradually building up to the solution for the entire chain.

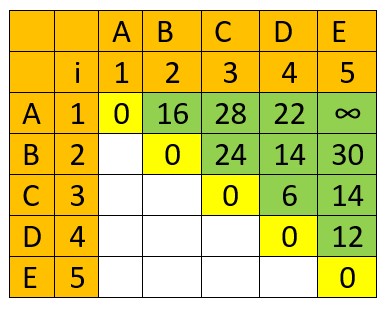
Example –

Initialize N[i][i] = 0 and all other entries in N to ∞.

.

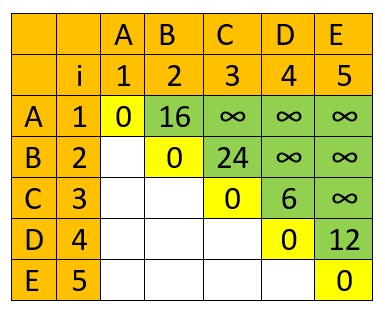
First, we determine the number of multiplications necessary for 2 matrices –

A x B uses 2 x 4 x 2 = 16 multiplications

B x C uses 4 x 2 x 3 = 24 multiplications

C x D uses 2 x 3 x 1 = 6 multiplications

D x E uses 3 x 1 x 4 = 12 multiplications

.

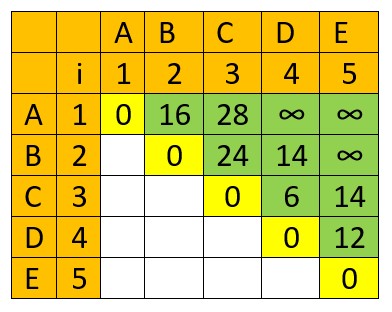
Now, let’s determine the number of multiplications necessary for 3 matrices

(A x B) x C uses 16 + 0 + 2x2x3 = 28 multiplications

A x (B x C) uses 0 + 24 + 2x4x3 = 48 multiplications,

so 28 is min.

.

(B x C) x D uses 24 + 0 + 4x3x1 = 36 multiplications

B x (C x D) uses 0 + 6 + 4x2x1 = 14 multiplications,

so 14 is min.

.

(C x D) x E uses 6 + 0 + 2x1x4 = 14 multiplications

C x (D x E) uses 0 + 12 + 2x3x4 = 36,

so 14 is min.

.

Four matrices next –

A x (B x C x D) uses 0 + 14 + 2x4x1 = 22 multiplications

(A x B) x (C x D) uses 16 + 6 + 2x2x1 = 26 multiplications

(A x B x C) x D uses 28 + 0 + 2x3x1 = 34 multiplications

So, 22 is min.

B x (C x D x E) uses 0 + 14 + 4x2x4 = 46 multiplications

(B x C) x (D x E) uses 24 + 12 + 4x3x4 = 84 multiplications

(B x C x D) x E uses 14 + 0 + 4x1x4 = 30 multiplications

So, 30 is min.

.

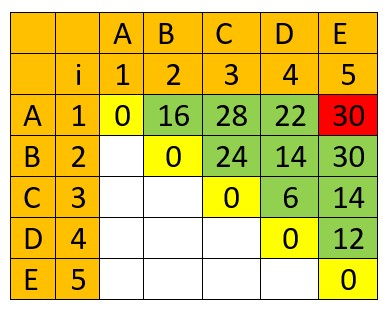
For the answer –

A x (B x C x D x E) uses 0 + 30 + 2x4x4 = 62 multiplications

(A x B) x (C x D x E) uses 16 + 14 + 2x2x4 = 46 multiplications

(A x B x C) x (D x E) uses 28 + 12 + 2x3x4 = 64 multiplications

(A x B x C x D) x E uses 22 + 0 + 2x1x4 = 30 multiplications

Answer = 30 multiplications

.

Source code of Matrix Chain Multiplication

Time complexity of the Matrix Chain Multiplication

The time complexity of the Matrix Chain Multiplication algorithm, when solved using dynamic programming, is O(n^3).

First, initializing the DP table, which is a 2D array of size n x n, takes O(n²) time. The core of the algorithm involves three nested loops, so combining these operations results in a total time complexity of O(n) * O(n) * O(n) = O(n³).

.

Space complexity of the Matrix Chain Multiplication

The space complexity of the Matrix Chain Multiplication algorithm using dynamic programming is O(n²). This complexity is mainly due to the storage requirements for the dynamic programming table.

.

Applications of Matrix Chain Multiplication Algorithm

1. Computer Graphics – In graphics processing, matrix chain multiplication is used to compute transformations of objects and scenes efficiently, which involves multiple matrix multiplications.
2. Optimization Problems – The algorithm is used in various optimization problems where multiple operations are performed on matrices, such as in network design and resource allocation.
3. Scientific Computations – It is applied in scientific and engineering fields where large-scale matrix operations are common, such as simulations and modelling in physics and engineering.
4. Machine Learning – In machine learning and data science, matrix chain multiplication can be used for optimizing algorithms that involve multiple matrix operations, such as in neural network training and data processing.