Introduction to Kruskal’s Algorithm
- Kruskal’s Algorithm is a fundamental method in the field of graph theory and network optimization.
- Developed by Joseph Kruskal, this algorithm is employed to find the Minimum Spanning Tree (MST) of a connected, undirected graph.
- The primary objective of the algorithm is to discover the smallest set of edges that connects all the vertices in the graph without forming any cycles.
.
Definition of Kruskal’s Algorithm
Kruskal’s Algorithm is a greedy algorithm used to find the Minimum Spanning Tree (MST) of a connected, undirected graph.
The primary objective of the algorithm is to discover the smallest set of edges that connects all the vertices in the graph without forming any cycles.
.
Algorithm of Kruskal(Graph G)
Sort edges of G in non-descending order by weight
Initialize an empty MST and set of trees (forest).
for each edge in G:
if adding edge to T does not form a cycle:
Add edge to T
Merge the trees
return T
.
Working of Kruskal’s Algorithm
- Sort Edges – Begin by sorting all the edges in non-decreasing order based on their weights.
- Initialize Forest – Create a forest (a collection of trees), where each vertex is initially a separate tree.
- Iterate Through Edges – Starting with the smallest edge, check if adding it to the forest forms a cycle. If not, include it in the MST.
- Union Operation – If the edge is added, perform a union operation to merge the two trees into one.
- Repeat – Repeat steps 3 and 4 until all vertices are part of a single tree.
.
Imagine you have a network of houses, and you want to build roads between them with the least total distance.

We can simplify this by arranging the alphabets in place of houses.
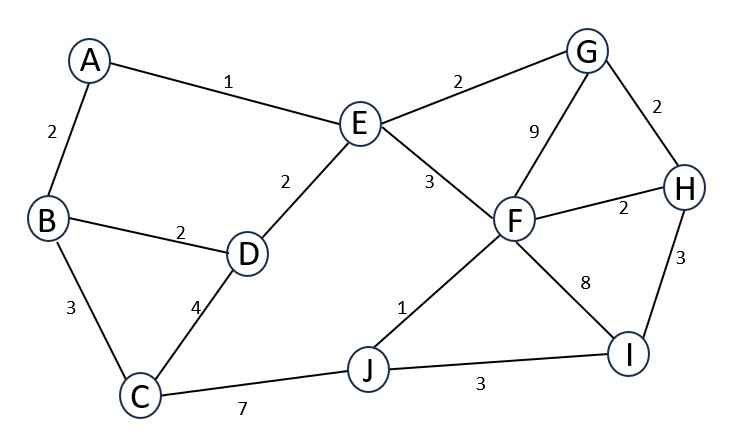
.
Sort Edges
We have to sort the edges to apply kruskal’s theorem. In this graph there are 16 edges.
Edge Structure– (starting vertex, stopping vertex, weight)
The sorted edges are

.
Iterate through Edges
Step 1 – In the sorted edges, first edge AE and its weight is 1. Adding it to the MST does not forms a cycle.
Add AE to MST.
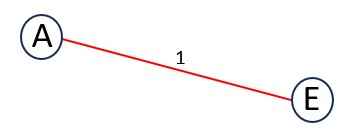
.
Step 2 – Next Edge is FJ and its weight is 1.
Adding it to the MST does not forms a cycle.
Add FJ to MST.
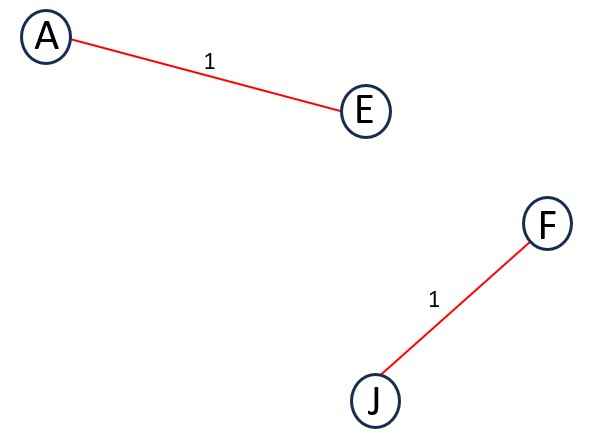
.
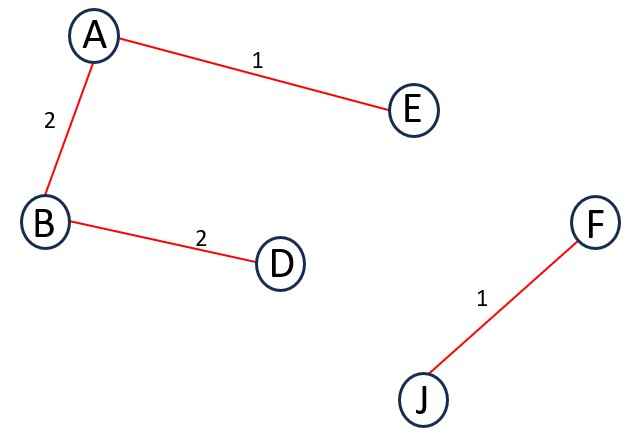
Step 3 – Next Edge is AB and its weight is 2.
Adding it to the MST does not forms a cycle.
Add AB to MST.
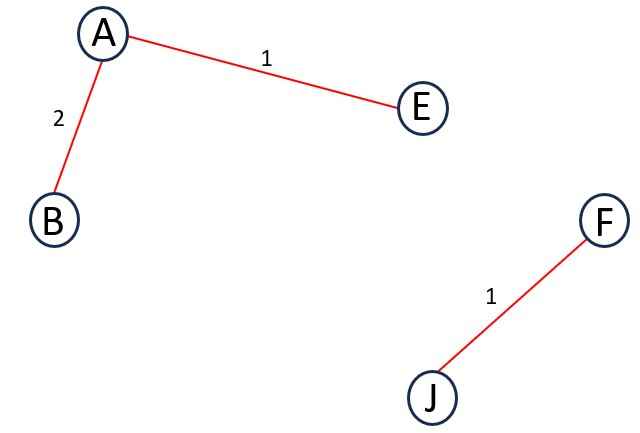
Step 4 – Next Edge is BD and its weight is 2.
Adding it to the MST does not forms a cycle.
Add BD to MST.
Step 5 – Next Edge is DE and its weight is 2.
Adding it to the MST forms a cycle. So, do not add DE to MST.
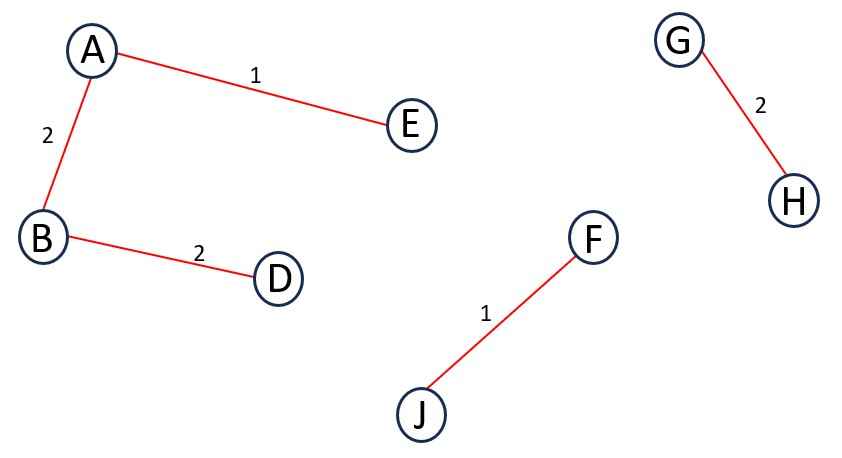
Step 6 – Next Edge is GH and its weight is 2.
Adding it to the MST does not forms a cycle.
Add GH to MST.
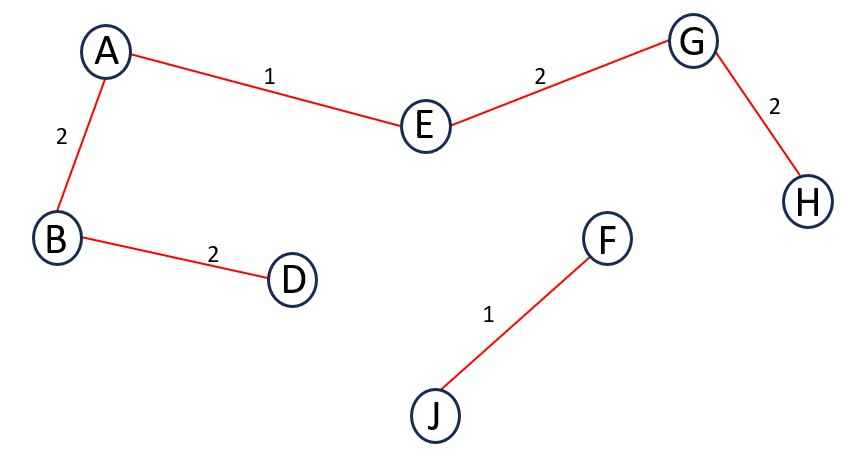
Step 7 – Next Edge is EG and its weight is 2.
Adding it to the MST does not forms a cycle.
Add EG to MST.
.
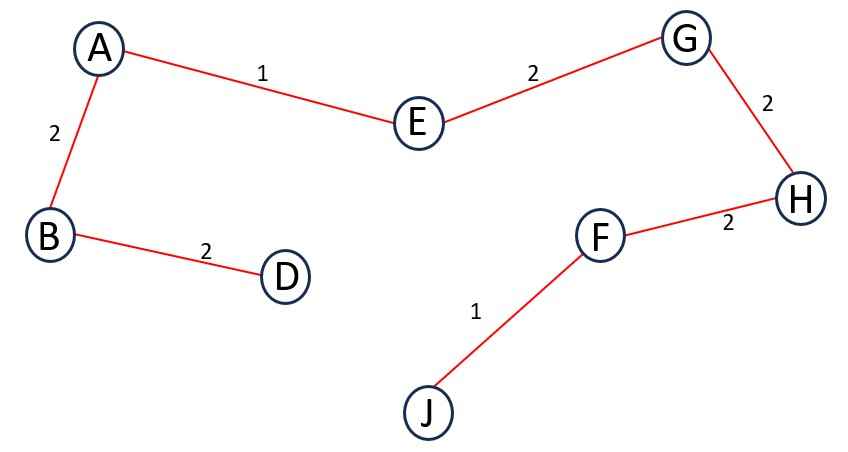
Step 8 – Next Edge is HF and its weight is 2.
Adding it to the MST does not forms a cycle.
Add HF to MST.
.
Step 9 – Next Edge is BC and its weight is 3.
Adding it to the MST does not forms a cycle.
Add BC to MST.
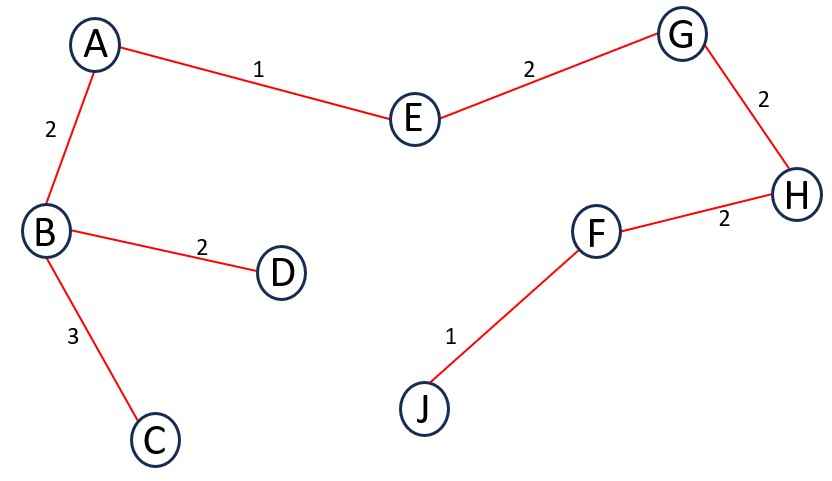
Step 10 – Next Edge is EF and its weight is 3.
Adding it to the MST forms a cycle. So, do not add EF to MST.
Step 11 – Next Edge is HI and its weight is 3.
Adding it to the MST does not forms a cycle.
Add HI to MST.

.
Step 12 – In this step, we found that all the vertices which are in graph has been discovered by us. So, no new operation is needed.
- All the vertices are connected in a single tree.
- There is no new forest of vertices (disconnected vertices).
- The edges weight is 1 + 1 + 2 + 2 + 2 + 2 + 2 + 3 + 3 = 18 that is the minimum spanning tree.
.
Source Code of Kruskal’s Algorithm
// COMPUTER GEEK – compgeek.co.in
// Write a program for Kruskal’s Algorithm
#include <stdio.h>
#include <stdlib.h>
// Structure to represent an edge in the graph
struct Edge
{
int src, dest, weight;
};
// Structure to represent a subset for union-find
struct Subset
{
int parent;
int rank;
};
// Functions
int find(struct Subset subsets[], int i);
void Union(struct Subset subsets[], int x, int y);
void KruskalMST(struct Edge edges[], int V, int E);
int main()
{
int V, E;
// Input the number of vertices and edges
printf(“Enter the number of vertices: “);
scanf(“%d”, &V);
printf(“Enter the number of edges: “);
scanf(“%d”, &E);
// Input the edges with weights
struct Edge* edges = (struct Edge*)malloc(E * sizeof(struct Edge));
for (int i = 0; i < E; ++i)
{
printf(“Enter edge %d (source, destination, weight): “, i + 1);
scanf(“%d %d %d”, &edges[i].src, &edges[i].dest, &edges[i].weight);
}
// Find the MST using Kruskal’s algorithm
KruskalMST(edges, V, E);
free(edges);
return 0;
}
// Find set of an element i
int find(struct Subset subsets[], int i)
{
if (subsets[i].parent != i)
subsets[i].parent = find(subsets, subsets[i].parent);
return subsets[i].parent;
}
// Union of two sets x and y
void Union(struct Subset subsets[], int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
// Attach smaller rank tree under root of high rank tree
if (subsets[xroot].rank < subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank > subsets[yroot].rank)
subsets[yroot].parent = xroot;
else {
// If ranks are the same, make one as root and increment its rank
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
// Compare function for sorting edges by weight in non-descending order
int compare(const void* a, const void* b) {
return ((struct Edge*)a)->weight – ((struct Edge*)b)->weight;
}
// Kruskal’s algorithm to find the Minimum Spanning Tree (MST)
void KruskalMST(struct Edge edges[], int V, int E) {
// Sort the edges in non-descending order by weight
qsort(edges, E, sizeof(edges[0]), compare);
// Allocate memory for subsets
struct Subset* subsets = (struct Subset*)malloc(V * sizeof(struct Subset));
// Initialize subsets for each vertex
for (int i = 0; i < V; ++i) {
subsets[i].parent = i;
subsets[i].rank = 0;
}
// Initialize result (MST) and index for the result array
struct Edge* result = (struct Edge*)malloc((V – 1) * sizeof(struct Edge));
int e = 0; // Index for the result array
// Iterate through all sorted edges
for (int i = 0; e < V – 1 && i < E; ++i) {
// Find the sets of the source and destination vertices
int x = find(subsets, edges[i].src);
int y = find(subsets, edges[i].dest);
// If including this edge doesn’t form a cycle, add it to the result
if (x != y) {
result[e++] = edges[i];
Union(subsets, x, y);
}
}
// Print the MST
printf(“Minimum Spanning Tree (MST) formed by Kruskal’s algorithm:\n”);
for (int i = 0; i < V – 1; ++i) {
printf(“Edge %d: %d — %d Weight: %d\n”, i + 1, result[i].src, result[i].dest, result[i].weight);
}
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Kruskal’s Algorithm
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// Structure to represent an edge in the graph
struct Edge
{
int src, dest, weight;
};
// Structure to represent a subset for union-find
struct Subset
{
int parent;
int rank;
};
// Function prototypes
int find(vector<Subset>& subsets, int i);
void Union(vector<Subset>& subsets, int x, int y);
void KruskalMST(vector<Edge>& edges, int V, int E);
int main()
{
int V, E;
// Input the number of vertices and edges
cout << “Enter the number of vertices: “;
cin >> V;
cout << “Enter the number of edges: “;
cin >> E;
// Input the edges with weights
vector<Edge> edges(E);
for (int i = 0; i < E; ++i) {
cout << “Enter edge ” << i + 1 << ” (source, destination, weight): “;
cin >> edges[i].src >> edges[i].dest >> edges[i].weight;
}
// Find the MST using Kruskal’s algorithm
KruskalMST(edges, V, E);
return 0;
}
// Find set of an element i
int find(vector<Subset>& subsets, int i)
{
if (subsets[i].parent != i)
subsets[i].parent = find(subsets, subsets[i].parent);
return subsets[i].parent;
}
// Union of two sets x and y
void Union(vector<Subset>& subsets, int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
// Attach smaller rank tree under root of high rank tree
if (subsets[xroot].rank < subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank > subsets[yroot].rank)
subsets[yroot].parent = xroot;
else
{
// If ranks are the same, make one as root and increment its rank
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
// Compare function for sorting edges by weight in non-descending order
bool compare(const Edge& a, const Edge& b)
{
return a.weight < b.weight;
}
// Kruskal’s algorithm to find the Minimum Spanning Tree (MST)
void KruskalMST(vector<Edge>& edges, int V, int E)
{
// Sort the edges in non-descending order by weight
sort(edges.begin(), edges.end(), compare);
// Allocate memory for subsets
vector<Subset> subsets(V);
// Initialize subsets for each vertex
for (int i = 0; i < V; ++i)
{
subsets[i].parent = i;
subsets[i].rank = 0;
}
// Initialize result (MST) and index for the result array
vector<Edge> result;
result.reserve(V – 1);
int e = 0; // Index for the result array
// Iterate through all sorted edges
for (int i = 0; e < V – 1 && i < E; ++i)
{
// Find the sets of the source and destination vertices
int x = find(subsets, edges[i].src);
int y = find(subsets, edges[i].dest);
// If including this edge doesn’t form a cycle, add it to the result
if (x != y)
{
result.push_back(edges[i]);
Union(subsets, x, y);
++e;
}
}
// Print the MST
cout << “Minimum Spanning Tree (MST) formed by Kruskal’s algorithm:\n”;
for (int i = 0; i < V – 1; ++i)
{
cout << “Edge ” << i + 1 << “: ” << result[i].src << ” — ” << result[i].dest << ” Weight: ” << result[i].weight << “\n”;
}
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Kruskal’s Algorithm
import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;
class KruskalAlgorithm
{
// Structure to represent an edge in the graph
static class Edge
{
int src, dest, weight;
Edge(int src, int dest, int weight)
{
this.src = src;
this.dest = dest;
this.weight = weight;
}
}
// Structure to represent a subset for union-find
static class Subset
{
int parent;
int rank;
}
// Function to find set of an element i
static int find(Subset[] subsets, int i)
{
if (subsets[i].parent != i)
subsets[i].parent = find(subsets, subsets[i].parent);
return subsets[i].parent;
}
// Function to perform union of two sets x and y
static void union(Subset[] subsets, int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
// Attach smaller rank tree under root of high rank tree
if (subsets[xroot].rank < subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank > subsets[yroot].rank)
subsets[yroot].parent = xroot;
else
{
// If ranks are the same, make one as root and increment its rank
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
// Function to compare edges by weight for sorting
static class EdgeComparator implements Comparator<Edge>
{
@Override
public int compare(Edge a, Edge b)
{
return Integer.compare(a.weight, b.weight);
}
}
// Function to find the Minimum Spanning Tree (MST) using Kruskal’s algorithm
static void kruskalMST(Edge[] edges, int V, int E)
{
// Sort the edges in non-descending order by weight
Arrays.sort(edges, new EdgeComparator());
// Initialize subsets for each vertex
Subset[] subsets = new Subset[V];
for (int i = 0; i < V; ++i)
{
subsets[i] = new Subset();
subsets[i].parent = i;
subsets[i].rank = 0;
}
// Initialize result (MST) and index for the result array
Edge[] result = new Edge[V – 1];
int e = 0; // Index for the result array
// Iterate through all sorted edges
for (int i = 0; e < V – 1 && i < E; ++i)
{
// Find the sets of the source and destination vertices
int x = find(subsets, edges[i].src);
int y = find(subsets, edges[i].dest);
// If including this edge doesn’t form a cycle, add it to the result
if (x != y)
{
result[e++] = edges[i];
union(subsets, x, y);
}
}
// Print the MST
System.out.println(“Minimum Spanning Tree (MST) formed by Kruskal’s algorithm:”);
for (int i = 0; i < V – 1; ++i)
{
System.out.println(“Edge ” + (i + 1) + “: ” + result[i].src + ” — ” + result[i].dest + ” Weight: ” + result[i].weight);
}
}
public static void main(String[] args)
{
Scanner scanner = new Scanner(System.in);
// Input the number of vertices and edges
System.out.print(“Enter the number of vertices: “);
int V = scanner.nextInt();
System.out.print(“Enter the number of edges: “);
int E = scanner.nextInt();
// Input the edges with weights
Edge[] edges = new Edge[E];
for (int i = 0; i < E; ++i)
{
System.out.print(“Enter edge ” + (i + 1) + ” (source, destination, weight): “);
edges[i] = new Edge(scanner.nextInt(), scanner.nextInt(), scanner.nextInt());
}
// Find the MST using Kruskal’s algorithm
kruskalMST(edges, V, E);
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for Kruskal’s Algorithm
class Subset:
def __init__(self, parent, rank):
self.parent = parent
self.rank = rank
class Edge:
def __init__(self, src, dest, weight):
self.src = src
self.dest = dest
self.weight = weight
def find(subsets, i):
if subsets[i].parent != i:
subsets[i].parent = find(subsets, subsets[i].parent)
return subsets[i].parent
def union(subsets, x, y):
xroot = find(subsets, x)
yroot = find(subsets, y)
if subsets[xroot].rank < subsets[yroot].rank:
subsets[xroot].parent = yroot
elif subsets[xroot].rank > subsets[yroot].rank:
subsets[yroot].parent = xroot
else:
subsets[yroot].parent = xroot
subsets[xroot].rank += 1
def kruskal_mst(edges, V, E):
edges.sort(key=lambda edge: edge.weight)
subsets = [Subset(i, 0) for i in range(V)]
result = []
e = 0
i = 0
while e < V – 1 and i < E:
x = find(subsets, edges[i].src)
y = find(subsets, edges[i].dest)
if x != y:
result.append(edges[i])
union(subsets, x, y)
e += 1
i += 1
print(“Minimum Spanning Tree (MST) formed by Kruskal’s algorithm:”)
for i, edge in enumerate(result):
print(f”Edge {i + 1}: {edge.src} — {edge.dest} Weight: {edge.weight}”)
def main():
V = int(input(“Enter the number of vertices: “))
E = int(input(“Enter the number of edges: “))
edges = []
for i in range(E):
print(f”Enter edge {i + 1} (source, destination, weight): “, end=””)
src, dest, weight = map(int, input().split())
edges.append(Edge(src, dest, weight))
kruskal_mst(edges, V, E)
if __name__ == “__main__”:
main()
Sparse Graphs
Definition – Sparse graphs are graphs where the number of edges is much smaller compared to the maximum possible edges between the vertices.
In other words, there are relatively few existing connections among the vertices.
.
Kruskal’s Algorithm in Sparse Graphs
Edge-Focused Approach
Kruskal’s algorithm primarily focuses on sorting edges based on their weights and adding them to the Minimum Spanning Tree (MST) as long as they do not form cycles.
In sparse graphs, where there are fewer existing edges, the edge-focused approach of Kruskal’s algorithm becomes advantageous.
.
Efficiency in Sparse Connectivity
As sparse graphs have a limited number of existing connections, the sorting and processing of edges become more efficient.
.
Comparison with Dense Graphs
In dense graphs, where the number of edges is closer to the maximum possible (nearly complete graphs), Kruskal’s algorithm might become less efficient. This is due to the sorting step becoming more time-consuming as the number of edges increases.
.
Time Complexity of Kruskal’s Algorithm
- Time to sort the edges = O(E log E)
- In Union find operation in worst case is equal to O(log V), where V is the number of vertices.
- The dominant factor in the time complexity is usually the sorting step, so the overall time complexity is often expressed as O(E log E).
.
Space Complexity of Kruskal’s Algorithm
The overall space complexity of Kruskal’s algorithm can be expressed as O(E + V), where E is the number of edges, and V is the number of vertices.
.
Application of Kruskal’s Algorithm
- In the design of computer networks or telecommunication networks, Kruskal’s algorithm can be used to find the minimum cost infrastructure that connects all the nodes.
- Kruskal’s algorithm can be used in transportation planning to find the minimum cost road or railway network that connects different regions or cities.
- Kruskal’s algorithm can be used in image processing for segmenting images into regions with similar characteristics while minimizing the total cost of segmentation.
- In bioinformatics, Kruskal’s algorithm can be used to analyze the evolutionary relationships between different species based on genetic data.
- Kruskal’s algorithm can be used in data analysis to find the hierarchy of clusters in a dataset, where the goal is to group similar data points together.
Test Yourself
Q1- Explain the key difference between Kruskal’s algorithm and Prim’s algorithm for finding minimum spanning trees.
Kruskal’s algorithm is based on sorting edges by weight and adding them to the MST as long as no cycles are formed. It will create a forest of trees or disjoint set of trees.
Prim’s algorithm grows the MST from an initial vertex by adding the lightest edge connecting the growing MST to an external vertex.
Q2- Can Kruskal’s algorithm handle graphs with negative-weight edges? Explain why or why not.
No, Kruskal’s algorithm cannot handle graphs with negative-weight edges. It relies on the greedy approach, and negative edges can create a situation, where adding an edge later might be more beneficial, leading to an incorrect result.
Q3- Discuss a scenario where Kruskal’s algorithm might be more suitable than Prim’s algorithm.
Kruskal’s algorithm and Prim’s algorithm are both used to find the Minimum Spanning Tree (MST) in a graph, but they approach the problem in different ways.
Consider a scenario where you are tasked with designing a communication network for a city with numerous buildings, and the network needs to connect different buildings with minimal cost. The graph representing the city’s layout is sparse, meaning there are relatively few direct connections between buildings compared to the total number of buildings.
Kruskal’s algorithm operates on edges rather than vertices. In a sparse graph, where there are many buildings but relatively few direct connections, Kruskal’s algorithm can be more efficient.
Prim’s algorithm, on the other hand, is more focused on vertices and tends to perform well in dense graphs. In a sparse graph scenario, where there are fewer existing connections, the edge-based approach of Kruskal’s algorithm can lead to a more efficient solution.
Q4- How does Kruskal’s algorithm ensure that it does not form cycles in the process of building the Minimum Spanning Tree (MST)?
Kruskal’s algorithm uses the Union-Find data structure to keep track of disjoint sets. This data structure provides two essential operations:
Find (or Find-Set)
Given an element, this operation identifies the representative (root) of the set to which the element belongs.
Union
Merges two sets into a single set.
Before adding an edge to the MST, it checks if the source and destination vertices belong to the same set. If they do, adding the edge would create a cycle, so the edge is skipped.
Q5- Under what circumstances can Kruskal’s algorithm be less efficient than Prim’s algorithm?
Kruskal’s algorithm can be less efficient when the graph is dense (many edges), as the sorting step becomes more time-consuming. In such cases, Prim’s algorithm, which focuses on vertices, might perform better.
Q6- Discuss the impact of edge weights on the performance of Kruskal’s algorithm.
If all weights are distinct, the MST is unique.
If weights are not distinct, multiple MSTs may exist. In case of equal weights, Kruskal’s algorithm may choose different edges, leading to different MSTs.
So, if edge weights are distinct, sorting them can be done efficiently, resulting in a straightforward implementation with a time complexity of O(E log E).
Q7- In what type of graph would Kruskal’s algorithm have the same time complexity as Prim’s algorithm?
Kruskal’s algorithm has the same time complexity as Prim’s algorithm in a dense graph with a large number of vertices, where the sorting step dominates the overall complexity.
Q8- What is the time complexity of Kruskal’s algorithm in terms of sorting edges?
1. O(E log V)
2. O(V log E)
3. O(E log E)
4. O(V^2)
Ans – (3)
Explanation –
The dominant factor is the sorting step, which takes O(E log E) time.
Q9- In Kruskal’s algorithm, when is an edge added to the MST?
1. If it has the maximum weight and does not form a cycle.
2. If it has the minimum weight and does not form a cycle.
3. If it connects the most vertices
4. If it forms a cycle
Ans – (2)
Explanation – Kruskal’s algorithm adds edges to the MST in non-decreasing order of weight.
Q10- What is the primary drawback of Kruskal’s algorithm in terms of space complexity?
1. Requires a large amount of memory
2. Requires a dynamic data structure
3. Requires extra storage for subsets
4. Requires a priority queue
Ans – (3)
Explanation – Extra storage is needed for the Union-Find data structure.
Q11- Kruskal’s algorithm can be less efficient than Prim’s algorithm in a dense graph. (True/False)
Ans – (True)
Explanation – Kruskal’s algorithm can be less efficient in a dense graph due to the sorting step.
Q12- In Kruskal’s algorithm, what is checked before adding an edge to the MST?
1. Edge weight
2. Source vertex
3. Destination vertex
4. Formation of a cycle
Ans – (4)
Explanation – The algorithm checks if adding the edge would create a cycle in the MST.






