Today, we’re going to explore the “Jump Search” algorithm, a powerful technique used in the field of Design and Analysis of Algorithms. Don’t worry if you’re new to this, we’ll break it down in simple terms.
.
Introduction
Jump Search is like a treasure hunt. Imagine you’re searching for a specific item in a large pile, but instead of checking every item one by one, you take giant leaps and narrow down your search. It’s an efficient way to find what you’re looking for, and that’s what Jump Search does with data.
Jump search was invented by William Kellogg and Kenneth Patz in 2002.
.
What is a Jump Search
- Jump Search is a searching algorithm used to locate a specific element within a sorted array or list by making a series of jumps or steps, which allows for a more efficient search process.
- If array is sorted, then we can search the target element first at b location, then 2b location and then 3b, 4b… up to the array ends.
- At any moment, if target element is larger than the array element, then search at most b more elements in gap.
- Time Complexity: n/b + b where n is numbers in array.
- This process continues until the target element is found or it is determined that the element does not exist in the array.
How b is calculated?
If n = 100
b | n/b + b
-------------
2 | 52
5 | 25
10 | 20 (min)
15 | 22
20 | 25
50 | 52
So, in b = 10, there is the smallest comparison in the jump search, it means for n = 100, b = √n = 10
There is another method to find b which gives correct result.
To find smallest b, we can differentiate (n/b + n) with respect to b.
Differentiate (n/b + b) = 0
-> d/db (n/b + b) = 0
-> -n/b2 + 1 = 0
-> b2 = n
-> b = √n
Number of operations when b = √n
So, (n/b + b) = (n/√n + √n) = 2√n
It means, Ɵ(√n) is time complexity.
.
How Jump Search Works
Sorting– First, your data must be sorted in ascending order. This is essential for Jump Search to work effectively.
Setting the Jump– Determine a “jump size” or “step.” This step defines how far you’ll leap through the data while searching. A common choice is the square root of the data size.
Jumping– Start with the first element and jump ahead in fixed steps. If the array element is greater than the target element, then backtrack (last element which is less than the target element) and perform a linear search.
Repeat Until Found– Keep jumping and searching until you find the desired element or determine that it’s not in the data.
.
The Jump Search Algorithm
1. Let 'array' be the sorted array to search.
2. Let 'n' be the size of the array.
3. Let 'step' be the jump size (often sqrt(n)).
4. Initialize 'prev' to 0.
5. While 'array[min(step, n) - 1]' < 'target':
- Set 'prev' to 'step'.
- Increment 'step' by 'sqrt(n)'.
- If 'prev' >= 'n'
the target is not in the array; stop.
6. Perform a linear search in the range 'prev'
to 'min(step, n)' for the 'target'.
7. If found, return the index;
otherwise, return -1 (not found).
.
Example
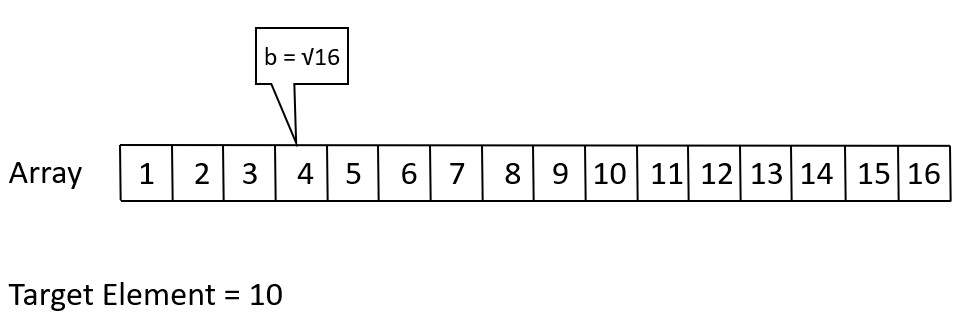
Let’s say you have a sorted array
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16],
and you want to find the number 10.
The jump size would be sqrt(16) = 4.
.
Start at index 4, (4 < 10), Comparison = 1
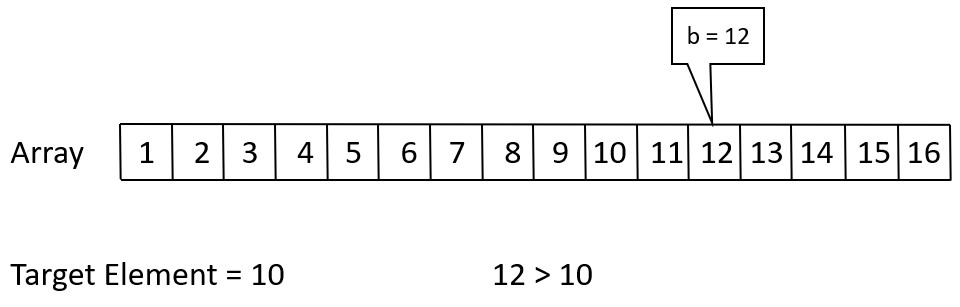
So, jump to value 8. (8 < 10), Comparison = 2

.
So, jump to value 12. (12 > 10), Comparison = 3
.
Since 12 is greater than 10, you backtrack to value 8 and perform a linear search.
You find value 9. (9 < 10), Comparison = 4

.
So, count +1 for 9, the value is 10 (10 = 10). Comparison = 5
Search successful.

Source Code of Jump Search
// COMPUTER GEEK – compgeek.co.in
// Write a program for Jump Search Algorithm
#include <stdio.h>
#include <math.h>
// Function to choose minimum
int min(int a, int b) {
return (a < b) ? a : b;
}
// Function to perform Jump Search
int jumpSearch(int arr[], int n, int target)
{
int step = (int)sqrt(n); // Calculate the jump step size
int prev = 0; // Initialize the previous index
while (arr[min(step, n) – 1] < target)
{
// Jumping forward while the value at the current step is less than the target
prev = step;
step += (int)sqrt(n);
// If the current step exceeds the array size, break out of the loop
if (prev >= n)
return -1;
}
// Perform a linear search within the block
while (arr[prev] < target)
{
prev++;
// If we’ve reached the next block or the end of the array, the target is not in the array
if (prev == min(step, n))
return -1;
}
// If the target element is found, return its index
if (arr[prev] == target)
return prev;
return -1; // If the target element is not in the array, return -1
}
int main()
{
int n;
printf(“Enter the number of elements in the array: “);
scanf(“%d”, &n);
int arr[n];
printf(“Enter the sorted array elements:\n”);
for (int i = 0; i < n; i++)
{
scanf(“%d”, &arr[i]);
}
int target;
printf(“Enter the target element to search for: “);
scanf(“%d”, &target);
int result = jumpSearch(arr, n, target);
if (result != -1)
printf(“Element %d found at index %d\n”, target, result);
else
printf(“Element %d not found in the array\n”, target);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Jump Search Algorithm
#include <iostream>
#include <cmath>
using namespace std;
// Function to choose minimum
int min(int a, int b) {
return (a < b) ? a : b;
}
// Function to perform Jump Search
int jumpSearch(int arr[], int n, int target) {
int step = (int)sqrt(n); // Calculate the jump step size
int prev = 0; // Initialize the previous index
while (arr[min(step, n) – 1] < target) {
// Jumping forward while the value at the current step is less than the target
prev = step;
step += (int)sqrt(n);
// If the current step exceeds the array size, break out of the loop
if (prev >= n)
return -1;
}
// Perform a linear search within the block
while (arr[prev] < target) {
prev++;
// If we’ve reached the next block or the end of the array, the target is not in the array
if (prev == min(step, n))
return -1;
}
// If the target element is found, return its index
if (arr[prev] == target)
return prev;
return -1; // If the target element is not in the array, return -1
}
int main() {
int n;
cout << “Enter the number of elements in the array: “;
cin >> n;
int arr[n];
cout << “Enter the sorted array elements:” << endl;
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
int target;
cout << “Enter the target element to search for: “;
cin >> target;
int result = jumpSearch(arr, n, target);
if (result != -1)
cout << “Element ” << target << ” found at index ” << result << endl;
else
cout << “Element ” << target << ” not found in the array” << endl;
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Jump Search Algorithm
import java.util.Scanner;
public class JumpSearch
{
// Function to choose the minimum of two numbers
static int min(int a, int b)
{
return (a < b) ? a : b;
}
// Function to perform Jump Search
static int jumpSearch(int[] arr, int target)
{
int n = arr.length;
int step = (int) Math.sqrt(n); // Calculate the jump step size
int prev = 0; // Initialize the previous index
while (arr[min(step, n) – 1] < target)
{
// Jumping forward while the value at the current step is less than the target
prev = step;
step += (int) Math.sqrt(n);
// If the current step exceeds the array size, break out of the loop
if (prev >= n)
return -1;
}
// Perform a linear search within the block
while (arr[prev] < target)
{
prev++;
// If we’ve reached the next block or the end of the array, the target is not in the array
if (prev == min(step, n))
return -1;
}
// If the target element is found, return its index
if (arr[prev] == target)
return prev;
return -1; // If the target element is not in the array, return -1
}
public static void main(String[] args)
{
Scanner scanner = new Scanner(System.in);
System.out.print(“Enter the number of elements in the array: “);
int n = scanner.nextInt();
int[] arr = new int[n];
System.out.println(“Enter the sorted array elements:”);
for (int i = 0; i < n; i++)
{
arr[i] = scanner.nextInt();
}
System.out.print(“Enter the target element to search for: “);
int target = scanner.nextInt();
int result = jumpSearch(arr, target);
if (result != -1)
System.out.printf(“Element %d found at index %d\n”, target, result);
else
System.out.printf(“Element %d not found in the array\n”, target);
scanner.close();
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for Jump Search Algorithm
import math
# Function to choose minimum
def min(a, b):
return a if a < b else b
# Function to perform Jump Search
def jump_search(arr, target):
n = len(arr)
step = int(math.sqrt(n)) # Calculate the jump step size
prev = 0 # Initialize the previous index
while arr[min(step, n) – 1] < target:
# Jumping forward while the value at the current step is less than the target
prev = step
step += int(math.sqrt(n))
# If the current step exceeds the array size, break out of the loop
if prev >= n:
return -1
# Perform a linear search within the block
while arr[prev] < target:
prev += 1
# If we’ve reached the next block or the end of the array, the target is not in the array
if prev == min(step, n):
return -1
# If the target element is found, return its index
if arr[prev] == target:
return prev
return -1 # If the target element is not in the array, return -1
# Input the sorted array elements as space-separated values
arr = list(map(int, input(“Enter the sorted array elements separated by spaces: “).split()))
target = int(input(“Enter the target element to search for: “))
result = jump_search(arr, target)
if result != -1:
print(f”Element {target} found at index {result}”)
else:
print(f”Element {target} not found in the array”)
Time and Space Complexity
- Best case Jump Search performs at most 1 comparison because target element = square root of n.
- Average and Worst-case Jump search performs O(√n) comparison.
- Space Complexity– O(1) – Jump Search uses a constant amount of extra space for variables, regardless of the input size.
Advantages of Jump Search
- Efficient for searching in sorted arrays.
- Requires less time compared to linear search, especially for large datasets.
- It’s simple to implement.
Disadvantages of Jump Search
- Requires sorted data, which can be a limitation.
- May perform poorly for datasets with many repeated values.
- It’s not suitable for unsorted data.
Applications of Jump Search
- Searching in databases and indexing systems.
- File systems for quick file retrieval.
- Wherever a sorted dataset needs efficient search operations.
Test Yourself
Q1- Explain the concept of Jump Search in algorithms.
Jump Search is a searching algorithm used to locate a specific element within a sorted array or list by making a series of jumps or steps, allowing for an efficient search process. It works by dividing the data into blocks and performing a jump to narrow down the search.
Q2- What is the significance of sorting data before using the Jump Search algorithm?
Sorting the data is essential for Jump Search because it relies on the data being in ascending order. Without sorting, Jump Search cannot efficiently locate the target element.
Q3- How is the “jump size” or “step” determined in the Jump Search algorithm?
The jump size, often denoted as ‘b,’ is typically set to the square root of the size of the data (sqrt(n)).
It defines how far you jump through the data while searching.
Q4- Explain the process of jumping and searching in the Jump Search algorithm.
Jump Search starts with the first element and jumps ahead in fixed steps (determined by the jump size ‘b’).
It compares each element with the target.
If the element is greater than the target, it backtracks and performs a linear search within the block.
Q5- How is the time complexity of Jump Search calculated, and what is it for this algorithm?
We have number of operations (n/b + n)
When b = √n
=> (n/b + b) = (n/√n + √n) = 2√n
=> Ɵ(√n) is time complexity.
Q6- How to find the smallest b?
To find smallest b, we can differentiate (n/b + n) with respect to b.
Differentiate (n/b + b) = 0
-> d/db (n/b + b) = 0
-> -n/b2 + 1 = 0
-> b2 = n
-> b = √n
Q7- What are the advantages of using Jump Search for searching in sorted arrays?
Advantages of Jump Search include efficiency for large datasets, simplicity of implementation, and a time complexity of O(√n) for average and worst cases.
Q8- In the worst-case scenario, how many comparisons are performed in Jump Search for an array of size ‘n’?
In the worst case, Jump Search performs approximately 2√n comparisons for an array of size ‘n.’
Q9- What is the time complexity of the Jump Search algorithm?
O(log n)
O(n)
O(√n)
O(n log n)
Ans – (3)
Explanation – Jump Search has a time complexity of O(√n) for average and worst cases.
Q10- When performing a jump in Jump Search, what does the algorithm do if the array element is greater than the target?
Continues jumping forward
Performs a linear search within the block
Halts the search
Increases the jump size
Ans – (2)
Explanation – It backtracks and performs a linear search when encountering a larger element.
Q11- Is Jump Search always faster than Linear Search for sorted arrays?
Not necessarily.
While Jump Search is generally faster than Linear Search for large sorted arrays due to its O(√n) time complexity, it can actually be slower than Linear Search for very small arrays or when the target element is located near the beginning of the array. In such cases, the overhead of setting up the jump size may make Linear Search more efficient.
Q12- What is the minimum size an array should have for Jump Search to be more efficient than Binary Search?
Jump Search is typically more efficient than Binary Search for very small arrays (e.g., less than 10-20 elements) due to its lower overhead. However, as the array size increases, Binary Search eventually surpasses Jump Search in terms of efficiency.






