Introduction
The Job Sequencing Problem is a classic optimization problem that falls under the category of Greedy Algorithms. It is a problem related to job scheduling and aims to find the most profitable way to execute a set of jobs within a given time frame. In this article, we’ll explore the basics of the Job Sequencing Problem, how it works, its algorithm, and various aspects associated with it.
.
Problem
Given a set of ‘n’ jobs, where each job ‘i’ has a deadline ‘Di‘ by which it must be completed, a profit ‘Pi‘ associated with it if completed on time, and a processing time ‘Ti‘ find a schedule that maximizes the total profit.
.
Working
The schedule should ensure that each job is completed before or at its respective deadline, and the processing times do not overlap.
The Job Sequencing Problem is all about finding the best way to complete a bunch of tasks.
These tasks have a time limit and a reward attached to them.
You want to finish as many as possible within the time limits to get the most rewards.
It’s like a puzzle where you need to figure out the right order to work on these tasks so that you don’t miss any deadlines and collect the maximum rewards.
.
Algorithm of Job Sequencing Problem
- Sort the jobs in non-ascending order of their profits.
- Initialize an array to keep track of time slots and a variable to store the total profit.
- Iterate through the sorted jobs list.
- For each job, find the highest possible time slot that is available (i.e., not yet allocated).
- Allocate the job to the found time slot and update the total profit.
- Continue this process until all jobs are allocated or no more time slots are available.
.
Example
In university exams, there is a question which comes most of the times.
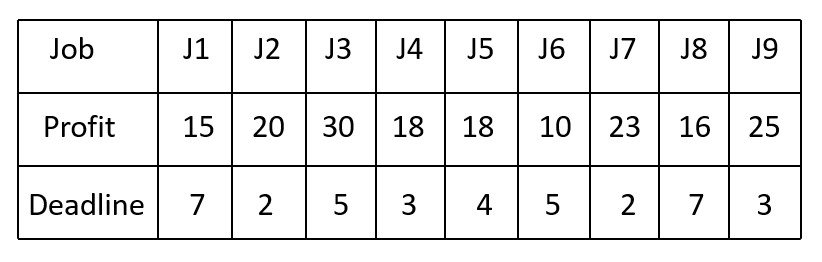
So, we sort the jobs in descending order of their profits.
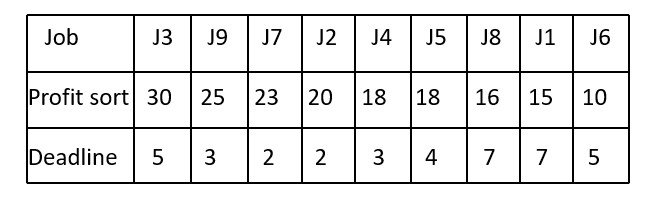
.
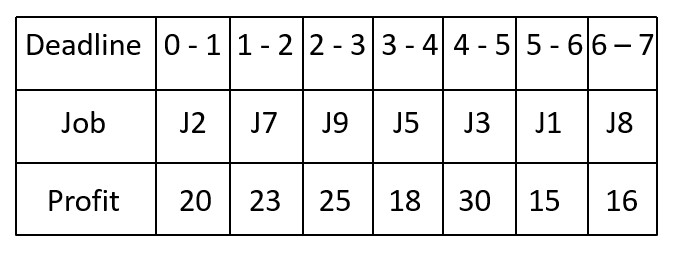
1 First job is J3. (Profit = 30, Deadline = 5)
The highest possible time slot that is available (i.e., not yet allocated) is 4-5.
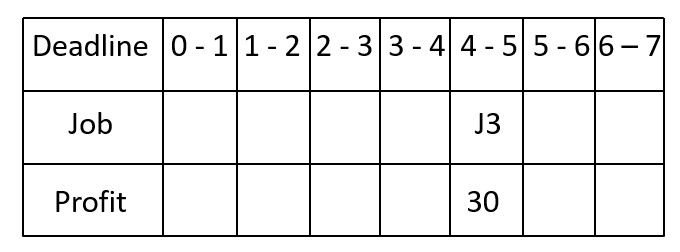
.
2 Next job is J9. (Profit = 25, Deadline = 3)
The highest possible time slot that is available (i.e., not yet allocated) is 2-3.
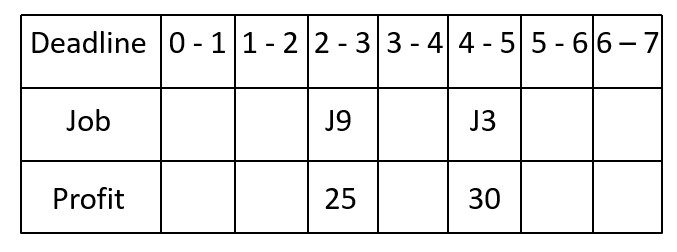
.
3 Next job is J7. (Profit = 23, Deadline = 2)
The highest possible time slot that is available (i.e., not yet allocated) is 1-2.
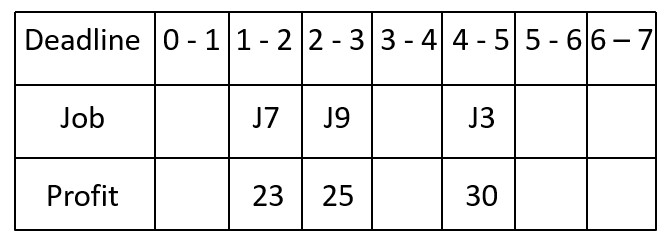
.
4 Next job is J2. (Profit = 20, Deadline = 2)
The highest possible time slot that is available (i.e., not yet allocated) is 0-1, because 1-2 time has been allocated to J7.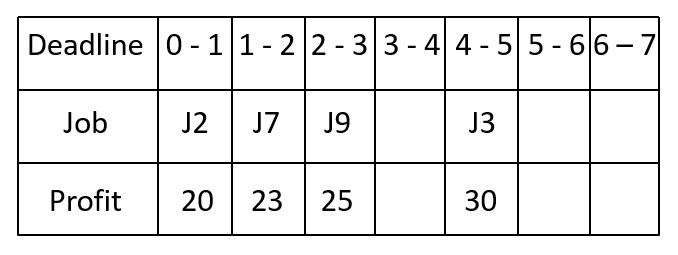
.
5 Next job is J4. (Profit = 18, Deadline = 3)
The highest possible time slot that is available (i.e., not yet allocated) is NONE, because 0-1, 1-2 and 2-3 time has been allocated to J2, J7 and J9, respectively. This job creates an overlap, so skip this.
.
6 Next job is J5. (Profit = 18, Deadline = 4)
The highest possible time slot that is available (i.e., not yet allocated) is 3-4.
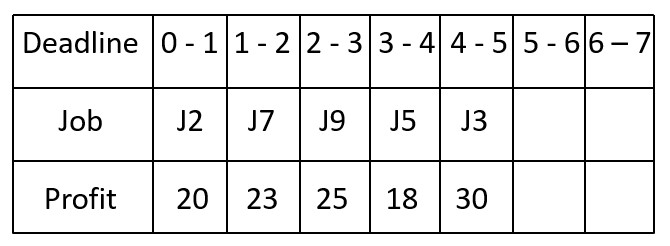
.
7 Next job is J8. (Profit = 16, Deadline = 7)
The highest possible time slot that is available (i.e., not yet allocated) is 6-7.
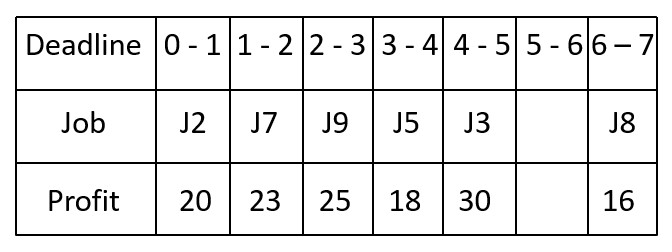
.
8 Next job is J1. (Profit = 15, Deadline = 7)
The highest possible time slot that is available (i.e., not yet allocated) is 5-6, because 6-7 time has been allocated to J8.
.
So, all the slots have been fulfilled. Skip the rest jobs.
The total profit is 20 + 23 + 25 + 18 + 30 + 15 + 16 = 147
.
Source Code for Job Sequencing Problem
// COMPUTER GEEK – compgeek.co.in
// Write a program for Job Sequencing Problem
#include <stdio.h>
#include <stdlib.h>
// Structure to represent a job
struct Job
{
char id;
int profit;
int deadline;
};
// Function to compare jobs based on their profits (in descending order)
int compareJobs(const void *a, const void *b)
{
return ((struct Job *)b)->profit – ((struct Job *)a)->profit;
}
// Function to solve the Job Sequencing Problem
void jobSequencing(struct Job jobs[], int n)
{
// Sort jobs in descending order of profits
qsort(jobs, n, sizeof(struct Job), compareJobs);
// Find the maximum deadline to determine the size of the time slots array
int maxDeadline = 0;
for (int i = 0; i < n; i++)
{
if (jobs[i].deadline > maxDeadline)
{
maxDeadline = jobs[i].deadline;
}
}
// Initialize an array to keep track of time slots and a variable to store the total profit
int *timeSlots = (int *)malloc(maxDeadline * sizeof(int));
int totalProfit = 0;
// Initialize timeSlots array with -1, indicating all slots are initially available
for (int i = 0; i < maxDeadline; i++)
{
timeSlots[i] = -1;
}
// Iterate through the sorted jobs list
for (int i = 0; i < n; i++)
{
// For each job, find the highest possible time slot that is available
for (int j = jobs[i].deadline – 1; j >= 0; j–)
{
if (timeSlots[j] == -1)
{
// Allocate the job to the found time slot and update the total profit
timeSlots[j] = i;
totalProfit += jobs[i].profit;
break;
}
}
}
// Print the job sequence and total profit
printf(“Job Sequence: “);
for (int i = 0; i < maxDeadline; i++)
{
if (timeSlots[i] != -1)
{
printf(“%c “, jobs[timeSlots[i]].id);
}
}
printf(“\nTotal Profit: %d\n”, totalProfit);
free(timeSlots);
}
int main()
{
int n;
printf(“Enter the number of jobs: “);
scanf(“%d”, &n);
struct Job jobs[n];
for (int i = 0; i < n; i++)
{
printf(“Enter details for Job %d (id profit deadline): “, i + 1);
scanf(” %c %d %d”, &jobs[i].id, &jobs[i].profit, &jobs[i].deadline);
}
jobSequencing(jobs, n);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Job Sequencing Problem
#include <iostream>
#include <algorithm>
// Structure to represent a job
struct Job
{
char id;
int profit;
int deadline;
};
// Function to compare jobs based on their profits (in descending order)
bool compareJobs(const Job& a, const Job& b)
{
return a.profit > b.profit;
}
// Function to solve the Job Sequencing Problem
void jobSequencing(Job jobs[], int n)
{
// Sort jobs in descending order of profits
std::sort(jobs, jobs + n, compareJobs);
// Find the maximum deadline to determine the size of the timeSlots array
int maxDeadline = 0;
for (int i = 0; i < n; i++)
{
if (jobs[i].deadline > maxDeadline)
{
maxDeadline = jobs[i].deadline;
}
}
// Initialize an array to keep track of time slots and a variable to store the total profit
int* timeSlots = new int[maxDeadline];
int totalProfit = 0;
// Initialize timeSlots array with -1, indicating all slots are initially available
for (int i = 0; i < maxDeadline; i++)
{
timeSlots[i] = -1;
}
// Iterate through the sorted jobs list
for (int i = 0; i < n; i++)
{
// For each job, find the highest possible time slot that is available
for (int j = std::min(jobs[i].deadline – 1, maxDeadline – 1); j >= 0; j–)
{
if (timeSlots[j] == -1)
{
// Allocate the job to the found time slot and update the total profit
timeSlots[j] = i;
totalProfit += jobs[i].profit;
break;
}
}
}
// Print the job sequence and total profit
std::cout << “Job Sequence: “;
for (int i = 0; i < maxDeadline; i++)
{
if (timeSlots[i] != -1)
{
std::cout << jobs[timeSlots[i]].id << ” “;
}
}
std::cout << “\nTotal Profit: ” << totalProfit << std::endl;
delete[] timeSlots;
}
int main()
{
int n;
std::cout << “Enter the number of jobs: “;
std::cin >> n;
Job jobs[n];
for (int i = 0; i < n; i++)
{
std::cout << “Enter details for Job ” << i + 1 << ” (id profit deadline): “;
std::cin >> jobs[i].id >> jobs[i].profit >> jobs[i].deadline;
}
jobSequencing(jobs, n);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Job Sequencing Problem
import java.util.Arrays;
import java.util.Scanner;
// Class to represent a job
class Job
{
char id;
int profit;
int deadline;
public Job(char id, int profit, int deadline)
{
this.id = id;
this.profit = profit;
this.deadline = deadline;
}
}
class JobSequencing
{
// Function to compare jobs based on their profits (in descending order)
static class JobComparator implements java.util.Comparator<Job>
{
public int compare(Job a, Job b)
{
return b.profit – a.profit;
}
}
// Function to solve the Job Sequencing Problem
static void jobSequencing(Job[] jobs, int n)
{
// Sort jobs in descending order of profits
Arrays.sort(jobs, new JobComparator());
// Find the maximum deadline to determine the size of the timeSlots array
int maxDeadline = 0;
for (int i = 0; i < n; i++)
{
if (jobs[i].deadline > maxDeadline)
{
maxDeadline = jobs[i].deadline;
}
}
// Initialize an array to keep track of time slots and a variable to store the total profit
int[] timeSlots = new int[maxDeadline];
int totalProfit = 0;
// Initialize timeSlots array with -1, indicating all slots are initially available
Arrays.fill(timeSlots, -1);
// Iterate through the sorted jobs list
for (int i = 0; i < n; i++)
{
// For each job, find the highest possible time slot that is available
for (int j = Math.min(jobs[i].deadline – 1, maxDeadline – 1); j >= 0; j–)
{
if (timeSlots[j] == -1)
{
// Allocate the job to the found time slot and update the total profit
timeSlots[j] = i;
totalProfit += jobs[i].profit;
break;
}
}
}
// Print the job sequence and total profit
System.out.print(“Job Sequence: “);
for (int i = 0; i < maxDeadline; i++)
{
if (timeSlots[i] != -1)
{
System.out.print(jobs[timeSlots[i]].id + ” “);
}
}
System.out.println(“\nTotal Profit: ” + totalProfit);
}
public static void main(String[] args)
{
Scanner scanner = new Scanner(System.in);
System.out.print(“Enter the number of jobs: “);
int n = scanner.nextInt();
Job[] jobs = new Job[n];
for (int i = 0; i < n; i++)
{
System.out.print(“Enter details for Job ” + (i + 1) + ” (id profit deadline): “);
char id = scanner.next().charAt(0);
int profit = scanner.nextInt();
int deadline = scanner.nextInt();
jobs[i] = new Job(id, profit, deadline);
}
jobSequencing(jobs, n);
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for Job Sequencing Problem
# Structure to represent a job
class Job:
def __init__(self, id, profit, deadline):
self.id = id
self.profit = profit
self.deadline = deadline
# Function to compare jobs based on their profits (in descending order)
def compare_jobs(job):
return job.profit
# Function to solve the Job Sequencing Problem
def job_sequencing(jobs):
# Sort jobs in descending order of profits
jobs.sort(key=compare_jobs, reverse=True)
# Find the maximum deadline to determine the size of the time_slots list
max_deadline = max(jobs, key=lambda job: job.deadline).deadline
# Initialize a list to keep track of time slots and a variable to store the total profit
time_slots = [-1] * max_deadline
total_profit = 0
# Iterate through the sorted jobs list
for job in jobs:
# For each job, find the highest possible time slot that is available
for j in range(min(job.deadline – 1, max_deadline – 1), -1, -1):
if time_slots[j] == -1:
# Allocate the job to the found time slot and update the total profit
time_slots[j] = job.id
total_profit += job.profit
break
# Print the job sequence and total profit
print(“Job Sequence:”, ” “.join(str(job) for job in time_slots if job != -1))
print(“Total Profit:”, total_profit)
if __name__ == “__main__”:
n = int(input(“Enter the number of jobs: “))
jobs = []
for i in range(n):
job_details = input(f”Enter details for Job {i + 1} (id profit deadline): “).split()
job = Job(job_details[0], int(job_details[1]), int(job_details[2]))
jobs.append(job)
job_sequencing(jobs)
Time complexity of Job Sequencing Problem
- To sort N Jobs – O(nlogn)
- Take each job and start where the deadline is given. Keep searching for the vacant location. So, if there are N jobs for each job, we need to search N slots. i.e O(n2)
So, total time complexity is O(n2).
.
Space Complexity of Job Sequencing Problem
The space complexity is O(n) as it primarily involves storing the jobs and their associated data.
.
Advantages of Job Sequencing Problem
- The greedy algorithm for job sequencing is relatively simple and efficient.
- It provides a quick solution to scheduling problems with the aim of maximizing profits.
- It can be applied to a wide range of practical situations where job scheduling is crucial.
.
Disadvantages of Job Sequencing Problem
- It assumes that the execution times of jobs are the same, which may not hold true in real-world scenarios.
- If not sorted by profit, it might lead to suboptimal solutions.
- It is non-pre-emptive.
- It has a higher average waiting time compared to other algorithms.
- It favours CPU bound processes over I/O bound processes.
- The algorithm assumes that all jobs are independent and can be scheduled without any dependencies or constraints.
- Once a job is skipped due to a missed deadline, it cannot be rescheduled.
.
Applications of Job Sequencing Problem
- Print job scheduling in computer systems.
- In marketing, companies may have multiple advertising campaigns with various deadlines. It can be applied to schedule these campaigns for maximum reach and profitability.
- It can be used in the scheduling of transport vehicles and routes to optimize the delivery of goods, reduce transportation costs, and ensure timely deliveries.
- Educational institutions use this problem to schedule exams to avoid conflicts, reduce idle time between exams, and ensure a fair distribution of exams for students.
- Farmers can use to optimize planting and harvesting schedules, taking into account factors like crop growth cycles and weather conditions.
Test Yourself
Q1- How does the Job Sequencing Problem differ from other scheduling algorithms, such as Round Robin or Shortest Job First (SJF)?
Unlike Round Robin or SJF, the Job Sequencing Problem focuses on job profits and deadlines. It doesn’t consider job durations or prioritize based on time remaining to completion.
Q2- Explain the concept of non-pre-emptive scheduling in the context of the Job Sequencing Problem.
Non-pre-emptive scheduling means once a job is started, it cannot be interrupted or stopped. In the Job Sequencing Problem, it implies that if a job is allocated to a time slot, it must be completed within that time frame.
Q3- 10 jobs are given. The execution of each job takes 1 unit of time. Jobs are given as (Job, Profit, Deadline)
(J1, 25, 4), (J2, 35, 7), (J3, 40, 4), (J4, 30, 7), (J5, 18, 1), (J6, 25, 4), (J7, 33, 6), (J8, 43, 5), (J9, 19, 3), (J10, 25, 6)
The maximum profit earned is ____________ ?
We have to first sort the jobs in non-ascending order of their profits.
(J8, 43, 5), (J3, 40, 4), (J2, 35, 7), (J7, 33, 6), (J4, 30, 7), (J1, 25, 4), (J6, 25, 4), (J10, 25, 6), (J9, 19, 3), (J5, 18, 1).
Total Jobs execute = J8, J3, J2, J7, J4, J1, J6
Maximum Profit = 43 + 40 + 35 + 33 + 30 + 25 + 25 = 231
Q4- Jobs – (J1, J2, J3, J4) Processing Time – (1, 3, 2, 1) Deadline – (3, 3, 2, 4). Maximum jobs can be done is
1
2
3
All
Ans – (3)
Explanation – In this type of problems, we sort the processing time of jobs into non-descending order.
Sorted Jobs – (J1, 1, 3), (J4, 1, 4), (J3, 2, 2), (J2, 3, 3)
Maximum Jobs can be done is 3. (J1, J4, J3)
Q5- You have 8 jobs with their respective profits and deadlines:
(J1, 50, 2), (J2, 35, 3), (J3, 60, 1), (J4, 30, 3), (J5, 45, 5), (J6, 20, 4), (J7, 55, 2), (J8, 40, 4).
What is the maximum profit that can be earned by scheduling these jobs?
To maximize profit, we first sort the jobs in non-ascending order of their profits:
(J3, 60, 1), (J7, 55, 2), (J1, 50, 2), (J5, 45, 5), (J8, 40, 4), (J2, 35, 3), (J4, 30, 3), (J6, 20, 4).
.
Now, let’s schedule the jobs to maximize profit:
Execute J3 within its deadline (Profit = 60).
Execute J7 within its deadline (Profit = 60 + 55 = 115).
Job J1 can’t be executed within its deadline.
Execute J5 within its deadline (Profit = 115 + 45 = 160).
Execute J8 within its deadline (Profit = 160 + 40 = 200).
Execute J2 within its deadline (Profit = 200 + 35 = 235).
Job J4 can’t be executed within its deadline.
Job J6 can’t be executed within its deadline.
.
The maximum profit can be earned is 235.
Q6- 5 jobs are given, and each job takes 2 units of time to complete. The jobs are represented as (Job, Profit, Deadline):
(J1, 15, 2), (J2, 25, 3), (J3, 10, 1), (J4, 20, 3), (J5, 18, 2).
What is the maximum profit that can be earned using the Job Sequencing Problem algorithm?
To maximize the profit, we first need to sort the jobs in non-ascending order of their profits. After sorting, the job sequence becomes:
(J2, 25, 3), (J4, 20, 4), (J5, 18, 5), (J1, 15, 2), (J3, 10, 7).
Each job takes 2 units of time to complete.
Now, we can execute the jobs one by one to maximize the profit. The profit is obtained by executing (J2, J5, J3) is 25 + 18 + 10 = 53.
But, if you see by some other angle, the profit is not maximized. We can do some other jobs with in the timeline.
Executing J2 in the first 2 units of time allows J4 to be executed in the second 2 units of time. After you execute J3. The maximum profit is now to be 25 + 20 + 10 = 55 (which is more than 53).
.
But this is a greedy method and a Greedy algorithm is an approach to solving problems by making locally optimal (best) choices at each step with the hope of finding a global optimum (best) or near-best solution.
The maximum profit is made possible by dynamic programming methodology by which we can create every possible solution to maximize profit.
So, the maximum profit that can be earned in Greedy approach is 53 units.






