Iterative Method

The Second method is the Iterative Method.

The iterative method is excellent because, with this method, you can solve all the recurrence problems. 

Iterative Method:

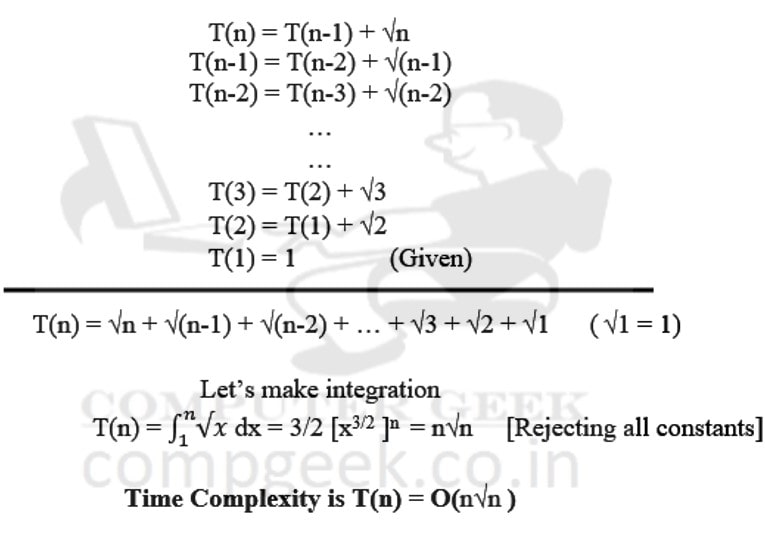
This means that the recurrence is expanded and expressed as a sum of terms from n and the initial condition. T(1) was the required time in the initial state. To transform the recursion, first, decompose T(n) into sub-problem and then sub-sub-problem and then up to T(1).

Solving the Recurrence problem

1. T(n) = T(n – 1) + 1

2. T(n) = T(n – 1) + n

3. T(n) = T(n – 1) + n^2

4. T(n) = T(n – 1) + log n

5. T(n) = 2T(n – 1) + n

6. T(n) = T(n/2) + n

7. T(n) = 2T(n/2) + 1

8. T(n) = 2T(n/2) + n

9. T(n) = T(n/2) + log n

10. T(n) = 2T(n/2) + n/log n