Introduction
When we study algorithms or data structures, one question always comes –
How fast can we search?
Because in real life applications, searching happens again and again. Finding a student record, Checking whether a product ID exists or Verifying a username during login.
If searching is slow, the entire system becomes slow.
.
From Slow Searching to Fast Searching
- Linear Search
In linear search, we check elements one by one. If there are 10,000 elements, in the worst case we may check all 10,000.
Time Complexity is O(n) so we have to search 10,000 times.

- Binary Search
In binary search, we improve performance. But the condition is that the data must be sorted.
Time Complexity is O(log n)
So performance improved.
But sorting also takes extra effort nearly O(nlogn) time.
Now the goal becomes clear – Can we search in the constant time O(1)?
That is where hashing comes into the picture.
.
What is Hashing?
Hashing is a technique where we do not search for the element step by step. Instead, we calculate the position where the element should be stored.
So if we know the key, we directly go to that location.
This is why hashing can achieve O(1) time in ideal cases.
Example
Suppose we are storing student roll numbers. Assume roll numbers can go up to 10. Now imagine in our class we have only 6 students.
Their roll numbers are:
5, 1, 7, 10, 9, 2
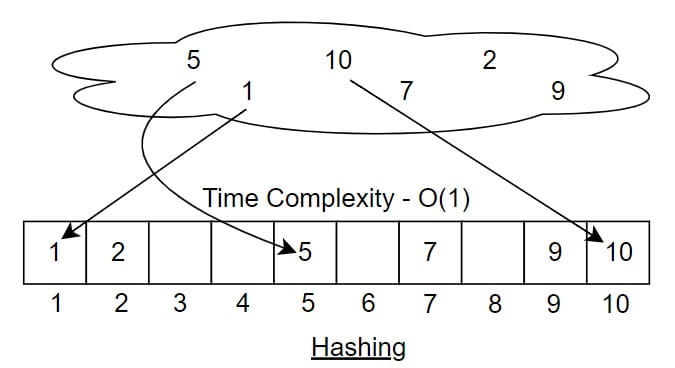
If we want to find the key 10, we do not search one by one. We directly go to index 10 and check whether the key is present there or not. This direct access makes the time complexity O(1). It looks like a very successful and powerful method because searching becomes extremely fast.
But there is a small problem. There is a glitch.
.
Why Direct Indexing is not useful?
If we use direct indexing, and assume that roll numbers can go upto 5000, and imagine that we have a newly come student has a roll number 5000, what will we do?
Store 5 at index 5
Store 1 at index 1
Store 7 at index 7
Store 10 at index 10
Store 9 at index 9
- Store 2 at index 2
Store 5000 at index 5000
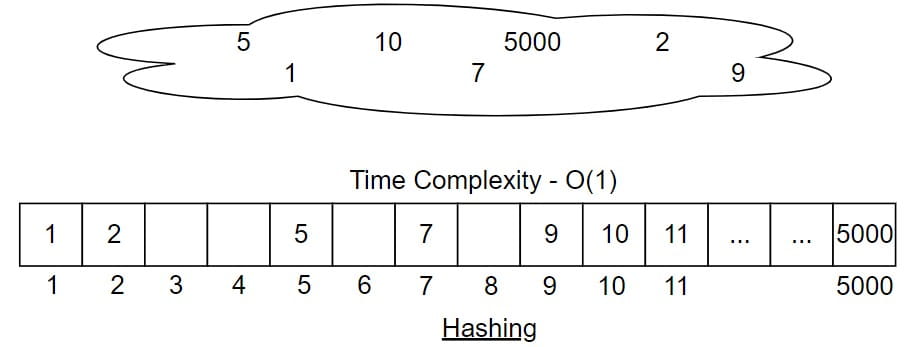
Now think carefully. What size array do we need?
We need an array of size at least 5001.
But how many students do we actually have?
Only 6.
So what about the remaining positions?
All empty.
That means –
Thousands of spaces are unused
Memory is wasted
System becomes inefficient
Yes, searching will be very fast. But space usage becomes very poor. And in real systems, memory is important. That is why direct indexing is not a practical solution.
Instead, we use a hash function to reduce the index range. This is where hashing becomes powerful.
.
Basic Terminology
To understand hashing clearly, we should know three important terms.
Key – The value we want to store or search.
Hash Table – An array where data is stored.
Hash Function – A function that converts a key into an index of the array.
The hash function is the most important part.
A good hash function distributes data properly inside the table.
.
Instead of storing at the actual value index, we use a formula to limit the index range. A common hash function is –
H(x) = x mod m
Where:
- x is the key
- m is the size of the hash table.
Let us take a small example.
Assume the table size is 10.
If the key is 37, then 37 mod 10 = 7
So it will be stored at index 7.
If the key is 52, then 52 mod 10 = 2
So it will be stored at index 2.
In this way, no matter how large the key is,
the index will always be between 0 and 9.

This reduces memory usage and keeps searching fast.
.
Time Complexity of Hashing
1. In Ideal Condition
If the hash function distributes keys uniformly, then,
Search – O(1) because we directly access the computed index.
Insertion – O(1) because we place the key at its calculated index.
Deletion – O(1) because we directly access the key using hash function and remove it.
This constant time complexity is the main advantage of hashing but in the IDEAL CONDITION. If the keys are 52 and 32 both, then it will have a collision. Because 52 mod 10 = 2 and 32 mod 10 = 2. Who will enter and who will not. I will teach in the next part but there is one concept that m should be a prime number because if 52 mod 7 (a prime number) = 3 and the 32 mod 7 = 4. It will create less collision if you have m as a prime number.
.
Pigeonhole Principle in Hashing
In hashing, Keys are like pigeons and Hash table indices are like pigeonholes.
If the number of keys is greater than the number of slots in the hash table, then at least two keys must map to the same index. This situation is called collision. So collision is not a mistake. It is mathematically unavoidable.
.
Collision Handling Techniques
- What is collision
- Open addressing
- Linear probing
- Quadratic probing
- Double hashing
- Separate chaining
- Clustering problem
- Comparison of methods
We will study in the next part of algorithm.
.
Applications of Hashing in Real Life
Hashing is not just a theory topic. It is used in many real systems where we need fast searching and fast access.
When you create an account, your password is not stored directly. It is converted into a hash value and stored in the database.
In large databases, searching a record line by line is very slow.
Hashing is used to create an index, so the system can directly jump to the required record.
3. Compiler Design – Symbol Table
In compilers, variables and function names are stored in a symbol table.
Hashing is used to quickly check whether a variable is already declared and what is its type. This makes compilation faster.
4. Caching Systems
Web browsers and servers use hashing in caching. When you visit a website, data is stored in cache. Hashing helps to quickly check whether data already exists in cache.
5. Searching in Data Structures
Languages like Python (dictionary), Java (HashMap) and C++ (unordered_map) are all use hashing internally to provide O(1) average time for search and insertion.
Hashing is used to detect duplicate files and detect duplicate records and also remove repeated elements from a list because hashing makes comparison very fast.
Test Yourself
Q1- If direct indexing is used for storing 6 students with roll numbers 5, 18, 72, 450, 999, 5000, what is the minimum required array size?
6
1000
5001
999
Ans – (3)
Explanation – In direct indexing, the index is equal to the key. Since the largest roll number is 5000, we need an array that can store index 5000. Array indexing starts from 0, so size must be at least 5001. This shows why direct indexing wastes memory.
Q2- Which of the following is the main drawback of direct indexing?
Slow searching
Complex implementation
High memory usage
High time complexity
Ans – (3)
Explanation – Direct indexing gives O(1) search, so time is good. But if key range is large and actual data is small, memory is heavily wasted. That is the main limitation.
Q3- Why is m often chosen as a prime number in H(x) = x mod m?
To increase memory
To remove collision completely
To increase time complexity
To reduce clustering and collision
Ans – (4)
Explanation – Prime table size helps distribute keys more uniformly. It does not remove collision completely but reduces the probability.
Q4- If the number of keys is greater than table size, collision is:
Optional
Rare
Impossible
Guaranteed
Ans – (4)
Explanation – By Pigeonhole Principle, if keys > slots, at least two keys must share a slot. So collision is guaranteed.
Q5- In ideal hashing condition, time complexity of search is:
O(n)
O(log n)
O(1)
O(n log n)
Ans – (3)
Explanation – If hash function distributes uniformly and no heavy collision occurs, search, insert, delete all become O(1).
Q6- Which condition makes hashing degrade to O(n)?
Sorted data
All keys map to same index
Large table size
Prime table size
Ans – (2)
Explanation – If all keys collide at one index, then we must scan linearly inside that bucket. That becomes O(n).
Q7- Which statement is true?
Collision means hash function is wrong
Collision can be avoided completely
Collision is mathematically unavoidable
Collision occurs only when table is full
Ans – (3)
Explanation – By Pigeonhole Principle, collision is unavoidable. It is not a mistake, it is a mathematical property.
Q8- Explain how hashing reduces memory wastage compared to direct indexing.
Ans – Hashing uses a hash function to map large keys into a smaller index range. Instead of using actual key value as index, we compute H(x) = x mod m. This limits index between 0 and m−1. So even if key is very large, it is stored within fixed table size. This reduces memory wastage significantly.
Q9- Explain the importance of prime number table size.
Ans – When table size is prime, modulo operation distributes keys more uniformly. It reduces patterns and clustering. It does not remove collision completely but reduces probability of repeated collisions.
Q10- Compare linear search, binary search, and hashing.
Ans – Linear search has O(n) time. Binary search improves to O(log n) but requires sorted data. Hashing provides O(1) average time without needing sorted data. However, hashing may degrade to O(n) in worst case.
Q11- Explain why hashing is suitable for real-time systems.
Ans – Hashing provides O(1) average time for search and insertion. In real-time systems like caching, login verification, database lookup, fast response is required. Hashing ensures constant time access in most practical cases.






