Let’s see the insertion sort.
1 This is a very simple sort.
2 There is an unsorted array in which we first take the item and put it in the sorted array.

3 In this sort, the number of inputs should be less, if there are more numbers, then the time complexity will increase very much in the worst case.
Working of Insertion Sort
You must have played playing cards and even if you have not played, it does not matter.
Let’s say that you are playing cards and you have 8 cards, which are inverted on the table so that no one else knows which cards you have. One thing to remember in this is that the cards kept on the table are your input, meaning there are 8 cards, then there is an input of 8 numbers.
Now you picked up the index 1 card from your right hand and placed it in your left hand without showing it to anyone Because it is only one card, it will be already sorted. Do not think too much about the right hand or left hand, listen carefully.

Now you picked up the second card and the second card is bigger than the first card, then you put the second card on the right side of the first card. Most people put cards by sorting.

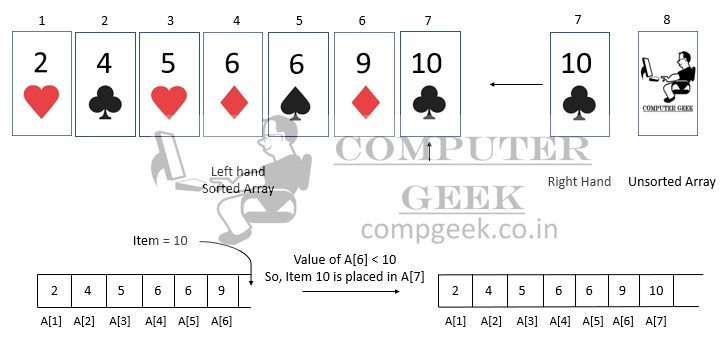
Important – Whenever we have to insert a card, we will visit the sorted output array from the right side because we are using the array and we know how many numbers or cards we have put in the output array.
In the above diagram, when we remove the third card, we will first compare it to A[2] and then to A[1] because we know that we have already put two cards in the output array. If the card in the right hand is smaller than the card in the sorted output array, then we will compare it with the card smaller than that which you will find on the left-hand side and if the card in the right hand is bigger than or equal to the card in the left hand, then we will keep it in the right of the card that compares.
Now pick up your third card and the number of the third card is the largest, so put it on the right side of those two cards in your left hand. You are putting those cards in your left hand while sorting.
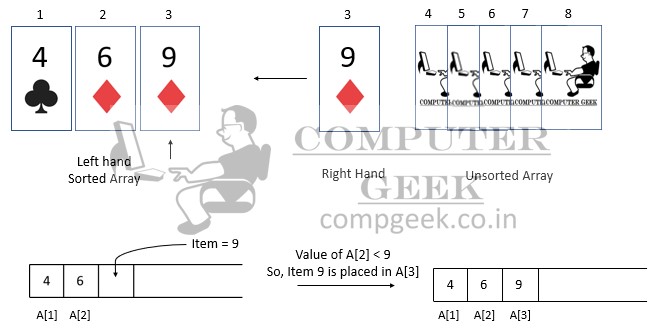
Now there are three cards in your left hand, the middle card is a diamond of 6 numbers and the fourth card you picked up is 6 number spades. So where will you put it, before or after the diamond of 6? You have to put the fourth card only after the diamond of 6. Why?
Because when we design the definition of the insertion sort, we travel or access from the right-hand side of the sorted output array.
We will put the fourth card given in the input i.e. the 6-number spade at number three in the output.
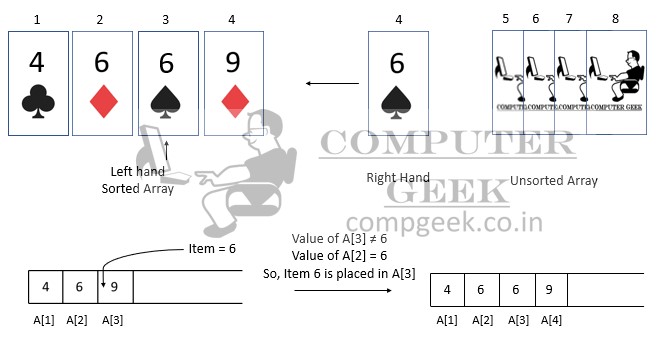
Now pick up the fifth card whose number is 5 of heart and to put it, we will compare it with the right side in the left hand. A[4] has a value of 9 and 9 > 5 so we will go to A[3]. its value is 6 and 6 > 5 so we will go to A[2]. A[2] value is 6 and 6 > 5 so we will go to A[1]. A[1] has a value of 4 and 4 < 5, then we will place 5 of heart in A[2] and shift all other elements right.
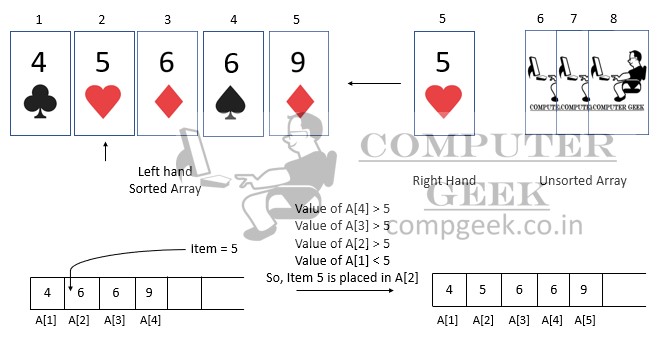
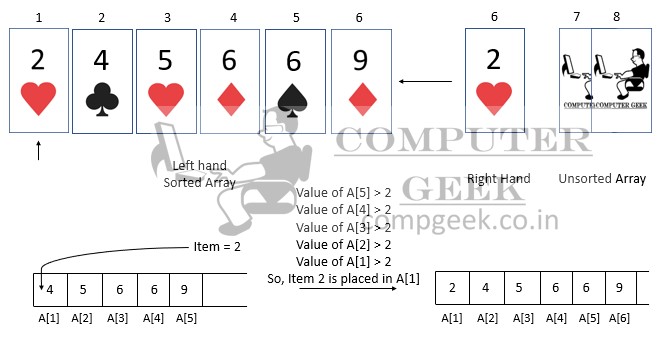
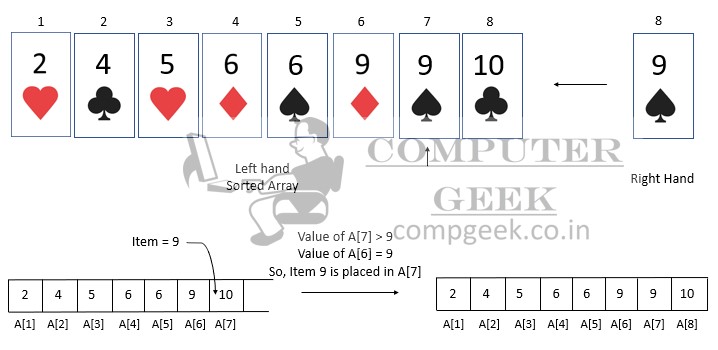
After that, we will apply for the 6th, 7th, and 8th cards in the same way.
Unsorted input array is Y[i], i= 1
Sorted output array is X[j], j = 0
- Y[1] = X[j+1]
- for Y[2] to Y[n] execute statement 3-5
- Compare and insert Y[i] into sorted output array X[1…j] from right
- If (j>0 && X[j] > Y[i]), j = j – 1;
- else, Right shift all the values from X[j+1] to end of sorted output array and Place Y[i] = X[j+1];
- Y[1] = X[j+1]
We will place the value of index 1 of the unsorted input array in index 1 of the sorted output array. That value will be sorted because there is no value in the output array with which we can compare and only one value is always sorted.
- for Y[2] to Y[n] execute statements 3-5
This means that for all the values in the unsorted input array from index 2 to index n, we have to execute from statement 3 to statement 5 (depending on which condition is correct).
- Compare and insert Y[i] into sorted output array X[1…j] from right
Whatever value is derived from the unsorted input array, we will compare it to the right side in the sorted output array and place it in the right place so that the output array is sorted after adding the item value. If the sorted output array is 4, 6, 10, 15, 16 then we will first compare Y[i] by 16
- If (j>0 && X[j] > Y[i]), j = j – 1;
If j > is 0 and the value of the sorted output array, X[j] is greater than Y[i] then j = j – 1 statement will run.
- else, Place Y[i] = X[j+1] and right shift all the values from X[j+1] to end of sorted output array;
If the condition in the 4th statement is false, then the else condition will run. The value of Y[i] will come in X[j+1] and if there is a value in X[j+1], it will be right-shifted.
Program of Insertion sort in C
Enter the 6 items of the array : 1 2 6 5 3 4
Sorted array : 1 2 3 4 5 6
Time Complexity of Insertion Sort
- In the Best Case, the time complexity is O(n)
Reason – In the best case, all the values in unsorted input array are already sorted.
- In the Worst Case, the time complexity is O(n2)
Reason – In the worst case, all the values in unsorted input array are distinct and non-decreasing.
- In the Average Case, the time complexity is O(n2)
Space Complexity is O(1) as needed for swapping.
The idea behind calculation of time complexity
The actual time complexity is O(n + p). where p is the number of inversions.
Let’s say the input is 6, 5, 4, 2, 1
Theoretically, the number of inversions in a reverse sorted list is n(n-1)/2
Practically we have number of inversions is
(6,5) -> (5,6)
(6,4) -> (4,6)
(5,4) -> (4,5)
(6,2) -> (2,6)
(5,2) -> (2,5)
(4,2) -> (2,4)
(6,1) -> (1,6)
(5,1) -> (1,5)
(4,1) -> (1,4)
(2,1) -> (1,2)
Number of Input, n = 5
Number of Inversions, p = 10
-> n(n-1)/2 = 10
-> 5(5-1)/2 = 10
-> 10 = 10
Formula of time complexity
= O(n + p) = O(n + n(n-1)/2))
discarding lower order term
= O(n2)
Most Important – It is unnecessary to put the constant in O(n + p) as O(5 + 10) as you didn’t get the result. You have to put everything in the variable n and show the time complexity in the terms of n.
Advantages of Insertion Sort
- It is a very simple algorithm
- Humans always use this technique to sort anything.
- Efficient on small inputs.
- It is in-place sort as requires a constant amount of space O(1).
- It is a stable sort as well.
Test Yourself
Q1- What is the best-case time complexity of Insertion Sort, and when does it occur?
The best-case time complexity of Insertion Sort is O(n). This occurs when the input array is already sorted in ascending order. In such a scenario, Insertion Sort simply checks each element and places it in its correct position without the need for any swaps. As a result, the time complexity reduces to linear, making it the best case for this algorithm.
Q2- Explain the concept of “inversions” in the context of Insertion Sort.
Inversions refer to the pairs of elements in an array that are not in the correct order with respect to the desired sorted order. For a given array, if the current element is greater than any element that appears later in the array, it creates an inversion. The number of inversions in an array indicates how much “out of order” the array is.
In the context of Insertion Sort, the number of inversions plays a role in determining the time complexity. The worst-case time complexity of Insertion Sort is O(n2), and the number of inversions in the input array affects the performance. An array that is already sorted or nearly sorted (few inversions) will result in a better time complexity, while an array with a large number of inversions will lead to a higher time complexity.
Q3- In which case does Insertion Sort perform the best?
When the input array is already sorted in ascending order.
When the input array is already sorted in descending order.
When the input array is unsorted.
When the input array contains duplicate elements.
Ans – (1)
Q4- Which of the following statements is true about Insertion Sort?
It is an unstable sorting algorithm.
It has a time complexity of O(n log n) in all cases.
It is an in-place sorting algorithm.
It performs poorly on small input sizes.
Ans – (3)
Explanation – Insertion Sort is an in-place sorting algorithm, which means it does not require any additional memory to perform the sorting. The sorting is done by rearranging the elements within the input array itself, making it an efficient choice when memory usage is a concern.
Q5- Describe a situation where using Insertion Sort would be advantageous over more advanced sorting algorithms like Quick Sort or Merge Sort.
Insertion Sort can be advantageous over more advanced sorting algorithms like Quick Sort or Merge Sort in scenarios where the input size is small or when the data is already partially sorted.
Small Input Size: When dealing with a small number of elements, the overhead of more complex algorithms like Quick Sort or Merge Sort can outweigh their advantages. Insertion Sort has a simple implementation and constant space complexity, making it faster and more efficient for sorting a small number of elements.
Partially Sorted Data: If the input data is partially sorted or contains a significant number of elements in their correct order, Insertion Sort can take advantage of this property. The algorithm will perform fewer comparisons and swaps, making it faster than other sorting algorithms that don’t take advantage of the partial ordering.






