Heap is a tree-based data structure where all tree nodes are organized to follow a predefined parent-child relationship.
It makes a comparison between the parent node value and its child node value. If it is not in sorted order, then we swap the values to make it a heap.
Heap sort is a comparison-based sorting method.
First, we follow the rules and keep the maximum value on the root, then we delete and store the root value and make that tree-like structure heap again. When the maximum value is on the root again, we delete and store the root again, and this process is done until the array is over.
In the storage, the maximum value gets the highest position because it is deleted first, and the minimum value gets the lowest position because it is deleted last.
- In 1964, heap sort was invented by John Williams.
- It is a tree-based structure means it does not waste time arranging the elements in a linear scan of the unsorted array.
- We generally use binary heap tree whose root contains left child and right child.
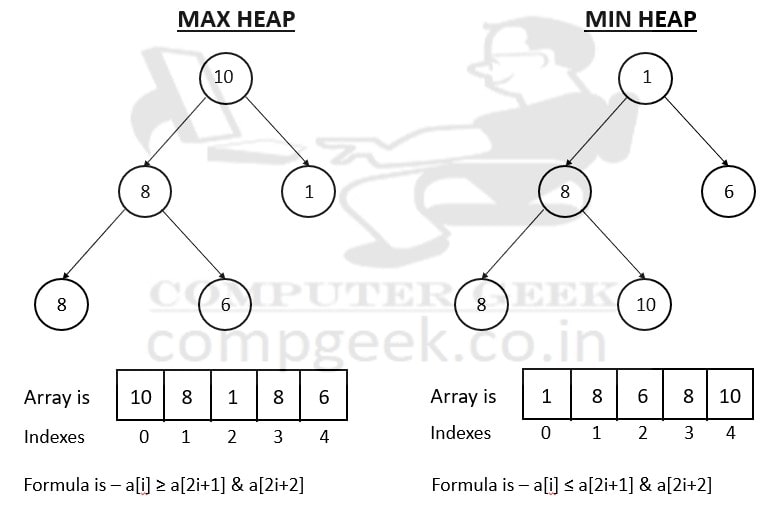
- The Heap is of two types: Max-heap and Min-heap.
The root node value in Max-heap is greater than or equal to every child node value.
If i variable represents the index, then a[i] ≥ a[2i+1] & a[2i+2]
The root node value in Min-heap is smaller than or equal to every child node value.
If the i variable represents the index, then a[i] ≤ a[2i+1] & a[2i+2].
- If heap is ternary tree, then the formula a[i] ≤ a[3i+1], a[3i+2] & a[3i+3] is applied.
Rule for Inserting in a heap
- We make heap like a complete binary tree.
- There are two ways in which we can make a complete binary tree into a heap.
Complete binary tree –
It is a binary tree with the maximum number of nodes on each level except the last, which has nodes from left to right.
Suppose we are making a max heap and input array is
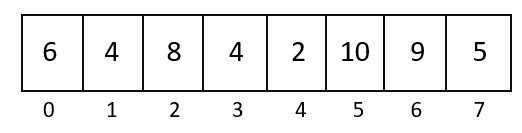
(i) Make a binary tree by scratch. First, put the index 0 value as root. Now make index 1 value as the left child of the root. Compare it. If the child value is larger than the parent value, then swap it.
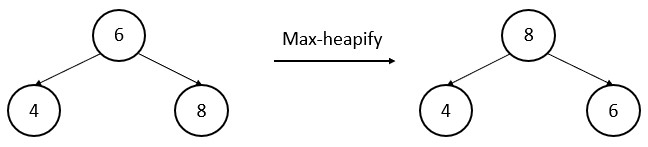
Means by inserting an input array number, we find its correct position by the rules. It is called a heapify (top to bottom). The time complexity of top to bottom heapify is O(logn).
(ii) Make a complete binary tree with all the input numbers we have and apply the heapify (bottom-to-top) algorithm. The time complexity of bottom to top heapify is O(1). It is less than top-to-bottom heapify.
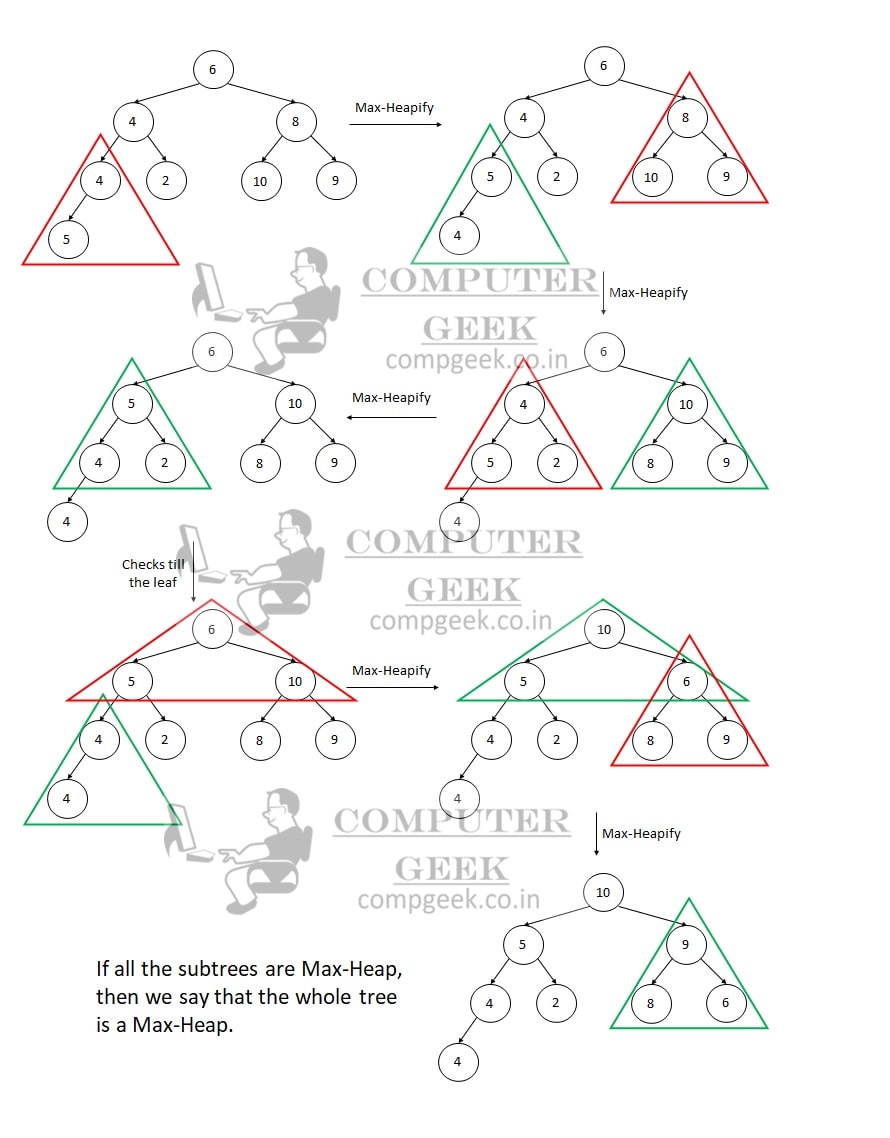
Max-heapify(a, i)
Left <– a[2i]
Right <– a[2i+1]
If (Left ≤ size of array && a[left] > root a[i])
Largest_no <– left
Else
Largest_no <– i
If Right ≤ size of array && a[Right] > a[Largest_no]
Largest_no <– Right
If Largest_no ≠ root i
Swap(a[i], Largest_no)
Max-heapify(a, Largest_no)
Size of array <– a[].length
int i;
for(i = a[].length/2; i ≥ 1; i–)
max-heapify(a[], i)
Test Yourself
Q1- Explain the concept of a binary heap and its two types, Max-heap and Min-heap.
A binary heap is a tree-based data structure where all nodes follow a specific parent-child relationship. In a Max-heap, the value of each parent node is greater than or equal to the values of its child nodes. Conversely, in a Min-heap, the value of each parent node is smaller than or equal to the values of its child nodes. The root node holds the maximum (in Max-heap) or minimum (in Min-heap) value.
Q2- Describe the process of inserting a new element into a Max-heap.
To insert a new element into a Max-heap, the element is initially placed at the last position of the binary tree, which maintains the complete binary tree property. Then, the “heapify” operation (bottom-to-top heapify) is performed to compare the newly inserted element with its parent node and swap them if the parent’s value is less than the child’s value. This process continues until the element reaches its correct position in the Max-heap.
Q3- Compare the time complexities of top-to-bottom heapify and bottom-to-top heapify operations.
The time complexity of top-to-bottom heapify is O(logn), where “n” is the number of nodes in the heap. However, the time complexity of bottom-to-top heapify is O(1), which means it is more efficient than the top-to-bottom heapify operation. The bottom-to-top heapify is used during the building of the heap.
Q4- What is a complete binary tree, and why is it used in the heap data structure?
A complete binary tree is a binary tree in which all levels, except possibly the last one, are filled, and the nodes are filled from left to right on the last level. Complete binary trees are used in the heap data structure because they help to efficiently store elements in an array without wasting space. The elements of the heap can be easily mapped to the positions in the array, making access and manipulation more straightforward.
Q5- Explain the concept of building a max-heap and the role of the “max-heapify” operation.
Building a max-heap involves converting a complete binary tree into a valid max-heap. The process starts from the first non-leaf node and applies the “max-heapify” operation to ensure that each parent node contains a value greater than or equal to its child nodes. This process is performed in a bottom-to-top manner, resulting in a valid max-heap representation of the input array.
Q6- Can a binary heap be used to efficiently find the kth smallest or kth largest element in an array? Explain.
Yes, a binary heap can be used to efficiently find the kth smallest or kth largest element in an array. For finding the kth smallest element, a Max-heap can be used, where the root node holds the maximum value. By extracting the maximum element (k times) and applying “max-heapify” after each extraction, the kth smallest element can be found. Similarly, for finding the kth largest element, a Min-heap can be used, where the root node holds the minimum value, and the process is repeated accordingly.
Q7- Heap sort was invented by:
John Williams
John von Neumann
Donald Knuth
Alan Turing
Ans – (1)
Q8- What is the parent-child relationship in a binary max-heap?
Parent is greater than both children.
Parent is greater than or equal to both children.
Parent is smaller than both children.
Parent is smaller than or equal to both children.
Ans – (2)
Explanation – In a binary max-heap, the parent node’s value is greater than or equal to its child nodes’ values.
Q9- Which type of heapify operation is more efficient – top-to-bottom or bottom-to-top?
Top-to-bottom
Bottom-to-top
Both have the same efficiency
It depends on the heap size
Ans – (2)
Explanation – Bottom-to-top heapify is more efficient as it starts from the last non-leaf node and requires fewer comparisons and swaps compared to top-to-bottom heapify.






