Introduction
.
A Hamiltonian cycle is a special type of cycle in a graph that visits every vertex exactly once and returns to the starting vertex.
Unlike a Eulerian cycle, which visits every edge, a Hamiltonian cycle focuses on visiting every vertex. The challenge of finding such a cycle in a graph is known as the Hamiltonian cycle problem.
.
Early Concepts and Origins
Sir William Rowan Hamilton (1805–1865) – The Hamiltonian cycle is named after the Irish mathematician Sir William Rowan Hamilton, who introduced the concept in the 19th century.
Hamilton devised a mathematical game known as the “Icosian Game” where he sought to find a cycle that passes through each vertex of a dodecahedron (a polyhedron with twelve faces) exactly once before returning to the starting point. His work laid the foundation for the Hamiltonian cycle concept in graph theory.
The Hamiltonian cycle problem was formalized as a computational problem during the rise of computer science in 1960s – 1970s. This period saw the development of algorithms and computational complexity theory. The problem was identified as NP-complete, meaning it is computationally hard to solve efficiently for large graphs.
Also, in the 1960s, algorithms for finding Hamiltonian cycles using backtracking were developed. These algorithms systematically explore all possible paths to find a cycle that visits every vertex exactly once.
.
Example – The graph below is a Hamiltonian Graph.
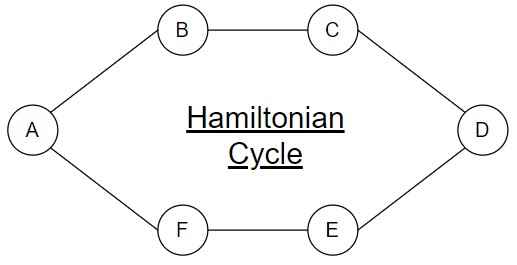
The vertex A, B, C, D, E, F, A is a Hamiltonian cycle.
This problem is particularly interesting because it belongs to the class of NP-complete problems, meaning it is difficult to solve efficiently for large graphs, because there is an exponential time taking problem.
One of the common approaches to solving this problem is through the backtracking algorithm. Backtracking systematically explores all possible paths in the graph and eliminates those that do not lead to a valid Hamiltonian cycle.
.
Example – Find all possible combinations of Hamiltonian Cycles in the below graph.
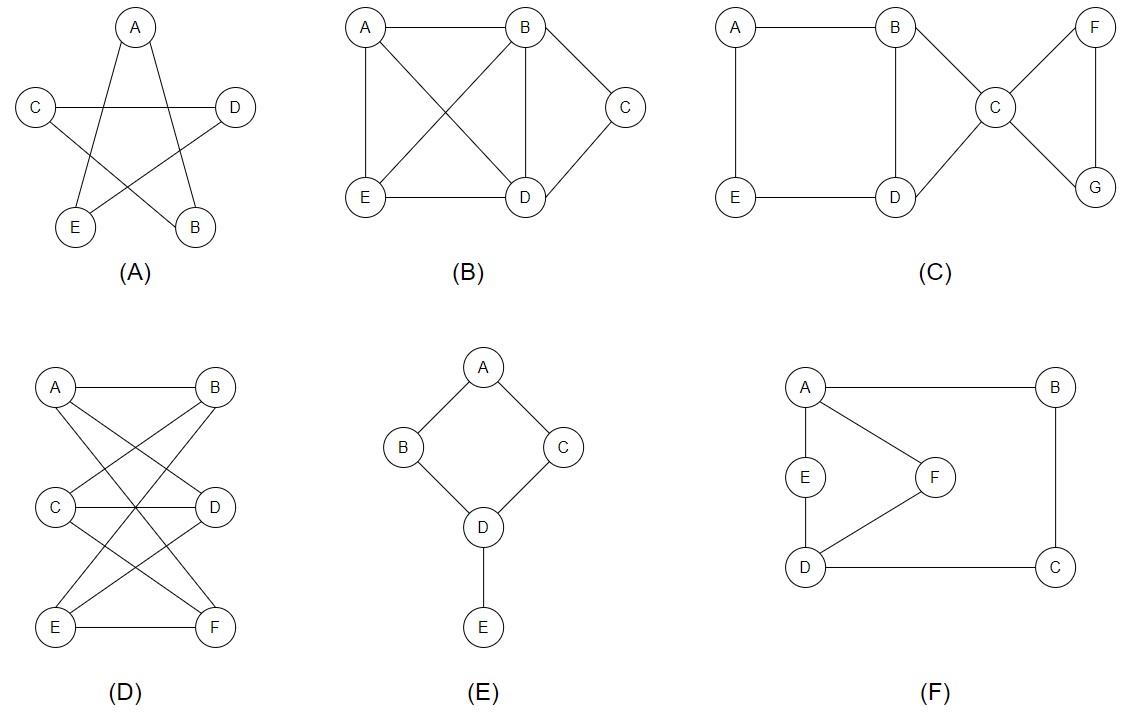
.
Graph (A)
All possible solutions of Hamiltonian Cycles include only one cycle in the above graph, A, B, C, D, E, A.
However, B, C, D, E, A, B is essentially the same as this Hamiltonian cycle, so it does not count as a second Hamiltonian cycle.
.
Graph (B)
This graph is a pentagon with an inner star-shaped structure Hamiltonian Cycle1 – A, B, C, D, E, A
Hamiltonian Cycle 2 – A, D, C, B, E, A
.
Graph (C)
This graph has two triangles connected by a rectangle. The vertex C is called the articulation point of the graph. These types of graphs do not contain Hamiltonian Cycle.
.
Graph (D)
This is a bipartite graph, and it contains a Hamiltonian Cycle A, B, C, D, E, F, A.
Graph (E)
In this graph, there is a vertex E which is called the pendant vertex, and these pendant graphs do not contain Hamiltonian Cycle.
.
Graph (F)
The graph has no Hamiltonian Cycles.
.
Algorithm of Finding All Hamiltonian Cycles
Initialization
- Create an empty list to store all Hamiltonian cycles.
- Create a path array to store the current path being explored.
- Initialize all vertices as unvisited.
Recursive Function – findCycles(v, path)
- If all vertices are visited and there is an edge from the last vertex in the path back to the first vertex, then
- Add the first vertex to the end of the path (to complete the cycle).
- Save this path as a Hamiltonian cycle.
- Remove the first vertex from the end of the path (to continue searching for other cycles).
- If all vertices are visited but there is no edge from the last vertex back to the first, then backtrack (return).
- For each unvisited adjacent vertex u of v
- Mark u as visited.
- Add u to the path.
- Recur with findCycles(u, path).
- Backtrack by removing u from the path and marking it as unvisited.
Start the Algorithm
- Start from any vertex (say vertex 0) and call findCycles(0, path).
- Return the list of Hamiltonian cycles.
.
Example – The Hamiltonian graph for backtrack is
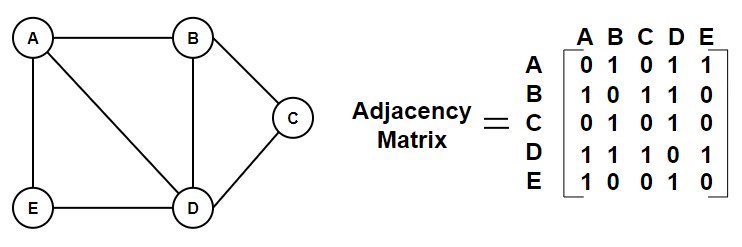
.
Step 1 – Create a path array to store the current path being explored. Initialize all vertices as unvisited (0).
Hamiltonian Cycle – {0, 0, 0, 0, 0}
.
Step 2 – Start at vertex A as the stating vertex.
Hamiltonian Cycle – {A, 0, 0, 0, 0}
.
![]()
.
Step 3 – In adjacency list, for the current vertex A, look at all the connected vertices (where 1 is present). Here, vertices B, D, and E are connected to A because the matrix has 1 in those positions.
Hamiltonian Cycle – {A, 0, 0, 0, 0}
.
Step 4 – Next, we take B connected vertices because B is in extreme left.
Hamiltonian Cycle – {A, B, 0, 0, 0}
.
Step 5 – Next, we take C connected vertices because C is in the extreme left.
This goes on and on …
The full backtracking tree is –
![]()
Hamiltonian Cycle 1 – A, B, C, D, E, A
Hamiltonian Cycle 2 – A, E, D, C, B, A
The second cycle is just reverse of the first cycle. If the graph is directed graph, then the reverse case will not apply.
.
Source Code for Hamiltonian Cycle Problem
// COMPUTER GEEK – compgeek.co.in
// Write a program for All possible Hamiltonian Cycle with backtracking
#include <stdio.h>
#include <stdbool.h>
#define MAX 20
int path[MAX]; // Store vertices in the current Hamiltonian path
int V; // Number of vertices
// Function to print the Hamiltonian cycle
void printCycle() {
for (int i = 0; i < V; i++) {
printf(“%d “, path[i] + 1); // Print vertex numbers starting from 1
}
printf(“%d\n”, path[0] + 1); // Print the starting vertex to complete the cycle
}
// Function to check if the current vertex can be added to the path
bool isSafe(int v, bool graph[MAX][MAX], int pos) {
// Check if this vertex is an adjacent vertex of the previous vertex
if (graph[path[pos – 1]][v] == 0)
return false;
// Check if the vertex is already included in the path
for (int i = 0; i < pos; i++)
if (path[i] == v)
return false;
return true;
}
// Recursive utility function to solve the Hamiltonian cycle problem
bool hamiltonianCycleUtil(bool graph[MAX][MAX], int pos) {
// If all vertices are included in the cycle
if (pos == V) {
// And if there is an edge from the last vertex to the first vertex
if (graph[path[pos – 1]][path[0]] == 1)
return true;
else
return false;
}
// Try different vertices as the next candidate in the Hamiltonian cycle
for (int v = 1; v < V; v++) {
// Check if this vertex can be added to the Hamiltonian cycle
if (isSafe(v, graph, pos)) {
path[pos] = v;
// Recur to construct the rest of the path
if (hamiltonianCycleUtil(graph, pos + 1) == true) {
printCycle();
}
// Remove the current vertex if it doesn’t lead to a solution
path[pos] = -1;
}
}
return false;
}
// Function to solve the Hamiltonian cycle problem using backtracking
void hamiltonianCycle(bool graph[MAX][MAX]) {
// Initialize the path array
for (int i = 0; i < V; i++)
path[i] = -1;
// Let the first vertex in the path be vertex 0
path[0] = 0;
// Call the recursive utility function to solve the problem
hamiltonianCycleUtil(graph, 1);
}
// Main function to take input and find all Hamiltonian cycles
int main() {
bool graph[MAX][MAX];
// Take input for the number of vertices
printf(“Enter the number of vertices: “);
scanf(“%d”, &V);
// Take input for the adjacency matrix
printf(“Enter the adjacency matrix:\n”);
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
scanf(“%d”, &graph[i][j]);
}
}
// Find all Hamiltonian cycles
printf(“Hamiltonian cycles are:\n”);
hamiltonianCycle(graph);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for All possible Hamiltonian Cycle with backtracking
#include <iostream>
#include <vector>
using namespace std;
#define MAX 20
int V; // Number of vertices
vector<int> path; // Store vertices in the current Hamiltonian path
// Function to print the Hamiltonian cycle
void printCycle() {
for (int i = 0; i < V; i++) {
cout << path[i] + 1 << ” “; // Print vertex numbers starting from 1
}
cout << path[0] + 1 << endl; // Print the starting vertex to complete the cycle
}
// Function to check if the current vertex can be added to the path
bool isSafe(int v, vector<vector<int>>& graph, int pos) {
// Check if this vertex is an adjacent vertex of the previous vertex
if (graph[path[pos – 1]][v] == 0)
return false;
// Check if the vertex is already included in the path
for (int i = 0; i < pos; i++)
if (path[i] == v)
return false;
return true;
}
// Recursive utility function to solve the Hamiltonian cycle problem
bool hamiltonianCycleUtil(vector<vector<int>>& graph, int pos) {
// If all vertices are included in the cycle
if (pos == V) {
// And if there is an edge from the last vertex to the first vertex
if (graph[path[pos – 1]][path[0]] == 1)
return true;
else
return false;
}
// Try different vertices as the next candidate in the Hamiltonian cycle
for (int v = 1; v < V; v++) {
if (isSafe(v, graph, pos)) {
path[pos] = v;
// Recur to construct the rest of the path
if (hamiltonianCycleUtil(graph, pos + 1)) {
printCycle();
}
// Remove the current vertex if it doesn’t lead to a solution
path[pos] = -1;
}
}
return false;
}
// Function to solve the Hamiltonian cycle problem using backtracking
void hamiltonianCycle(vector<vector<int>>& graph) {
path.assign(V, -1); // Initialize the path array
path[0] = 0; // Let the first vertex in the path be vertex 0
hamiltonianCycleUtil(graph, 1);
}
// Main function to take input and find all Hamiltonian cycles
int main() {
cout << “Enter the number of vertices: “;
cin >> V;
vector<vector<int>> graph(V, vector<int>(V));
cout << “Enter the adjacency matrix:\n”;
for (int i = 0; i < V; i++)
for (int j = 0; j < V; j++)
cin >> graph[i][j];
cout << “Hamiltonian cycles are:\n”;
hamiltonianCycle(graph);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for All possible Hamiltonian Cycle with backtracking
import java.util.Scanner;
public class HamiltonianCycle {
private int V; // Number of vertices
private int[] path; // Store vertices in the current Hamiltonian path
// Function to print the Hamiltonian cycle
private void printCycle() {
for (int i = 0; i < V; i++) {
System.out.print((path[i] + 1) + ” “); // Print vertex numbers starting from 1
}
System.out.println(path[0] + 1); // Print the starting vertex to complete the cycle
}
// Function to check if the current vertex can be added to the path
private boolean isSafe(int v, int[][] graph, int pos) {
// Check if this vertex is an adjacent vertex of the previous vertex
if (graph[path[pos – 1]][v] == 0)
return false;
// Check if the vertex is already included in the path
for (int i = 0; i < pos; i++)
if (path[i] == v)
return false;
return true;
}
// Recursive utility function to solve the Hamiltonian cycle problem
private boolean hamiltonianCycleUtil(int[][] graph, int pos) {
// If all vertices are included in the cycle
if (pos == V) {
// And if there is an edge from the last vertex to the first vertex
return graph[path[pos – 1]][path[0]] == 1;
}
// Try different vertices as the next candidate in the Hamiltonian cycle
for (int v = 1; v < V; v++) {
if (isSafe(v, graph, pos)) {
path[pos] = v;
// Recur to construct the rest of the path
if (hamiltonianCycleUtil(graph, pos + 1)) {
printCycle();
}
// Remove the current vertex if it doesn’t lead to a solution
path[pos] = -1;
}
}
return false;
}
// Function to solve the Hamiltonian cycle problem using backtracking
public void hamiltonianCycle(int[][] graph) {
path = new int[V];
for (int i = 0; i < V; i++) {
path[i] = -1;
}
path[0] = 0; // Let the first vertex in the path be vertex 0
hamiltonianCycleUtil(graph, 1);
}
// Main function to take input and find all Hamiltonian cycles
public static void main(String[] args) {
HamiltonianCycle hc = new HamiltonianCycle();
Scanner sc = new Scanner(System.in);
System.out.print(“Enter the number of vertices: “);
hc.V = sc.nextInt();
int[][] graph = new int[hc.V][hc.V];
System.out.println(“Enter the adjacency matrix:”);
for (int i = 0; i < hc.V; i++) {
for (int j = 0; j < hc.V; j++) {
graph[i][j] = sc.nextInt();
}
}
System.out.println(“Hamiltonian cycles are:”);
hc.hamiltonianCycle(graph);
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for All possible Hamiltonian Cycle with backtracking
def printCycle(path):
for vertex in path:
print(vertex + 1, end=” “) # Print vertex numbers starting from 1
print(path[0] + 1) # Print the starting vertex to complete the cycle
def isSafe(v, graph, path, pos):
# Check if this vertex is an adjacent vertex of the previous vertex
if graph[path[pos – 1]][v] == 0:
return False
# Check if the vertex is already included in the path
if v in path:
return False
return True
def hamiltonianCycleUtil(graph, path, pos):
# If all vertices are included in the cycle
if pos == len(graph):
if graph[path[pos – 1]][path[0]] == 1:
printCycle(path)
return True
else:
return False
# Try different vertices as the next candidate in the Hamiltonian cycle
for v in range(1, len(graph)):
if isSafe(v, graph, path, pos):
path[pos] = v
# Recur to construct the rest of the path
if hamiltonianCycleUtil(graph, path, pos + 1):
# Only to print all cycles, not just one solution
pass
# Remove the current vertex if it doesn’t lead to a solution
path[pos] = -1
return False
def hamiltonianCycle(graph):
path = [-1] * len(graph)
path[0] = 0 # Let the first vertex in the path be vertex 0
hamiltonianCycleUtil(graph, path, 1)
# Main function to take input and find all Hamiltonian cycles
def main():
V = int(input(“Enter the number of vertices: “))
graph = []
print(“Enter the adjacency matrix:”)
for i in range(V):
graph.append(list(map(int, input().split())))
print(“Hamiltonian cycles are:”)
hamiltonianCycle(graph)
if __name__ == “__main__”:
main()
Enter the number of vertices: 5
Enter the adjacency matrix:
0 1 0 1 1
1 0 1 1 0
0 1 0 1 0
1 1 1 0 1
1 0 0 1 0
Hamiltonian cycles are:
1 2 3 4 5 1
1 5 4 3 2 1
=== Code Execution Successful ===
Time complexity
The time complexity for finding all Hamiltonian cycles in an undirected graph using backtracking is generally discussed in the context of the worst case is O(V!), where V is the number of vertices in the graph.
In the best case, time complexity is O(V) if the graph is extremely sparse or if no Hamiltonian cycle is found early in the search.
In average case, the algorithm might be able to prune some branches of the search tree early, especially in sparser graphs where fewer Hamiltonian cycles exist.
However, the average-case complexity is still dominated by the factorial growth due to the large number of possible vertex orderings that must be checked. Therefore, it is often considered to be O(V!) as well.
.
Space Complexity
Since the algorithm uses backtracking, the recursion depth is equal to the number of vertices V. Therefore, the space required for the recursion stack is O(V).
The algorithm needs to store the current path being explored, which requires O(V) space.
An additional array is used to keep track of which vertices have been visited, which also requires O(V) space.
Therefore, the space complexity for finding all Hamiltonian cycles using backtracking is O(V).
.
Applications of the Hamiltonian Cycle problem
- Network Design – In designing computer networks, finding a Hamiltonian cycle can help in ensuring that every node (router or switch) is visited exactly once, optimizing the efficiency of data transmission.
- Tourism and Travel – For planning tours or travel routes where each city or location needs to be visited exactly once and return to the starting point, Hamiltonian cycles can help find the optimal route.
- Circuit Design – In electronic circuit design, Hamiltonian cycles can be used to layout circuits so that each component is connected in an efficient manner, minimizing the total length of wiring needed.
- Robot Path Planning – For robots that need to cover a grid or map visiting each location exactly once and return to the starting point, finding a Hamiltonian cycle can assist in planning the robot’s path.
- Puzzles and Games – Many puzzles and games, like certain variations of the Travelling Salesman Problem (TSP) or Hamiltonian path games, use Hamiltonian cycles to create challenging and interesting scenarios.
Test Yourself
Q1- Explain what a Hamiltonian cycle is and how it differs from a Eulerian cycle.
A Hamiltonian cycle is a cycle in a graph that visits every vertex exactly once and returns to the starting vertex.
Unlike a Eulerian cycle, which covers every edge of the graph exactly once, a Hamiltonian cycle focuses on visiting each vertex exactly once.
Q2- Describe the backtracking approach to finding Hamiltonian cycles.
The backtracking approach systematically explores all possible paths in the graph.
It starts at a vertex, adds adjacent vertices to the path one by one, and backtracks if a vertex cannot be added without violating the Hamiltonian cycle conditions.
Q3- Why is the Hamiltonian cycle problem classified as NP-complete?
The Hamiltonian cycle problem is NP-complete because there is no known polynomial-time algorithm to solve it, and verifying a solution is feasible in polynomial time.
It requires exponential time to explore all possible vertex orderings for large graphs.
Q4- Can a graph with all vertices having odd degrees contain a Hamiltonian cycle?
Not necessarily. The degree of vertices is not the sole determinant of the existence of a Hamiltonian cycle. The cycle depends on whether a path can be formed that visits each vertex exactly once.
Q5- If a Hamiltonian cycle exists in a graph, does it imply that the graph is complete?
No, a Hamiltonian cycle can exist in non-complete graphs.
A complete graph has all possible edges, but a Hamiltonian cycle only requires a path covering all vertices exactly once.
Q6- Can removing an edge from a graph destroy a Hamiltonian cycle?
Yes, if the removed edge is part of the Hamiltonian cycle, it can destroy the cycle by breaking the path that connects all vertices.
Q7- Is a Hamiltonian path also a Hamiltonian cycle?
No, a Hamiltonian path visits all vertices exactly once but does not return to the starting vertex. Only when it returns to the starting vertex does it become a Hamiltonian cycle.
Q8- What is the time complexity of finding all Hamiltonian cycles using backtracking?
O(V)
O(V^2)
O(V!)
O(2^V)
Ans – (3)
Explanation – The factorial time complexity arises due to the need to explore all possible vertex orderings.
Q9- Which of the following graphs does NOT have a Hamiltonian cycle?
Complete graph
Graph with a pendant vertex
Graph with a Hamiltonian path
Cycle graph
Ans – (2)
Explanation – A graph with a pendant vertex cannot have a Hamiltonian cycle because it breaks the necessary cycle structure.
Q10- In a Hamiltonian cycle problem, if a graph has 5 vertices, how many vertices does the path array have?
4
5
6
10
Ans – (2)
Explanation – The path array stores the vertices in the Hamiltonian cycle, so it has the same number of entries as there are vertices in the graph.
Q11- What is the minimum number of vertices required for a graph to have a Hamiltonian cycle?
1
2
3
4
Ans – (3)
Explanation – A minimum of three vertices is needed to form a cycle.
Q12- In the Hamiltonian cycle problem, what happens when all vertices are visited but there is no edge from the last vertex to the first?
The cycle is complete.
The algorithm backtracks.
A new vertex is added.
The cycle is printed.
Ans – (2)
Explanation – Backtracking occurs because the cycle cannot be completed without connecting to the starting vertex.






