Hamiltonian Cycle Problem

Introduction

.

The Hamiltonian Path or Cycle Problem was formalized as a computational problem during the rise of computer science in 1960s – 1970s.

This period saw the development of algorithms and computational complexity theory. The problem was identified as NP-complete, meaning it is computationally hard to solve efficiently for large graphs.

Also, in the 1960s, algorithms for finding Hamiltonian cycles using backtracking were developed. These algorithms systematically explore all possible paths to find a cycle that visits every vertex exactly once.

According to Michael Garey and David S. Johnson’s book Computers and Intractability: A Guide to the Theory of NP-Completeness and Richard Karp’s list of 21 NP-complete problems both the Hamiltonian path problem and the Hamiltonian cycle problem are NP-complete.

.

Problem Statement

1. Hamiltonian Path

• • Given an undirected or directed graph G, a Hamiltonian path is a sequence of edges that visits each vertex exactly once.
  • To check if a Hamiltonian path exists, you need to examine every possible path within the graph and see if one path covers every vertex exactly once.

2. Hamiltonian Cycle

• • In this problem, we must determine if there’s a Hamiltonian cycle in G, a closed path that starts and ends at the same vertex while visiting each vertex exactly once.
  • It’s like a Hamiltonian path, except it requires the path to loop back to the starting point.

.

NP-Completeness

Both the Hamiltonian Path and Cycle problems are NP-complete

• NP – A problem is in NP if, given a solution, it can be verified in polynomial time.
• NP-Complete – A problem is NP-complete if it’s in NP and every other NP problem can be transformed into it in polynomial time.

.

Algorithm for the Hamiltonian Cycle Problem

Due to the NP-completeness, we do not have a polynomial-time algorithm to find a Hamiltonian cycle in a general graph. However, here is a common backtracking approach to tackle the problem.

1. Choose a starting vertex (let’s call it u).
2. Add u to the path and mark it as visited.
3. For each adjacent vertex v of the current vertex, check if v has already been visited in the current path.
4. If it has not been visited, add v to the path and recursively attempt to extend the path from v.
5. If the current path length equals the number of vertices and there’s an edge from the last vertex back to the starting vertex, we’ve found a Hamiltonian cycle.
6. Backtrack if no further extension is possible from the current path.

If we reach a dead end (i.e., we cannot complete a cycle), we backtrack to explore other potential paths.

.

Time Complexity

The time complexity of solving Hamiltonian Path and Cycle problems using backtracking is O(n!). n! tries all possible permutations of vertices, it has factorial time complexity. Because of this exponential growth in time, this approach is impractical for large graphs.

Suppose this is the graph where we have to find out the Hamiltonian path or cycle. We have the algorithm to find out the Hamiltonian cycle or path, but it will take milleniums to generate the correct output.

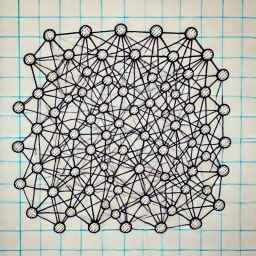
Roughly, this graph has 75 vertices. The time complexity it has is O(n!), and 75! is 1.0314 × 10²⁰⁶. Thus, this problem is np-complete.

.

Reduction of Hamiltonian Path Problem to Hamiltonian Cycle Problem and vice versa.

In both conversions, the modified graph helps transform the nature of the Hamiltonian path or cycle problem while maintaining the graph’s structure, allowing one problem to be solved using a solution to the other. This conversion is in polynomial times and hence if cycle is NP-Complete then path is NP-Complete and vice versa.

.

.

Reduction of 3-SAT to Hamiltonian Cycle Problem

The 3-SAT problem is the first problem that can be proved by scientist, an NP-Complete problem. Reduction of the 3-SAT problem to the Hamiltonian cycle problem will prove that the Hamiltonian cycle problem is also an NP-Complete problem.

To reduce 3-SAT to Hamiltonian Cycle, we need to create a graph where finding a Hamiltonian cycle would be equivalent to finding a satisfying assignment for the 3-SAT formula.

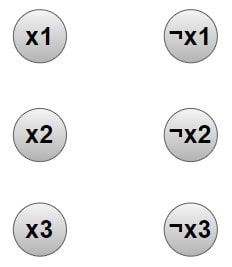
1. For each variable xi in the 3-SAT formula, create two nodes representing the literal xi (true) and ¬xi​ (false).
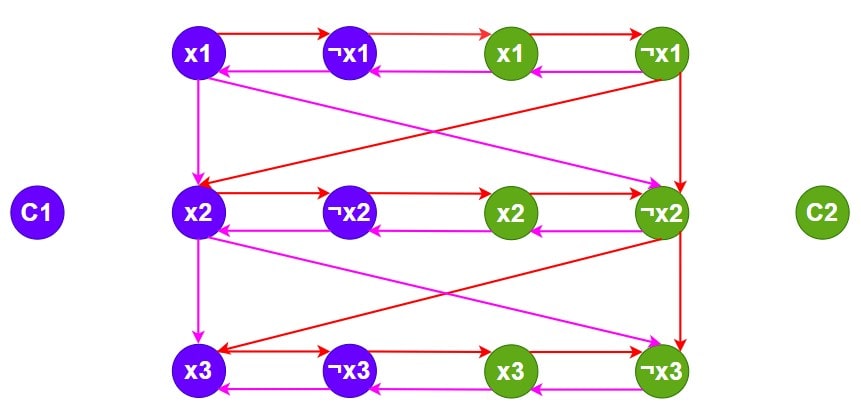
2. For each clause, create a pair of vertices representing the literal xi (true) and ¬xi​ (false). Also, create edges between xi to ¬xi and ¬xi to
3. Add two special vertices, Start and End, connected to the variables to form a cycle.

• • Connect the Start vertex to the first x1 vertex and the last ¬x1 vertex back to Start. Connect the first xn vertex to the End vertex​, and its last ¬xn vertex​, to the End
  • Finally, create an edge from End back to Start to complete the cycle.

4. For each clause
   • If a literal xi​ is present in a clause, add an edge from xi​ to the clause vertex and from the clause vertex back to ¬xi​.
   • If the clause contains ¬xi, connect ¬xi​ to the clause vertex and back from the clause vertex to xi​.
5. Verify the Hamiltonian Cycle

• • The constructed graph will contain a Hamiltonian cycle if and only if there exists a satisfying assignment for the original 3-SAT formula.
  • Check if the cycle formed in the graph includes all vertices without repeating any, indicating that the graph structure aligns with the required assignments.

.

Example

F = (¬x1 V x2 V ¬x3) Λ (x1 V ¬x2 V x3)

Step 1 – For each variable xi in the 3-SAT formula, create two nodes representing the literal xi (true) and ¬xi​ (false).

Step 2 – For two clauses, create two pair of nodes representing the literal xi (true) and ¬xi​ (false).

Step 3 – Add two vertices Start and End. Connect the two vertices as shown.

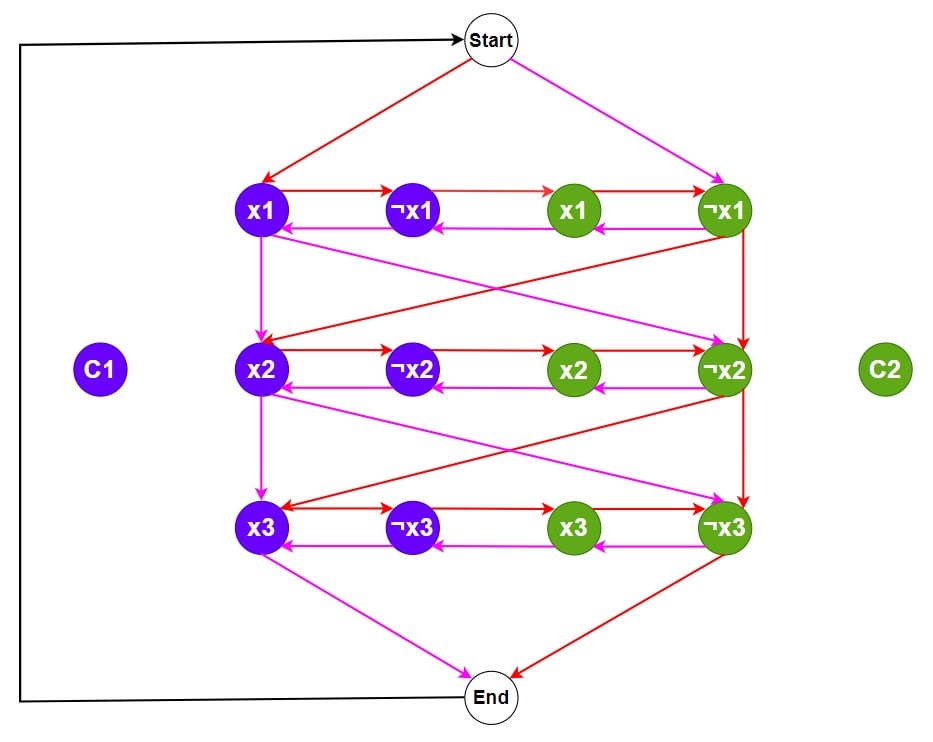
Step 4 – For each clause, C1 = (¬x1 V x2 V ¬x3) and C2 = (x1 V ¬x2 V x3), if a literal xi​ is present in a clause, add an edge from xi​ to the clause vertex and from the clause vertex back to ¬xi​ and vice-versa.

Here ¬x1 is present in the clause C1, so add an edge from ¬x1 to C1 and from C1 to x1. Likewise create the all edges.

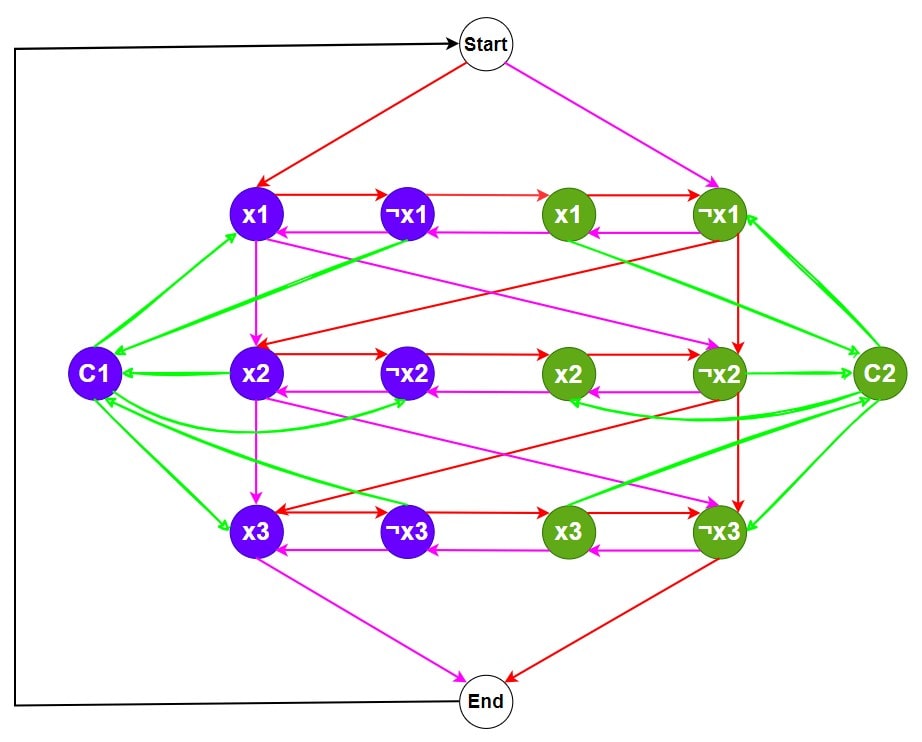
Step 4 – Verify the Hamiltonian Path or Cycle.

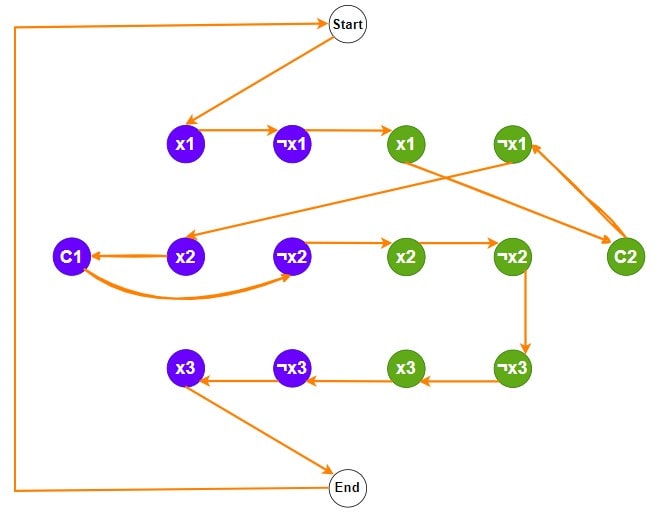
The Hamiltonian cycle exist in 3-SAT problem. Now to verify the solution Hamiltonian cycle into 3-SAT problem, we must look at the graph and find x1, x2 and x3.

So, x1 = true because the x1 line has left to right edges.

Also, x2 = true because the x2 line has left to right edges

Then, x3 = false because the x3 line has right to left edges.

F = (¬x1 V x2 V ¬x3) Λ (x1 V ¬x2 V x3)

F = (False V True V True) Λ (True V False V False)

F = True Λ True

F = True

Hence, 3-SAT Problem is true. it means that solving Hamiltonian Path Problem or Cycle Problem would allow us to solve 3-SAT as well.