Introduction
.
The Graph Colouring Problem is a classic problem in graph theory and computer science.
It involves assigning colours to the vertices of a graph such that no two adjacent vertices share the same color.
The primary objective is to minimize the number of colours used.
This problem is essential because it has numerous practical applications, including scheduling, register allocation in compilers, and frequency assignment in mobile networks.
.
Problem Statement
Input –
- A graph G = (V, E) where V is a set of vertices {v1, v2, …, vn} and E is a set of edges {e1, e2, …, em}.
- An integer M, representing the maximum number of colours available.
Constraints –
- Each vertex must be assigned exactly one color.
- No two adjacent vertices can have the same color.
- The number of colours used should be as minimum as possible.
Output –
- A colouring of the vertices such that no two adjacent vertices have the same color.
- The minimum number of colours used if possible, or a statement that the graph cannot be coloured with M colours.
.
Development of Graph Theory
In 1890, graph theory as a formal mathematical discipline began to develop, particularly with the work of Euler on the Seven Bridges of Königsberg problem. Graph theory provided a framework for understanding and formalizing the Graph Colouring Problem.
In 1950s, graph colouring was formally introduced as a problem in graph theory. Researchers like Claude Shannon began exploring its computational aspects. Shannon’s work on the colouring of communication networks laid the groundwork for understanding its practical applications.
In the 1970s, the Graph Colouring Problem gained significant attention with the development of computational complexity theory. The problem was shown to be NP-complete by Stephen Cook in his seminal paper on the theory of NP-completeness. This result indicated that no polynomial-time algorithm is known to solve all instances of the problem efficiently.
.
Chromatic Number
The chromatic number of a graph, often denoted by χ(G), is the minimum number of colours required to colour the vertices of the graph G, such that no two adjacent vertices share the same color.
.
Graph Colouring Decision Problem
The Graph Colouring Decision Problem is a specific type of problem in graph theory where the goal is to determine whether a given graph can be coloured using a specified number of colours such that no two adjacent vertices share the same color. This problem can be framed as a yes/no question.
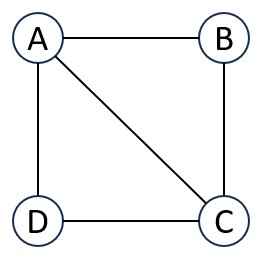
Consider a graph with 4 vertices and the following edges: (A-B), (A-C), (B-C), (A-D), (C-D).
.
Q – Given M = 2, Can we colour the graph with 2 colours?
Answer – No, due to the fact that in 2 colours, two neighbouring vertices are in the same color.
Q – Given M = 3, Can we color the graph with 3 colours?
Answer – Yes, we can color the vertices such that no two adjacent vertices share the same color.
.
Graph Colouring Optimization Problem
The Graph Colouring Optimization Problem is a more complex variation that seeks the minimum number of colours needed to color the graph while ensuring that no two adjacent vertices share the same color.
This problem focuses on finding the optimal solution, i.e., the smallest possible value of M that satisfies the colouring constraints.
With the given example in “graph colouring decision problem”, one can ask
Q – Find the minimum number of colours needed to color the graph or find the chromatic number of the graph.
Answer – The minimum number of colours needed is 3.
.
Back to the Graph Colouring Problem
One effective way to solve the Graph Colouring Problem is by using the backtracking algorithm.
Backtracking is a general algorithmic technique that incrementally builds candidates for the solution and abandons a candidate (“backtracks“) as soon as it determines that the candidate cannot possibly lead to a valid solution.
.
Backtracking Algorithm for Graph Colouring
- Start with the first vertex.
- Assign a color to the current vertex.
- Check if the assigned color is safe (i.e., it does not cause any two adjacent vertices to have the same color).
- Move to the next vertex.
- Repeat steps 2 and 3 until all vertices are coloured or no valid color can be assigned.
- Backtrack if no valid color is found for the current vertex and try the next color.
.
Example –
Consider the same graph as we were using in other problem also. We have 4 vertices and 3 colours (Red, Green, Blue)

- Start with the first vertex and colour it, Red.
- Then, second vertex, Green.
- Then, third vertex, Blue.
Make a backtracking tree
![]()
So, we got 6 solutions by backtracking approach.
Source code for Graph Colouring Problem
// COMPUTER GEEK – compgeek.co.in
// Write a program for Graph Colouring Problem by Backtracking
#include <stdio.h>
#include <stdbool.h>
#define MAX 100
// Function to print the color assignments
void printSolution(int color[], int V) {
printf(“Coloring of the vertices:\n”);
for (int i = 0; i < V; i++)
printf(“Vertex %d —> Color %d\n”, i + 1, color[i]);
}
// Function to check if the current color assignment is safe
bool isSafe(int v, int graph[MAX][MAX], int color[], int c, int V) {
for (int i = 0; i < V; i++)
if (graph[v][i] && c == color[i])
return false;
return true;
}
// A recursive utility function to solve the graph coloring problem
bool graphColoringUtil(int graph[MAX][MAX], int m, int color[], int v, int V) {
// Base case: If all vertices are assigned a color then return true
if (v == V)
return true;
// Consider this vertex v and try different colors
for (int c = 1; c <= m; c++) {
// Check if assignment of color c to v is fine
if (isSafe(v, graph, color, c, V)) {
color[v] = c;
// Recur to assign colors to the rest of the vertices
if (graphColoringUtil(graph, m, color, v + 1, V))
return true;
// If assigning color c doesn’t lead to a solution then remove it
color[v] = 0;
}
}
// If no color can be assigned to this vertex, then return false
return false;
}
// Function to solve the graph coloring problem
bool graphColoring(int graph[MAX][MAX], int m, int V) {
// Initialize all color values as 0 (no color is assigned yet)
int color[MAX] = {0};
// Start with the first vertex
if (graphColoringUtil(graph, m, color, 0, V) == false) {
printf(“Solution does not exist.\n”);
return false;
}
// Print the solution
printSolution(color, V);
return true;
}
int main() {
int V, m;
int graph[MAX][MAX];
// Input number of vertices
printf(“Enter the number of vertices: “);
scanf(“%d”, &V);
// Input the adjacency matrix of the graph
printf(“Enter the adjacency matrix of the graph (0 or 1):\n”);
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
scanf(“%d”, &graph[i][j]);
}
}
// Input the number of colors
printf(“Enter the number of colors: “);
scanf(“%d”, &m);
// Solve the graph coloring problem
graphColoring(graph, m, V);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Graph Colouring Problem by Backtracking
#include <iostream>
#define MAX 100
using namespace std;
// Function to print the color assignments
void printSolution(int color[], int V) {
cout << “Coloring of the vertices:\n”;
for (int i = 0; i < V; i++)
cout << “Vertex ” << i + 1 << ” —> Color ” << color[i] << endl;
}
// Function to check if the current color assignment is safe
bool isSafe(int v, int graph[MAX][MAX], int color[], int c, int V) {
for (int i = 0; i < V; i++)
if (graph[v][i] && c == color[i])
return false;
return true;
}
// A recursive utility function to solve the graph coloring problem
bool graphColoringUtil(int graph[MAX][MAX], int m, int color[], int v, int V) {
// Base case: If all vertices are assigned a color then return true
if (v == V)
return true;
// Consider this vertex v and try different colors
for (int c = 1; c <= m; c++) {
// Check if assignment of color c to v is fine
if (isSafe(v, graph, color, c, V)) {
color[v] = c;
// Recur to assign colors to the rest of the vertices
if (graphColoringUtil(graph, m, color, v + 1, V))
return true;
// If assigning color c doesn’t lead to a solution then remove it
color[v] = 0;
}
}
// If no color can be assigned to this vertex, then return false
return false;
}
// Function to solve the graph coloring problem
bool graphColoring(int graph[MAX][MAX], int m, int V) {
// Initialize all color values as 0 (no color is assigned yet)
int color[MAX] = {0};
// Start with the first vertex
if (graphColoringUtil(graph, m, color, 0, V) == false) {
cout << “Solution does not exist.\n”;
return false;
}
// Print the solution
printSolution(color, V);
return true;
}
int main() {
int V, m;
int graph[MAX][MAX];
// Input number of vertices
cout << “Enter the number of vertices: “;
cin >> V;
// Input the adjacency matrix of the graph
cout << “Enter the adjacency matrix of the graph (0 or 1):\n”;
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
cin >> graph[i][j];
}
}
// Input the number of colors
cout << “Enter the number of colors: “;
cin >> m;
// Solve the graph coloring problem
graphColoring(graph, m, V);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Graph Colouring Problem by Backtracking
import java.util.Scanner;
public class GraphColoring {
static final int MAX = 100;
// Function to print the color assignments
static void printSolution(int[] color, int V) {
System.out.println(“Coloring of the vertices:”);
for (int i = 0; i < V; i++)
System.out.println(“Vertex ” + (i + 1) + ” —> Color ” + color[i]);
}
// Function to check if the current color assignment is safe
static boolean isSafe(int v, int[][] graph, int[] color, int c, int V) {
for (int i = 0; i < V; i++)
if (graph[v][i] == 1 && c == color[i])
return false;
return true;
}
// A recursive utility function to solve the graph coloring problem
static boolean graphColoringUtil(int[][] graph, int m, int[] color, int v, int V) {
// Base case: If all vertices are assigned a color then return true
if (v == V)
return true;
// Consider this vertex v and try different colors
for (int c = 1; c <= m; c++) {
// Check if assignment of color c to v is fine
if (isSafe(v, graph, color, c, V)) {
color[v] = c;
// Recur to assign colors to the rest of the vertices
if (graphColoringUtil(graph, m, color, v + 1, V))
return true;
// If assigning color c doesn’t lead to a solution then remove it
color[v] = 0;
}
}
// If no color can be assigned to this vertex, then return false
return false;
}
// Function to solve the graph coloring problem
static boolean graphColoring(int[][] graph, int m, int V) {
// Initialize all color values as 0 (no color is assigned yet)
int[] color = new int[V];
// Start with the first vertex
if (!graphColoringUtil(graph, m, color, 0, V)) {
System.out.println(“Solution does not exist.”);
return false;
}
// Print the solution
printSolution(color, V);
return true;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// Input number of vertices
System.out.print(“Enter the number of vertices: “);
int V = scanner.nextInt();
int[][] graph = new int[MAX][MAX];
// Input the adjacency matrix of the graph
System.out.println(“Enter the adjacency matrix of the graph (0 or 1):”);
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
graph[i][j] = scanner.nextInt();
}
}
// Input the number of colors
System.out.print(“Enter the number of colors: “);
int m = scanner.nextInt();
// Solve the graph coloring problem
graphColoring(graph, m, V);
scanner.close();
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for Graph Colouring Problem by Backtracking
def printSolution(color, V):
print(“Coloring of the vertices:”)
for i in range(V):
print(f”Vertex {i + 1} —> Color {color[i]}”)
def isSafe(v, graph, color, c, V):
for i in range(V):
if graph[v][i] == 1 and color[i] == c:
return False
return True
def graphColoringUtil(graph, m, color, v, V):
if v == V:
return True
for c in range(1, m + 1):
if isSafe(v, graph, color, c, V):
color[v] = c
if graphColoringUtil(graph, m, color, v + 1, V):
return True
color[v] = 0
return False
def graphColoring(graph, m, V):
color = [0] * V
if not graphColoringUtil(graph, m, color, 0, V):
print(“Solution does not exist.”)
return False
printSolution(color, V)
return True
if __name__ == “__main__”:
V = int(input(“Enter the number of vertices: “))
graph = []
print(“Enter the adjacency matrix of the graph (0 or 1):”)
for i in range(V):
row = list(map(int, input().split()))
graph.append(row)
m = int(input(“Enter the number of colors: “))
graphColoring(graph, m, V)
Enter the number of vertices: 4
Enter the adjacency matrix of the graph (0 or 1):
0 1 1 1
1 0 1 0
1 1 0 1
1 0 1 0
Enter the number of colours: 3
Colouring of the vertices:
Vertex 1 —> Color 1
Vertex 2 —> Color 2
Vertex 3 —> Color 3
Vertex 4 —> Color 2
=== Code Execution Successful ===
Region Colouring Map Algorithm
Region Colouring in Maps refers to the practice of assigning different colours to various regions (such as countries, states, or provinces) on a map in such a way that no two adjacent regions share the same color. This concept is directly related to the Graph Colouring Problem in computer science, where each region is represented as a vertex in a graph, and edges exist between vertices that correspond to adjacent regions on the map.
.
Definition
In a Region Colouring Map problem
- Regions – Represented as vertices in a graph.
- Borders – The shared boundaries between regions are represented as edges between the corresponding vertices.
- Colouring – Assigning a color to each region (vertex) such that no two adjacent regions (connected vertices) have the same color.
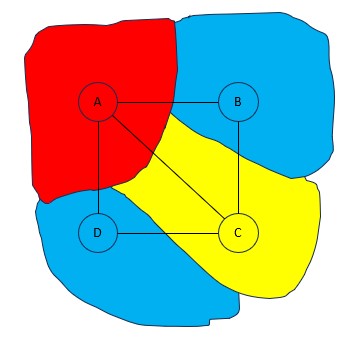
A region is connected to B region,
B region is connected to C region,
A region is connected to C region,
D region is connected to C region,
A region is connected to D region, but
B region is not connected to D region, as they have no edges in between them.
.
The most popular algorithm for region colouring, particularly in map colouring, is the Four-Color Theorem, which states that any planar map (a map that can be drawn on a flat surface without any regions overlapping) can be coloured with no more than four colours.
.
Time Complexity of Graph Colouring Algorithm
It is determined by the number of recursive calls made during the algorithm’s execution. V as the number of vertices (or regions) in the graph and m as the number of colours available. In the worst case, the algorithm tries all possible ways to color the graph,
Therefore, the worst-case time complexity of the Graph Colouring Algorithm using backtracking is O(m^V).
.
Space Complexity of Graph Colouring Algorithm
The space complexity of the Graph Colouring algorithm using backtracking can be analyzed based on the space required for a graph with V vertices and E edges, the adjacency list requires O(V+E) space.
Color array stores the color assigned to each vertex. It has a size of V, so it requires O(V) space.
The depth of the recursive call stack is equal to the number of vertices V, since each vertex is processed in a separate recursive call. Thus, the space required for the call stack is O(V).
Total Space Complexity = O(V+E) + O(V) + O(V) = O(V+E)
.
Advantages of the Graph Colouring Algorithm
- The algorithm is straightforward to understand and implement. It uses a recursive approach to explore all possible colourings of the graph.
- The backtracking algorithm guarantees finding an exact solution if one exists.
- The algorithm can be adapted to various types of graph-related problems such as scheduling problems or register allocation in compilers.
- Backtracking can be applied to any graph structure, regardless of the graph’s nature, whether it is sparse, dense, or has other special properties.
.
Disadvantages of the Graph Colouring Algorithm
- The backtracking algorithm has an exponential time complexity in the worst case, typically O(mV), where m is the number of colours and V is the number of vertices. This makes it impractical for large graphs or graphs with many vertices.
- Due to its exhaustive nature, the backtracking approach becomes infeasible for large graphs or graphs with high connectivity, as it may require an enormous amount of computation time.
- The algorithm requires additional memory for storing the recursive call stack, which can become significant for large graphs, leading to high space complexity.
- The algorithm does not scale well with the increase in graph size, limiting its practical use in real-world large-scale problems.
.
Applications of the Graph Colouring Algorithm
- Used in cartography to color regions on a map so that no two adjacent regions share the same color. This helps in visual distinction between neighbouring regions.
- Applied in scheduling tasks or exams where certain tasks/exams (represented as vertices) cannot occur simultaneously (connected by edges).
- In compiler design, graph colouring is used for register allocation. Variables that interfere with each other are assigned to different registers, analogous to colouring graph vertices.
- Used in telecommunications to assign frequencies to radio stations or cell towers such that no two stations/towers with overlapping ranges use the same frequency.
- Certain puzzles and games, such as Sudoku, can be modelled as a graph colouring problem where each cell must be assigned a value (color) based on specific rules.
- In various operations research problems, graph colouring helps in allocating limited resources (like machines or crews) to tasks that cannot be done simultaneously.
Test Yourself
Q1- Why is the backtracking algorithm used for solving the Graph Colouring Problem, and what are its main steps?
The backtracking algorithm is used for solving the Graph Colouring Problem because it systematically explores all possible colourings and backtracks when a colouring does not meet the constraints. Its main steps are:
- Assign a colour to the current vertex.
- Check if this colour assignment is safe (i.e., no adjacent vertex has the same colour).
- Move to the next vertex and repeat the process.
- If a valid colour cannot be assigned, backtrack to try different colour options.
Q2- What is the chromatic number of a graph, and how does it relate to the Graph Colouring Problem?
The chromatic number of a graph is the minimum number of colours required to colour the vertices such that no two adjacent vertices share the same colour.
It directly relates to the Graph Colouring Problem as the problem’s objective is to find this minimum number of colours.
Q3- How does the time complexity of the backtracking algorithm for graph colouring compare with its space complexity?
The time complexity of the backtracking algorithm for graph colouring is O(m^V), where m is the number of colours and V is the number of vertices.
This is due to the exhaustive nature of exploring all possible colour assignments.
The space complexity is O(V + E) for storing the adjacency matrix and colour array, plus O(V) for the recursive call stack, resulting in a total space complexity of O(V + E).
Q4- In what scenarios might the backtracking algorithm for graph colouring become impractical?
The backtracking algorithm becomes impractical for large graphs or graphs with high connectivity due to its exponential time complexity.
The extensive computation required to explore all possible colourings makes it infeasible for very large graphs or when there are many vertices.
Q5- Discuss the advantages and disadvantages of using the backtracking algorithm for the Graph Colouring Problem.
Advantages
- Simple and easy to implement.
- Guarantees finding an exact solution if one exists.
- Adaptable to various graph-related problems.
Disadvantages
- Exponential time complexity, making it impractical for large graphs.
- High space complexity due to the recursive call stack.
- Inefficient for graphs with high connectivity or large sizes.
Q6- What is the main objective of the Graph Colouring Problem?
To find the shortest path in a graph.
To assign colours to the vertices such that no two adjacent vertices share the same colour.
To find the maximum flow in a network.
To calculate the graph’s diameter
Ans – (2)
Explanation – The main objective is to ensure that adjacent vertices do not share the same colour while using the minimum number of colours.
Q7- In the Graph Colouring Decision Problem, what is the nature of the question asked?
Find the minimum number of colours needed
Determine if a given graph can be coloured with a specified number of colours
Calculate the chromatic number of the graph
Identify all possible colourings of the graph
Ans – (2)
Explanation – The Graph Colouring Decision Problem asks whether it is possible to colour the graph with a given number of colours while satisfying the constraints.
Q8- In a graph colouring algorithm, what does the term “chromatic number” refer to?
The maximum number of colours needed
The minimum number of colours needed
The total number of vertices
The number of edges in the graph
Ans – (2)
Explanation – The chromatic number is the smallest number of colours required to colour the graph so that no two adjacent vertices have the same colour.
Q9- Which type of problem does the Graph Colouring Optimization Problem focus on?
Finding a path in the graph
Checking if a graph can be coloured with a given number of colours
Counting the number of valid colourings
Finding the minimum number of colours required for valid colouring
Ans – (4)
Explanation – The Graph Colouring Optimization Problem seeks to determine the smallest number of colours needed to colour the graph correctly.
Q10- In the context of the backtracking algorithm, what does the term “safe” mean when assigning a colour to a vertex?
The colour is not used by any other vertex
The colour does not cause a constraint violation with adjacent vertices
The colour is the most frequently used
The colour is randomly chosen
Ans – (2)
Explanation – A colour assignment is considered “safe” if it does not violate the condition that adjacent vertices must have different colours.
Q11- Which of the following real-world applications can be modelled as a Graph Colouring Problem?
Routing data in a network
Assigning time slots for exams
Sorting data in a database
Encrypting data
Ans – (2)
Explanation – Graph colouring can be applied to scheduling problems where tasks or exams that cannot overlap are represented as vertices, and the goal is to assign time slots (colours) so that no conflicting tasks share the same slot.






