SYLLABUS
Discrete Mathematics: Propositional and first order logic. Sets, relations, functions, partial orders and lattices. Monoids, Groups. Graphs: connectivity, matching, coloring. Combinatorics: counting, recurrence relations, generating functions. Linear Algebra: Matrices, determinants, system of linear equations, eigenvalues and eigenvectors, LU decomposition. Calculus: Limits, continuity and differentiability. Maxima and minima. Mean value theorem. Integration. Probability and Statistics: Random variables. Uniform, normal, exponential, poisson and binomial distributions. Mean, median, mode and standard deviation. Conditional probability and Bayes theorem
Q1 – Let 𝑓:ℝ → ℝ be a function such that 𝑓(𝑥) = max{𝑥, 𝑥3}, 𝑥∈ℝ , where ℝ is the set of all real numbers. The set of all points where 𝑓(𝑥) is NOT differentiable is
(A) {−1,1,2}
(B) {−2,−1,1}
(C) {0,1}
(D) {−1,0,1}
Ans – (D)
Explanation – Function f(x) = max{x, x3}
The points where it is not differentiable is that, the function is not continuous at those points.
If x is max, then x ≥ x3
So, x – x3 ≥ 0
ð x(1 – x2) ≥ 0
ð x = 0 | 1 – x2 = 0
ð x = 0 | x2 = 1
ð x = 0 | x = 1 | x = -1
If x3 is max, then x3 ≥ x
So, x3 – x ≥ 0
ð x(x2 – 1) ≥ 0
ð x = 0 | x2 = 1
ð x = 0 | x = -1 | x = 1
To check whether it is differentiable or not, we can compute the derivative
F(x) = { x3, if x ≥ 1 So, F’(x) = 3x2
F(x) = ( x, if 0 ≤ x < 1 So, F’(x) = 1
F(x) = { x3, if -1 ≤ x < 0 So, F’(x) = 3x2
F(x) = { x, if -1 < x So, F’(x) = 1
Means the point where x = -1, 0 and 1, the function is not continuous. Hence option (D) is the answer.
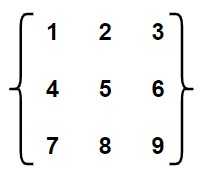
Q2 – The product of all eigenvalues of the matrix is
(A) −1
(B) 0
(C) 1
(D) 2
Ans – (B)
Explanation – An eigenvalue is a special number related to a square matrix that provides insight into the geometry of a square matrix. If you are given an n×n matrix A, any eigenvalue λ can be found based on the characteristic equation. det(A − λI) = 0.
Matrix = 1(5*9 – 6*8) – 2(4*9 – 6*7) + 3(4*8 – 5*7)
Matrix = -3 – 2(-6) + 3(-3) = -3 + 12 – 9 = 0
Considering the determinant of the matrix you submitted, it is 0 because one of the eigenvalues is equal to zero, consequently it indicates that the product of each eigenvalue is also equal to zero. Therefore, the correct response to your question is (B) = 0.
Q3 – Consider a permutation sampled uniformly at random from the set of all permutations of {1, 2, 3, ⋯, 𝑛} for some 𝑛 ≥ 4. Let 𝑋 be the event that 1 occurs before 2 in the permutation, and 𝑌 the event that 3 occurs before 4. Which one of the following statements is TRUE?
(A) The events 𝑋 and 𝑌 are mutually exclusive
(B) The events 𝑋 and 𝑌 are independent
(C) Either event 𝑋 or 𝑌 must occur
(D) Event 𝑋 is more likely than event 𝑌
Ans – (B)
Explanation – 𝑋 be the event that 1 occurs before 2, and
𝑌 the event that 3 occurs before 4.
The X and Y are not relating to each other.
Probability of X event (1 appear before 2) = ½
Probability of Y event (3 appear before 4) = ½
Checking the Provided Options
(A) The events X and Y are mutually exclusive → False
For two events to be mutually exclusive, they cannot occur at the same time. But, both of these could occur at the same time, as seen in the permutation 1,3,2,4,5,…., so these two could not be mutually exclusive.
(B) The events X and Y are independent → True
We have proved this from a mathematical standpoint, therefore this answer is true.
(C) Either event X or event Y must occur → False
This could be exemplified by the permutation 2,1,4,3,5,… where both events X and Y do not occur. Thus this would be false.
(D) Event X is more likely than event Y → False
Both event X and event Y have the same probability; therefore, this statement would not hold true.
Q4 – Let 𝐴 and 𝐵 be two events in a probability space with 𝑃(𝐴) = 0.3, 𝑃(𝐵) = 0.5, and 𝑃(𝐴∩𝐵) = 0.1. Which of the following statements is/are TRUE?
(A) The two events 𝐴 and 𝐵 are independent
(B) 𝑃(𝐴 ∪ 𝐵) = 0.7
(C) 𝑃(𝐴 ∩ 𝐵C ) = 0.2, where 𝐵C is the complement of the event 𝐵
(D) 𝑃(𝐴C ∩ 𝐵C) = 0.4, where 𝐴C and 𝐵C are the complements of the events 𝐴 and 𝐵, respectively
Ans – (B, C)
Explanation –
We have the probabilities of two events, P(A)=0.3, P(B)=0.5, and the intersection P(A∩B)=0.1.
Option (A), for A and B to be independent, we must have P(A∩B) = P(A) ⋅ P(B). However, 0.3 ⋅ 0.5 = 0.15 is not equal to the provided P(A∩B) of 0.1. Therefore, A and B are not independent, and so (A) is false.
Option (B), if the union A ∪ B is equal to 0.7. We calculate the union using the formula P(A∪B) = P(A) + P(B) − P(A∩B) which gives us P(A∪B) = 0.3 + 0.5 − 0.1 = 0.7 which means (B) is true.
Next, let’s consider option (C) which describes P(A∩BC ) = 0.2. This means the probability that A occurs but B does not. To calculate this, we can use P(A) − P(A∩B), which allows us to find P(A∩BC) = 0.3 − 0.1 = 0.2, therefore (C) is true.
Finally, let’s examine the last option (D) which refers to the event AC∩BC = 0.4 which is the probability that neither A occurs nor B. This is equal to 1 − P(A∪B), which is equal to 1 − 0.7 = 0.3. Therefore, D is false.
Q5 – Let 𝐴 and 𝐵 be non-empty finite sets such that there exist one-to-one and onto functions (i) from 𝐴 to 𝐵 and (ii) from 𝐴 × 𝐴 to 𝐴 ∪ 𝐵. The number of possible values of |𝐴| is __________
Ans – (2)
Explanation – Let ∣A∣ = n, and there exists a bijection (one-to-one and onto function) from A → B. So, ∣A∣ = ∣B∣ and ∣B∣ = n
Also, ∣A × A∣ = n × n = n2
And, ∣A ∪ B∣ ≤ 2n|
From the bijection A × A → A ∪ B,
we get n2 ≤ 2n
- n (n−2) ≤ 0
- n = 0 this is not right as A and B are non-empty sets
- n = 2, this is correct.
So, the number of possible values of |𝐴| is 2.
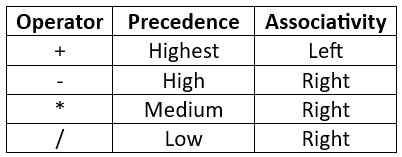
Q6 – Consider the operator precedence and associativity rules for the integer arithmetic operators given in the table below.
The value of the expression 3+1+5∗2/7+2−4−7−6/2 as per the above rules is __________
Ans – (6)
Explanation – We take the highest precedence first, and put the parentheses with the associativity.
- 3+1+5∗2 / 7+2−4−7−6 / 2
- ((3 + 1) + 5) * 2 / (7 + 2) – 4 – 7 – 6 / 2 [ + has highest precedence]
- ((3 + 1) + 5) * 2 / ((7 + 2) – (4 – (7 – 6))) / 2 [ – has high precedence]
- (((3 + 1) + 5) * 2) / ((7 + 2) – (4 – (7 – 6))) / 2 [ * has medium precedence]
- ((((3 + 1) + 5) * 2) / (((7 + 2) – (4 – (7 – 6))) / 2)) [ / has low precedence]
- (((4 + 5) * 2) / ((9 – (4 – (7 – 6))) / 2))
- ((9 * 2) / ((9 – ( 4 – 1)) / 2))
- (18 / ((9 – 3) / 2))
- (18 / (6 / 2))
- (18 / 3) = 6 Ans.
Q7 – Let 𝐴 be any 𝑛 × 𝑚 matrix, where 𝑚 >𝑛. Which of the following statements is/are TRUE about the system of linear equations 𝐴𝑥=0 ?
(A) There exist at least 𝑚−𝑛 linearly independent solutions to this system
(B) There exist 𝑚−𝑛 linearly independent vectors such that every solution is a linear combination of these vectors
(C) There exists a non-zero solution in which at least 𝑚−𝑛 variables are 0
(D) There exists a solution in which at least 𝑛 variables are non-zero
Ans – (A)
Explanation – Assume that A is an n × m matrix where m > n. This implies that A has m variables (because each column corresponds to a variable in the equation Ax = 0). This means we only have n equations (because there are n rows). You have more variables than equations.
For example, you could think of 3 equations and 5 variables. Is it possible to find the solution for 5 unknowns using only 3 equations? No! Thus, at least m−n variables can be chosen freely. So, in option (A) there will be at least m−n linearly independent solutions to this system!
Q8 – A bag contains 10 red balls and 15 blue balls. Two balls are drawn randomly without replacement. Given that the first ball drawn is red, the probability (rounded off to 3 decimal places) that both balls drawn are red is _________.
Ans – (0.370 to 0.380)
Explanation – There are 25 balls of which 10 are red balls and 15 are blue balls. Two balls are drawn randomly without replacement.
The first one is red, so there are 24 balls of which 9 are red balls and 15 are blue balls
Probability = 9/24 = 0.375.
So, 0.375 is exactly between 0.370 to 0.380.