SYLLABUS
Programming in Python, basic data structures: stacks, queues, linked lists, trees, hash tables; Search algorithms: linear search and binary search, basic sorting algorithms: selection sort, bubble sort and insertion sort; divide and conquer: mergesort, quicksort; introduction to graph theory; basic graph algorithms: traversals and shortest path.
Q1 – Consider performing depth-first search (DFS) on an undirected and unweighted graph G starting at vertex 𝑠. For any vertex 𝑢 in G, 𝑑[𝑢] is the length of the shortest path from 𝑠 to 𝑢. Let (𝑢,𝑣) be an edge in G such that 𝑑[𝑢]<𝑑[𝑣]. If the edge (𝑢,𝑣) is explored first in the direction from 𝑢 to 𝑣 during the above DFS, then (𝑢,𝑣) becomes a ______ edge.
(A) tree
(B) cross
(C) back
(D) gray
(GATE DS&AI 2024)
Ans – (A)
Explanation – Now let us look at the question where we are given that d[u] < d[v], which means vertex u is nearer to the source vertex s than vertex v is. If we explore the edge (u,v) first from u to v during DFS, it means that v has not yet been visited. Hence this edge will be tree edge as it is first discovery of new vertex. Therefore, the answer is tree and it matches with option (A).
Q2 – Match the items in Column 1 with the items in Column 2 in the following table:
Column 1
(p) First In First Out
(q) Lookup Operation
(r) Last In First Out
Column 2
(i) Stacks
(ii) Queues
(iii) Hash Tables
(A) (p) − (ii), (q) − (iii), (r) − (i)
(B) (p) − (ii), (q) − (i), (r) − (iii)
(C) (p) − (i), (q) − (ii), (r) − (iii)
(D) (p) − (i), (q) − (iii), (r) − (ii)
(GATE DS&AI 2024)
Ans – (A)
Explanation – Stacks are one of the most uncomplicated types of data structures which are those that store items in a particular order — Last In, First Out (LIFO).
Queue is a linear data structure that is the simplest, least sophisticated data structure in computer science, sometimes allowing only one piece of data in it. The First In, First Out (FIFO) rule must be followed.
Hash Tables – A hash table is a data-like structure mainly composed of a key-value pair and which is quite helpful for storing the data. Its main advantage is that the hash function locates the query data immediately. The fast lookup, insertion, and deletion operations can be completed with no more than O(1) time complexity on the average, which is the main feature of the hash table.
Q3 – Consider performing uniform hashing on an open address hash table with load factor 𝛼 = 𝑛/𝑚 < 1, where 𝑛 elements are stored in the table with 𝑚 slots. The expected number of probes in an unsuccessful search is at most 1/(1−𝛼) .
Inserting an element in this hash table requires at most ______ probes, on average.
(A) ln(1/(1−𝛼))
(B) 1/1−𝛼
(C) 1 + 𝛼/2
(D) 1/(1+𝛼)
(GATE DS&AI 2024)
Ans – (B)
Explanation – We use a hash table with open addressing in data structure. With this system, we have a table with m slots (positions to keep the items), also we have n elements stored. The load factor is α = n/m, which shows how much of the table is full. Because α < 1, the table is not filled up yet.
When we want to add a new element. We go to the place where the hash function sends us first. If it is full, we go to the next position. We look for a slot where we can insert the new element, by trying one by one slot. This is a search that ends unsuccessfully because we are looking for an unoccupied slot.
In the situation of equal probability for all empty slots (i.e. uniform hashing), the expected number of probes in an unsuccessful search is 1/(1−α). As insertion is an unsuccessful search (you stop at an empty cell), the average number of probes for insertion is also 1/(1−α).
Q4 – Consider the following tree traversals on a full binary tree:
(i) Preorder
(ii) Inorder
(iii) Postorder
Which of the following traversal options is/are sufficient to uniquely reconstruct the full binary tree?
(A) (i) and (ii)
(B) (ii) and (iii)
(C) (i) and (iii)
(D) (ii) only
(GATE DS&AI 2024)
Ans – (A, B, C)
Explanation – We have three tree traversals technique on a binary tree. Basically, if we are given an inorder traversal of binary tree and a preorder or postorder traversal of a binary tree, then we can uniquely draw the diagram of such binary tree. Only two are necessary to create a diagram uniquely (Inorder – Preorder) or (Inorder – Postorder).
But in the question, we make a full binary tree, then preorder traversal and postorder traversal alone are sufficient to create the tree uniquely.
Q5 – Consider sorting the following array of integers in ascending order using an in-place Quicksort algorithm that uses the last element as the pivot.
60 | 70 | 80 | 90 | 100 |
The minimum number of swaps performed during this Quicksort is ______.
(GATE DS&AI 2024)
Ans – (0)
Explanation –
The array is already sorted but we have to perform quick sort algorithm that the swap happens or not.
Quick Sort
Partitioning Using Nico Lomuto Scheme Algorithm
function partition(array, low, high)
pi = array[high] // Choose last element as pivot (pi)
i = low – 1 // Maintain index i to separate elements from larger ones.
for j = low to high – 1 // Traverse the array
if array[j] <= pivot
i = i + 1
swap array[i] with array[j]
// Swap smaller elements before the pivot
swap array[i + 1] with array[high]
return i + 1
There would be no number swapped in the original array, so number of swaps would be 0.
Q6 – The fundamental operations in a double-ended queue D are:
insertFirst(e) – Insert a new element e at the beginning of D.
insertLast(e) – Insert a new element e at the end of D.
removeFirst() – Remove and return the first element of D.
removeLast() – Remove and return the last element of D.
In an empty double-ended queue, the following operations are performed:
insertFirst(10)
insertLast(32)
a ←removeFirst()
insertLast(28)
insertLast(17)
a ←removeFirst()
a ← removeLast()
The value of a is ______.
(GATE DS&AI 2024)
Ans – (17)
Explanation – The double ended queue D = [ ]
Step 1 – insertFirst(10), D = [10]
Step 2 – insertLast(32), D = [10, 32]
Step 3 – a ←removeFirst(), D = [32], a = 10
Step 4 – insertlast(28), D = [32, 28]
Step 5 – insertlast(17), D = [32, 28, 17]
Step 6 – a ←removeFirst(), D = [28, 17], a = 32
Step 7 – a ← removeLast(), D = [28], a = 17
The value of a is 17.
Q7 – Consider the following Python code:
def count(child_dict, i):
if i not in child_dict.keys():
return 1
ans = 1
for j in child_dict[i]:
ans += count(child_dict, j)
return ans
child_dict = dict()
child_dict[0] = [1, 2]
child_dict[1] = [3, 4, 5]
child_dict[2] = [6, 7, 8]
print(count(child_dict,0))
Which ONE of the following is the output of this code?
(A) 6
(B) 1
(C) 8
(D) 9
(GATE DS&AI 2024)
Ans – (D)
Explanation – The code counts the total number of nodes from node 0 through the use of a dictionary called child_dict to indicate the tree structure.
Start with 0 → count = 1
Go to 1
count = 1 for [1] + 1 for [3] + 1 for [4] + 1 for [5] = 4
Go to 2
count = 1 for [2] + 1 for [6] + 1 for [7] + 1 for [8] = 4
Now total count = 1 (for 0) + 4 (from 1 left subtree) + 4 (from 2 right subtree) = 9
Q8 – Consider the function computeS(X) whose pseudocode is given below:
computeS(X)
𝑆[1]←1
for 𝑖 ←2 to 𝑙𝑒𝑛𝑔𝑡ℎ(𝑋)
𝑆[𝑖]←1
if 𝑋[𝑖−1]≤𝑋[𝑖]
𝑆[𝑖]←𝑆[𝑖]+𝑆[𝑖−1]
end if
end for
return S
Which ONE of the following values is returned by the function computeS(X) for X = [6, 3, 5, 4, 10]?
(A) [1, 1, 2, 3, 4]
(B) [1, 1, 2, 3, 3]
(C) [1, 1, 2, 1, 2]
(D) [1, 1, 2, 1, 5]
(GATE DS&AI 2024)
Ans – (C)
Explanation – X = [6, 3, 5, 4, 10]
Dry run –
S[1] ← 1
So, S = [1, _, _, _, _]
for 𝑖 ←2 to 𝑙𝑒𝑛𝑔𝑡ℎ(𝑋)
i = 2
- X[1] = 6, X[2] = 3
- 6 ≤ 3 is false, so
- S[2] = 1
- S = [1, 1, _, _, _]
i = 3
- X[2] = 3, X[3] = 5
- 3 ≤ 5 is true, so
- S[3] = 1 + S[2] = 1 + 1 = 2
- S = [1, 1, 2, _, _]
i = 4
- X[3] = 5, X[4] = 4
- 5 ≤ 4 is false, so
- S[4] = 1
- S = [1, 1, 2, 1, _]
i = 5
- X[4] = 4, X[5] = 10
- 4 ≤ 10 is true, so
- S[5] = 1 + S[4] = 1 + 1 = 2
- S = [1, 1, 2, 1, 2]
Hence option C is the answer.
Q9 – Let 𝐹(𝑛) denote the maximum number of comparisons made while searching for an entry in a sorted array of size 𝑛 using binary search.
Which ONE of the following options is TRUE?
(A) 𝐹(𝑛)=𝐹(⌊𝑛/2⌋)+1
(B) 𝐹(𝑛)=𝐹(⌊𝑛/2⌋)+𝐹(⌈𝑛/2⌉)
(C) 𝐹(𝑛)=𝐹(⌊𝑛/2⌋)
(D) 𝐹(𝑛)=𝐹(𝑛−1)+1
(GATE DS&AI 2024)
Ans – (A)
Explanation – For an array of size n, the largest number of comparisons that can be done (in the worst-case scenario).
1. It picks the middle with 1 comparison.
2. Then it looks for one half, of size ⌊n/2⌋ (or smaller).
So, option A is the answer.
Q10 – Consider the following Python function:
def fun(D, s1, s2):
if s1 < s2:
D[s1], D[s2] = D[s2], D[s1]
fun(D, s1+1, s2-1)
What does this Python function fun() do? Select the ONE appropriate option below.
(A) It finds the smallest element in D from index s1 to s2, both inclusive.
(B) It performs a merge sort in-place on this list D between indices s1 and s2, both inclusive.
(C) It reverses the list D between indices s1 and s2, both inclusive.
(D) It swaps the elements in D at indices s1 and s2, and leaves the remaining elements unchanged.
(GATE DS&AI 2024)
Ans – (C)
Explanation – The function checks if s1 < s2. If true,
- It swaps elements at positions s1 and s2.
- Then it calls itself recursively with s1+1 and s2-1.
This continues until s1 >= s2, which is the stopping condition.
This is a classic in-place reversal of the list segment from s1 to s2. It swaps the first and last, then the second and second-last, and so on.
Let’s say D = [37, 49, 78, 61]
fun(D, 0, 3)
- Swap D[0] and D[3] → swap 37 and 61
- List becomes: [61, 49, 78, 37]
- Recursive call: fun(D, 1, 2)
fun(D, 1, 2)
- Swap D[1] and D[2] → swap 49 and 78
- List becomes: [61, 78, 49, 37]
- Recursive call: fun(D, 2, 1)
fun(D, 2, 1)
- s1 < s2 is false → recursion stops.
The list has been reversed [61, 78, 49, 37] from index 0 to 3 (inclusive).
Q11 – Consider a state space where the start state is number 1. The successor function for the state numbered n returns two states numbered n+1 and n+2. Assume that the states in the unexpanded state list are expanded in the ascending order of numbers and the previously expanded states are not added to the unexpanded state list.
Which ONE of the following statements about breadth-first search (BFS) and depth-first search (DFS) is true, when reaching the goal state number 6?
(A) BFS expands more states than DFS.
(B) DFS expands more states than BFS.
(C) Both BFS and DFS expand equal number of states.
(D) Both BFS and DFS do not reach the goal state number 6.
(GATE DS&AI 2024)
Ans – (C)
Explanation – We have to start with state number 1.
The successor function for the state numbered n returns two states numbered n+1 and n+2.
Means if the successor function for 1, returns 2 and 3.
The states in the unexpanded state list are expanded in the ascending order of numbers that is 1, 2, 3, 4,…
The previously expanded states are not added to the unexpanded state list.
In BFS, it is expanded, level by level, but in DFS, goes deep inside the path and then backtrack if needed.

Hence, the option (C) is the correct answer.
Q12 – Consider the following sorting algorithms:
(i) Bubble sort
(ii) Insertion sort
(iii) Selection sort
Which ONE among the following choices of sorting algorithms sorts the numbers in the array [4, 3, 2, 1, 5] in increasing order after exactly two passes over the array?
(A) (i) only
(B) (iii) only
(C) (i) and (iii) only
(D) (ii) and (iii) only
(GATE DS&AI 2024)
Ans – (B)
Explanation –
Bubble Sort
Input – [4, 3, 2, 1, 5]
Pass 1st – [3, 2, 1, 4, 5]
Pass 2nd – [2, 1, 3, 4, 5]
Not sorted in increasing order.
You can check here – https://compgeek.co.in/bubble-sort/
Insertion Sort
Input – [4, 3, 2, 1, 5]
Pass 1st – [4 sorted | unsorted 3, 2, 1, 5]
Pass 2nd – [3, 4 sorted | unsorted 2, 1, 5]
Not sorted in increasing order.
You can check here – https://compgeek.co.in/insertion-sort/
Selection Sort
Input – [4, 3, 2, 1, 5]
Pass 1st – [1, 3, 2, 4, 5]
Pass 2nd – [1, 2, 3, 4, 5]
It is sorted in increasing order.
You can check here – https://compgeek.co.in/selection-sort/
Q13 – Consider the directed acyclic graph (DAG) below:

Which of the following is/are valid vertex orderings that can be obtained from a topological sort of the DAG?
(A) P Q R S T U V
(B) P R Q V S U T
(C) P Q R S V U T
(D) P R Q S V T U
(GATE DS&AI 2024)
Ans – (B, D)
Explanation – Any topological sort must satisfy the following
- P and R before Q
- Q before S and V
- S before U
- V before T
Option (B) and (D) are correct because it follows above rules.
Q14 – Let H, 𝐼, 𝐿, and 𝑁 represent height, number of internal nodes, number of leaf nodes, and the total number of nodes respectively in a rooted binary tree.
Which of the following statements is/are always TRUE?
(A) 𝐿 ≤ 𝐼 + 1
(B) 𝐻+1 ≤ 𝑁 ≤ 2𝐻+1 −1
(C) 𝐻 ≤ 𝐼 ≤ 2𝐻 −1
(D) 𝐻 ≤ 𝐿 ≤ 2𝐻 −1
(GATE DS&AI 2024)
Ans – (A, B, C)
Explanation – Height = H
Number of Internal nodes = I
Number of Leaf nodes = L
Total number of nodes = N
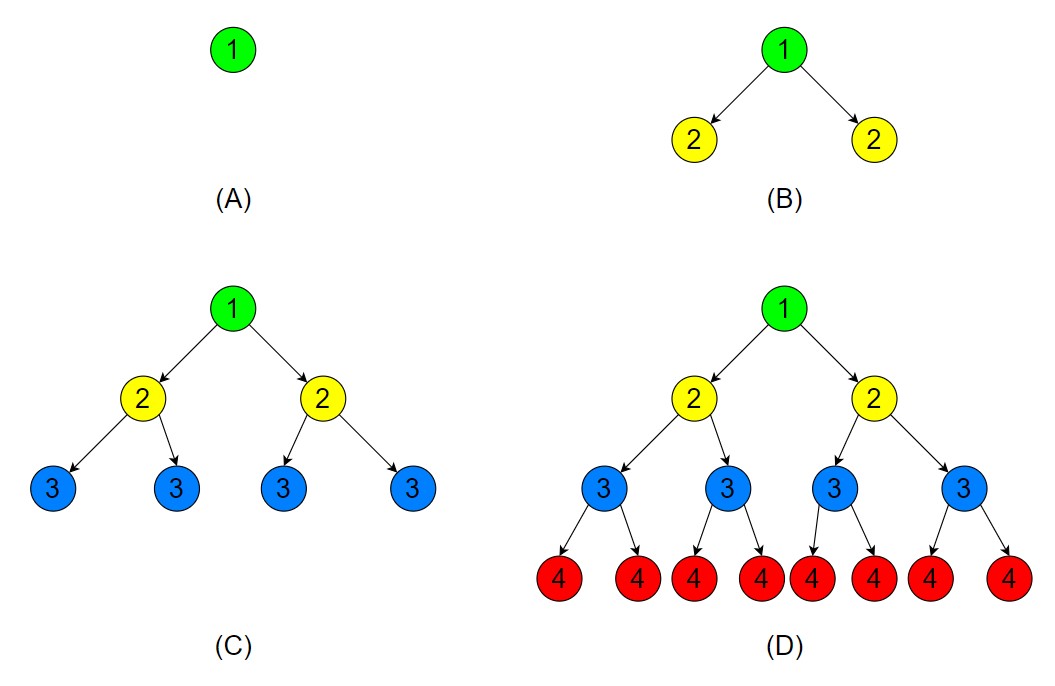
Option A is true, because in a full binary tree L = 𝐼 + 1. Generally, in a binary tree 𝐿 ≤ 𝐼 + 1.
Option B is also true, because in the figure (A) 0+1 ≤ 1 ≤ 20+1 −1 è 1 ≤ 1 ≤ 1
In figure (B) 1+1 ≤ 3 ≤ 21+1 −1 è 2 ≤ 3 ≤ 3
Check figure (C) and (D)?
Option C is also true, because in figure (A) 0 ≤ 0 ≤ 20 −1
Option D is false, because if Height is 3 and number of leaf node is 1 or 2 then H ≤ L is not always true.


