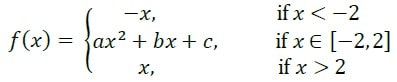SYLLABUS
Vector space, subspaces, linear dependence and independence of vectors, matrices, projection matrix, orthogonal matrix, idempotent matrix, partition matrix and their properties, quadratic forms, systems of linear equations and solutions; Gaussian elimination, eigenvalues and eigenvectors, determinant, rank, nullity, projections, LU decomposition, singular value decomposition,
Q1 – Consider the matrix
Which ONE of the following statements is TRUE?
(A) The eigenvalues of 𝑴 are non-negative and real.
(B) The eigenvalues of 𝑴 are complex conjugate pairs.
(C) One eigenvalue of 𝑴 is positive and real, and another eigenvalue of 𝑴 is zero.
(D) One eigenvalue of 𝑴 is non-negative and real, and another eigenvalue of 𝑴 is negative and real
(GATE DS&AI 2024)
Ans – (b)
Explanation – det(M−λI)=0
=> (2−λ)(1−λ)−(−1)(3)=0
=> λ² – 3λ + 5 = 0
Simplifying this equation
λ = (3 ± i√11)/2
Thus, the eigenvalues of 𝑴 are complex conjugate pairs.
Q2 – Let 𝑓:ℝ→ℝ be the function 𝑓(𝑥)=1/(1+𝑒−𝑥) . The value of the derivative of 𝑓 at 𝑥 where 𝑓(𝑥) = 0.4 is ______ (rounded off to two decimal places).
Note: ℝ denotes the set of real numbers.
(GATE DS&AI 2024)
Ans – (0.24)
Explanation – The function is f(x) = 1/(1 + e-x)
So, e-x = 1/f(x) – 1 = (1 – f(x))/f(x)
Derivative of f(x), f’(x) = -1*(1 + e-x)-2. (-e-x)
= e-x/(1+e-x)2
= (1 – f(x))*f(x)2 / f(x)
= (1 – f(x))*f(x)
= 0.6*0.4 = 0.24
Q3 – Consider the 3×3 matrix
The determinant of (𝑴𝟐+12𝑴) is ______.
(GATE DS&AI 2024)
Ans – (0)
Explanation – Determinant of (𝑴𝟐+12𝑴), so
Simplifying this M(M + 12*I) [I = identity matrix]
So, M = 1(6 – 9) – 2(18 – 12) + 3(9 – 4)
M = – 3 – 12 + 15 = 0
When determinant of M = 0, no need to calculate M + 12*I.
The answer is 0.
Q4 – Let 𝑓:ℝ→ℝ be a function. Note: ℝ denotes the set of real numbers.
Which ONE of the following choices gives the values of 𝑎, 𝑏, 𝑐 that make the function 𝑓 continuous and differentiable?
(A) 𝑎=1/4, 𝑏=0, 𝑐=1
(B) 𝑎=1/2, 𝑏=0, 𝑐=0
(C) 𝑎=0, 𝑏=0, 𝑐=0
(D) 𝑎=1, 𝑏=1, 𝑐=−4
(GATE DS&AI 2024)
Ans – (A)
Explanation – If a, b, c makes a smooth graph, if x = -2 and 2 then we can say that the graph is continuous and differentiable.
Continuous at -2 and 2
f(-2) => -(-2) = a(-2)2 + b(-2) + c
=> 4a – 2b + c = 4
f(2) => a(2)2 + b(2) + c = 2
=> 4a + 2b + c = 2
Differentiability at -2 and 2
f’(x) = -1 if x < -2
f’(x) = 2ax + b if x ϵ [-2, 2]
f’(x) = 1 if x > 2
f’(-2) => 2a(-2) + b = -1
=> 4a – b = 1
f’(2) => 2a(2) + b = 1
=> 4a + b = 1
From f’(-2) and f’(2), we get b = 0, a = ¼
From f(2), we get c = 1
Hence option A is the answer.
Q5 – Select all choices that are subspaces of ℝ3.
Note: ℝ denotes the set of real numbers.
(A) {𝐱=[𝑥1; 𝑥2; 𝑥3] ∈ ℝ3: 𝐱=𝛼[1; 1; 0] + 𝛽[1; 0; 0], 𝛼, 𝛽∈ℝ}
(B) {𝐱=[𝑥1; 𝑥2; 𝑥3] ∈ ℝ3: 𝐱=𝛼2[1; 2; 0] + 𝛽2[1; 0; 1], 𝛼, 𝛽∈ℝ}
(C) {𝐱=[𝑥1; 𝑥2; 𝑥3] ∈ ℝ3: 5𝑥1+2𝑥3 = 0, 4𝑥1−2𝑥2+3𝑥3 = 0}
(D) {𝐱=[𝑥1; 𝑥2; 𝑥3] ∈ ℝ3: 5𝑥1+2𝑥3+4 = 0}
(GATE DS&AI 2024)
Ans – (A, C)
Explanation – A subspace is a special group of vectors that follows 3 rules:
- It contains the zero vector → [0; 0; 0]
- If you add two vectors in the set, the result is also in the set
- If you multiply any vector in the set by any number, the result is still in the set
Option (A) x = α[1;1;0] + β[1;0;0], α, β ∈ R
This means the set has all vectors made by using real numbers α and β. You can choose any numbers α and β like 0, 1, –2, 3.5, etc.
Zero Vector – If α=0 and β=0,
then x = 0[1;1;0] +0[1;0;0] = [0;0;0]
So, the zero vector is in the set.
Vector Addition – x1 = α1[1;1;0] + β1[1;0;0],
x2 = α2[1;1;0] + β2[1;0;0]
Then, x1+x2=(α1+α2)[1;1;0] + (β1+β2)[1;0;0]
This is also in the set because it’s the same form.
Vector Multiplication – K is any number
Kx = Kα[1;1;0] + Kβ[1;0;0]
This is still in the set.
Hence option (A) is the answer.
Option (B) x = α2[1;2;0] + β2[1;0;1], α, β ∈ R
Here, the powers α² and β² are used.
In vector addition, α1² + α2² will be there, but we want (α1 + α2)² to fit in the set. So, option (B) is not an answer.
Option (C) 5𝑥1+2𝑥3 = 0, 4𝑥1−2𝑥2+3𝑥3 = 0
Zero Vector – Let’s say x1 = 0, x2 = 0 and x3 = 0
Both equations are correct. So, [0; 0; 0] zero vector is in the set.
Vector Addition – Let’s say [-2/5; 7/10; 1] and [0; 0; 0] are the two vectors.
In addition, 5(-2/5 + 0) + 2(1 + 0) = 0.
Also, 4(-2/5 + 0) – 2(7/10 + 0) + 3(1 + 0) = 0
Vector Multiplication – K is any number
K(5𝑥1+2𝑥3) = 0, K(4𝑥1−2𝑥2+3𝑥3) = 0
This is still in the set.
Hence, option (C) is the answer.
Option (D) 5𝑥1+2𝑥3+4 = 0
Zero Vector – Let’s say x1 = 0, x2 = 0 and x3 = 0
So, 5(0) + 2(0) + 4 ≠ 0
Hence, option (D) is not the answer.
Q6 – Which of the following statements is/are TRUE?
Note: ℝ denotes the set of real numbers.
(A) There exist 𝑴∈ℝ3×3, 𝒑∈ℝ3, and 𝒒∈ℝ3 such that 𝑴𝐱=𝒑 has a unique solution and M𝐱=𝒒 has infinite solutions.
(B) There exist 𝑴∈ℝ3×3, 𝒑∈ℝ3, and 𝒒∈ℝ3 such that 𝑴𝐱=𝒑 has no solutions and M𝐱=𝒒 has infinite solutions.
(C) There exist 𝑴∈ℝ2×3, 𝒑∈ℝ2, and 𝒒∈ℝ2 such that 𝑴𝐱=𝒑 has a unique solution and M𝐱=𝒒 has infinite solutions.
(D) There exist 𝑴∈ℝ3×2, 𝒑∈ℝ3, and 𝒒∈ℝ3 such that 𝑴𝐱=𝒑 has a unique solution and M𝐱=𝒒 has no solutions.
(GATE DS&AI 2024)
Ans – (B, D)
Explanation – Types of solutions
Unique solution – when matrix is full rank.
Infinite solutions – Happens when there are free variables.
No solution – Happens when equations contradict each other, like x + y = 2 and x + y = 5.
Matrix has 3×3 shape then it can have unique, infinite, or no solution.
Matrix has 3×2 shape it means it has more equations than variables, and the solutions is no or infinite solution, not unique.
Matrix has 2×3 shape it means it has more variables than equations, and it doesn’t have a unique solution, only infinite or no solution.
Option A is Mx = p has a unique solution. Mx = q has infinite solutions.
If Matrix has full rank, then p has a unique solution but q can not have infinite solutions. So, option A is false.
Option B is Mx = p has no solutions and Mx = q has infinite solutions.
If p has no solution, then it is not unique, also it can have infinite solutions. So, option B is True.
Option C has 2 equations and 3 variables. Mx = p has a unique solution and Mx = q has infinite solutions.
So, there are 3 variables and only 2 equations, so there is no unique solution. Option C is false.
Option D has 3 equations and 2 variables. Mx = p has a unique solution and Mx = q has infinite solutions.
So, there are 2 variables and 3 equations, so there is a unique solution and can have no solutions just because x + y = 2 and x + y = 5. They contradict each other. Option D is True.
Q7 – Let ℝ be the set of real numbers, 𝑈 be a subspace of ℝ3 and 𝑴∈ℝ3×3 be the matrix corresponding to the projection on to the subspace 𝑈.
Which of the following statements is/are TRUE?
(A) If 𝑈 is a 1-dimensional subspace of ℝ3, then the null space of 𝑴 is a 1-dimensional subspace.
(B) If 𝑈 is a 2-dimensional subspace of ℝ3, then the null space of 𝑴 is a 1-dimensional subspace.
(C) 𝑴2= 𝑴
(D) 𝑴3= 𝑴
(GATE DS&AI 2024)
Ans – (B, C, D)
Explanation – If U is a 1-dimensional subspace of ℝ3, it means the rank of M is 1. Then the null space of ℝ3 is (3 – rank) = 2-dimensional subspace. So, option A is wrong.
If U is a 2-dimensional subspace of ℝ3, it means the rank of M is 2. Then the null space of ℝ3 is (3 – rank) = 1-dimensional subspace. So, option B is True.
If M is an idempotent matrix, then M2 = M and M3 = M.
Example – M = then M2 is also
So, option C and D is also Correct.
Q8 – Let 𝒖 = [ 1; 2; 3; 4; 5] , and let 𝜎1, 𝜎2, 𝜎3, 𝜎4, 𝜎5 be the singular values of the matrix 𝑴= 𝒖𝒖𝑻 (where 𝒖𝑻 is the transpose of 𝒖). The value of Σ5i=1 𝜎i is ______.
(GATE DS&AI 2024)
Ans – (55)
Explanation – Σ5i=1 𝜎i is the sum of the singular values of matrix M.
M = 5*5 symmetric matrix and of rank 1.
M = 𝒖𝒖𝑻 = Σ5i=1 𝜎i = 12 + 22 + 32 + 42 + 52 = 55.