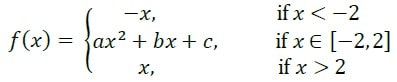Aptitude Test Q1 to Q10
Q 1 to 5 are of 1 mark
Q 6 to 10 are of 2 marks
Q1 – If ‘→’ denotes increasing order of intensity, then the meaning of the words
[sick → infirm → moribund] is analogous to [silly → _______ → daft].
Which one of the given options is appropriate to fill the blank?
(A) frown
(B) fawn
(C) vein
(D) vain
Ans – (D)
Explanation –
Sick (a little weak) → infirm (weaker) → moribund (dying) is the increasing order of intensity of people ill.
And the options are
- Frown – to show you are angry, serious, etc., by making lines appear on your forehead above your nose.
- Fawn – to show affection
- Vein – a particular style or quality or blood vessel
- Vain – proud, arrogant, pointless, selfish
silly (crazy, foolish) → _______ → daft (stupid in more intensity).
All the options are not matching, but option D can be somewhat correct. Crazy, foolish person becomes pointless.
Q2 – The 15 parts of the given figure are to be painted such that no two adjacent parts with shared boundaries (excluding corners) have the same color. The minimum number of colors required is

(A) 4
(B) 3
(C) 5
(D) 6
Ans – (A)
Explanation – This is a problem of Four-Color Algorithm. The Four-Color Problem states that any map can be coloured using no more than four colours so that no two adjacent regions share the same color.
This problem can be solved using the DSATUR algorithm, which is a specialized greedy algorithm for graph colouring.
DSATUR stands for Degree of Saturation. This algorithm is efficient and often finds a solution with the minimum number of colours. The DSATUR algorithm colours the states of a graph by selecting the state with the highest degree of saturation at each step.

The Indian map is also filled with 4 colours.
For a complete understanding, please refer to the following link – https://compgeek.co.in/four-colour-problem-by-dsatur/
Q3 – How many 4-digit positive integers divisible by 3 can be formed using only the digits {1,3,4,6,7}, such that no digit appears more than once in a number?
(A) 24
(B) 48
(C) 72
(D) 12
Ans – (B)
Explanation – In the digits 1, 3, 4, 6 and 7, we have to create 4 digits numbers, and the 4 digits sum is divisible by 3.
We have to make the four-digit numbers by {1, 4, 6, 7} or {1, 3, 4, 7}.
So, taking the digits {1, 4, 6, 7} we can create = 4*3*2*1 = 24 digits
Also, by taking the digits {1, 3, 4, 7} we can create = 4*3*2*1 = 24 digits
Sum = 48 digits
Q4 – The sum of the following infinite series is 2 + 1/2 + 1/3 + 1/4 + 1/8 + 1/9 + 1/16 + 1/27 +⋯
(A) 11/3
(B) 7/2
(C) 13/4
(D) 9/2
Ans – (B)
Explanation – Sum = 2 + 1/2 + 1/3 + 1/4 + 1/8 + 1/9 + 1/16 + 1/27 + …
These are 2 Geometric Progression that is infinite.
Sum = (1 + 1/2 + 1/4 + 1/8 + 1/16 + …) + (1 + 1/3 + 1/9 + 1/27 + …)
Sum = 1/(1 – 1/2) + 1/(1 – 1/3) = 2 + 3/2 = 7/2
Q5 – In an election, the share of valid votes received by the four candidates A, B, C, and D is represented by the pie chart shown. The total number of votes cast in the election were 1,15,000, out of which 5,000 were invalid.
Based on the data provided, the total number of valid votes received by the candidates B and C is
(A) 45,000
(B) 49,500
(C) 51,750
(D) 54,000
Ans – (B)
Explanation – Total number of votes cast = 1,15,000
Invalid votes = 5,000
Total valid votes = 1,10,000
The total number of valid votes received by the candidates B and C is = 25% of 1,10,000 + 20% of 1,10,000
Total votes = 27,500 + 22,000 = 49,500 votes
Q6 – Thousands of years ago, some people began dairy farming. This coincided with a number of mutations in a particular gene that resulted in these people developing the ability to digest dairy milk.
Based on the given passage, which of the following can be inferred?
(A) All human beings can digest dairy milk.
(B) No human being can digest dairy milk.
(C) Digestion of dairy milk is essential for human beings.
(D) In human beings, digestion of dairy milk resulted from a mutated gene.
Ans – (D)
Q7 – The probability of a boy or a girl being born is 1/2. For a family having only three children, what is the probability of having two girls and one boy?
(A) 3/8
(B) 1/8
(C) 1/4
(D) 1/2
Ans – (A)
Explanation – Girl means G and boy means B.
Three children sample space = {GGG, GGB, GBG, BGG, BBG, BGB, GBB, BBB}
Probability of having two girls and one boy = 3/8
Q8 –
Person 1 and Person 2 invest in three mutual funds A, B, and C. The amounts they invest in each of these mutual funds are given in the table.
| Mutual fund A | Mutual fund B | Mutual fund C | |
Person 1 | ₹10,000 | ₹20,000 | ₹20,000 |
|
Person 2 | ₹20,000 | ₹15,000 | ₹15,000 |
At the end of one year, the total amount that Person 1 gets is ₹500 more than Person 2. The annual rate of return for the mutual funds B and C is 15% each. What is the annual rate of return for the mutual fund A?
(A) 7.5%
(B) 10%
(C) 15%
(D) 20%
Ans – (B)
Explanation – Let the annual rate of return for the mutual fund A = x%
Rate of return for the mutual fund B = 15%
Rate of return for the mutual fund C = 15%
Total Return for Person 1 = (100*x + 200*15 + 200*15)
= 100*x + 6000
Total Return for Person 2 = (200*x + 150*15 + 150*15)
= 200*x + 4500
At the end of one year, the total amount that Person 1 gets is ₹500 more than Person 2.
So, 100*x + 6000 = 200*x + 4500 + 500
=> 100*x = 1000
=> x = 10
The annual rate of return for Mutual Fund A is 10%.
Q9 – Three different views of a dice are shown in the figure below.

The piece of paper that can be folded to make this dice is

Ans – (A)
Q10 – Visualize two identical right circular cones such that one is inverted over the other and they share a common circular base. If a cutting plane passes through the vertices of the assembled cones, what shape does the outer boundary of the resulting cross-section make?
(A) A rhombus
(B) A triangle
(C) An ellipse
(D) A hexagon
Ans – (A)
Explanation –

Outer boundary of the cross section makes a rhombus shape.
Subject Specific – Computer Science
Q11 to 35 are of 1 mark
Q11 – Consider the following statements:
(i) The mean and variance of a Poisson random variable are equal.
(ii) For a standard normal random variable, the mean is zero and the variance is one.
Which ONE of the following options is correct?
(A) Both (i) and (ii) are true
(B) (i) is true and (ii) is false
(C) (ii) is true and (i) is false
(D) Both (i) and (ii) are false
Ans – (A)
Explanation – Events that occurred in a fixed amount of time or space are counted by Poisson distribution.
For example, around 5 cars cross in a signal within an average of 1 minute.
Thus, the average number of cars is 5 and so must be variance.
In other words, the statement (i) is true.
The normal distribution also known as the “bell curve” shape, is probably one of the most well know distributions in statistics.
Standard normal means that the curve is centred at 0. (Mean = 0)
No stretching, no compression. (Variance = 1)
It means statement (ii) is also correct.
Q12 – Three fair coins are tossed independently. T is the event that two or more tosses result in heads. S is the event that two or more tosses result in tails.
What is the probability of the event 𝑇∩𝑆 ?
(A) 0
(B) 0.5
(C) 0.25
(D) 1
Ans – (A)
Explanation – 3 tosses are there and T is the event that two or more tosses result in heads and S is the event that two or more tosses result in tails. If we look at the event 𝑇∩𝑆, it means four tosses should be there. 3 tosses can’t have both 2 heads and 2 tails.
So, it means probability is 0 (either T or S will make it zero).
Q13 – Consider the matrix
 Which ONE of the following statements is TRUE?
Which ONE of the following statements is TRUE?
(A) The eigenvalues of 𝑴 are non-negative and real.
(B) The eigenvalues of 𝑴 are complex conjugate pairs.
(C) One eigenvalue of 𝑴 is positive and real, and another eigenvalue of 𝑴 is zero.
(D) One eigenvalue of 𝑴 is non-negative and real, and another eigenvalue of 𝑴 is negative and real
Ans – (B)
Explanation – det(M−λI)=0
=> (2−λ)(1−λ)−(−1)(3)=0
=> λ² – 3λ + 5 = 0
Simplifying this equation
λ = (3 ± i√11)/2
Thus, the eigenvalues of 𝑴 are complex conjugate pairs.
Q14 – Consider performing depth-first search (DFS) on an undirected and unweighted graph G starting at vertex 𝑠. For any vertex 𝑢 in G, 𝑑[𝑢] is the length of the shortest path from 𝑠 to 𝑢. Let (𝑢,𝑣) be an edge in G such that 𝑑[𝑢]<𝑑[𝑣]. If the edge (𝑢,𝑣) is explored first in the direction from 𝑢 to 𝑣 during the above DFS, then (𝑢,𝑣) becomes a ______ edge.
(A) tree
(B) cross
(C) back
(D) gray
Ans – (A)
Explanation – Now let us look at the question where we are given that d[u] < d[v], which means vertex u is nearer to the source vertex s than vertex v is. If we explore the edge (u,v) first from u to v during DFS, it means that v has not yet been visited. Hence this edge will be tree edge as it is first discovery of new vertex. Therefore, the answer is tree and it matches with option (A).
Q15 – For any twice differentiable function 𝑓:ℝ→ℝ, if at some 𝑥* ∈ ℝ, 𝑓′(𝑥*) = 0 and 𝑓′′(𝑥*) > 0, then the function 𝑓 necessarily has a ______ at 𝑥 = 𝑥*.
Note: ℝ denotes the set of real numbers.
(A) local minimum
(B) global minimum
(C) local maximum
(D) global maximum
Ans – (A)
Explanation – For a function f, if we have an f that is twice differentiable, using the first and second derivative tests can give us insight on how this function behaves. If at some point x*, the first derivative f′(x) = 0, this implies that the function has a flat slope there, and is neither increasing nor decreasing at the exact point. Now, if the second derivative f′′(x*) > 0, we have a bowl that opens towards y axis. This is evidence by the curve rising as it goes up, meaning the point x* is a Local Minimum, a point at which the function value is lower than the values of all neighbouring points. So, the answer will be option (A) a local minimum.
Q16 – Match the items in Column 1 with the items in Column 2 in the following table:
Column 1
(p) First In First Out
(q) Lookup Operation
(r) Last In First Out
Column 2
(i) Stacks
(ii) Queues
(iii) Hash Tables
(A) (p) − (ii), (q) − (iii), (r) − (i)
(B) (p) − (ii), (q) − (i), (r) − (iii)
(C) (p) − (i), (q) − (ii), (r) − (iii)
(D) (p) − (i), (q) − (iii), (r) − (ii)
Ans – (A)
Explanation – Stacks are one of the most uncomplicated types of data structures which are those that store items in a particular order — Last In, First Out (LIFO).
Queue is a linear data structure that is the simplest, least sophisticated data structure in computer science, sometimes allowing only one piece of data in it. The First In, First Out (FIFO) rule must be followed.
Hash Tables – A hash table is a data-like structure mainly composed of a key-value pair and which is quite helpful for storing the data. Its main advantage is that the hash function locates the query data immediately. The fast lookup, insertion, and deletion operations can be completed with no more than O(1) time complexity on the average, which is the main feature of the hash table.
Q17 – Consider the dataset with six datapoints: {(𝒙𝟏, 𝒚𝟏), (𝒙𝟐, 𝒚𝟐), … ,(𝒙𝟔, 𝒚𝟔)}, where
 and the labels are given by 𝒚𝟏 = 𝒚𝟐 = 𝒚𝟓 = 1, and 𝒚𝟑 = 𝒚𝟒 = 𝒚𝟔 = −1. A hard margin linear support vector machine is trained on the above dataset.
and the labels are given by 𝒚𝟏 = 𝒚𝟐 = 𝒚𝟓 = 1, and 𝒚𝟑 = 𝒚𝟒 = 𝒚𝟔 = −1. A hard margin linear support vector machine is trained on the above dataset.
Which ONE of the following sets is a possible set of support vectors?
(A) {𝒙𝟏, 𝒙𝟐, 𝒙𝟓}
(B) {𝒙𝟑, 𝒙𝟒, 𝒙𝟓}
(C) {𝒙𝟒, 𝒙𝟓}
(D) {𝒙𝟏, 𝒙𝟐, 𝒙𝟑, 𝒙𝟒}
Ans – (D)
Explanation – In a hard margin SVM, the support vectors are placed on the boundary between the margins (i.e., they are closest to the decision boundary but correctly classified). For the farther points, which are located inside their class region, the centre of the margin, they are not support vectors.
Now x1 = [1, 0], y1 = 1 is closest to the decision boundary.
Then x2 = [0, 1], y2 = 1 is closest to the decision boundary.
x3 = [0, -1], y3 = -1 is closest to the decision boundary.
x4 = [-1, 0], y4 = -1 is closest to the decision boundary.
Both x5 and x6 is far from the decision boundary, so they are not support vectors. Hence option D is the answer.
Q18 – Match the items in Column 1 with the items in Column 2 in the following table:
Column 1
(p) Principal Component Analysis
(q) Naïve Bayes Classification
(r) Logistic Regression
Column 2
(i) Discriminative Model
(ii) Dimensionality Reduction
(iii) Generative Model
(A) (p) − (iii), (q) − (i), (r) − (ii)
(B) (p) − (ii), (q) − (i), (r) − (iii)
(C) (p) − (ii), (q) − (iii), (r) − (i)
(D) (p) − (iii), (q) − (ii), (r) − (i)
Ans – (C)
Explanation – (p) Principal Component Analysis → (ii) Dimensionality Reduction
Principal Component Analysis (PCA) is a tool to lower the dimensional space of a huge data set by converting them into a smaller set of variables that still have most of the information contained in them.
(q) Naïve Bayes Classification → (iii) Generative Model
Naïve Bayes model is a kind of generative model that finds the joint probability spread of and then uses Bayes’ theorem to assess the conditional probability.
(r) Logistic Regression → (i) Discriminative Model
Logistic Regression, on the other hand, is a discriminative model that in contrast straightly estimates the conditional probability p(y∣x) without reference to the distribution of x.
Q19 – Euclidean distance based 𝑘-means clustering algorithm was run on a dataset of 100 points with 𝑘=3. If the points [1; 1] and [−1; 1] are both part of cluster 3, then which ONE of the following points is necessarily also part of cluster 3?
(A) [0; 0]
(B) [0; 2]
(C) [2; 0]
(D) [0; 1]
Ans – (D)
Explanation – The k-means algorithm is run using Euclidean distance.
k=3, and cluster 3 contains the points x1 = [1; 1], x2 = [-1; 1]
Centroid is the mean of all points in the cluster.
Centroid = ½([1; 1] + [-1; 1]) = ½([1+(-1); 1+1] = ½([0; 2] = [0; 1]
We now compute Euclidean distance from each option to the centroid [0; 1]
Option A – [0; 0]
Distance = √((0-0)2 + (0-1)2 = √1 = 1
Option B – [0; 2]
Distance = √((0-0)2 + (2-1)2 = √1 = 1
Option C – [2; 0]
Distance = √((2-0)2 + (0-1)2 = √(4 + 1) = √5
Option D – [0; 1]
Distance = √((0-0)2 + (1-1)2 = √0 = 0
So, option D is the closest and necessary part of the cluster 3.
Q20 – Given a dataset with 𝐾 binary-valued attributes (where 𝐾 > 2) for a two-class classification task, the number of parameters to be estimated for learning a naïve Bayes classifier is
(A) 2𝐾 + 1
(B) 2𝐾 + 1
(C) 2𝐾+1 + 1
(D) 𝐾2 + 1
Ans – (B)
Explanation – If there are 2 classes (such as class 0 and class 1), we will need 2 probabilities per attribute, that is, a total of 2K parameters for K binary valued attributes. Moreover, it is necessary to calculate the prior probability of one class (e.g. P(Class = 1)), as the prior probability of the other class can be recovered by subtracting this value from one. To sum up, one class prior only needs to be computed, thus the number of the parameters is increased by 1. In total, that is 2K+1 parameters that should be estimated.
Q21 – Consider performing uniform hashing on an open address hash table with load factor 𝛼 = 𝑛/𝑚 < 1, where 𝑛 elements are stored in the table with 𝑚 slots. The expected number of probes in an unsuccessful search is at most 1/(1−𝛼) .
Inserting an element in this hash table requires at most ______ probes, on average.
(A) ln(1/(1−𝛼))
(B) 1/1−𝛼
(C) 1 + 𝛼/2
(D) 1/(1+𝛼)
Ans – (B)
Explanation – We use a hash table with open addressing in data structure. With this system, we have a table with m slots (positions to keep the items), also we have n elements stored. The load factor is α = n/m, which shows how much of the table is full. Because α < 1, the table is not filled up yet.
When we want to add a new element. We go to the place where the hash function sends us first. If it is full, we go to the next position. We look for a slot where we can insert the new element, by trying one by one slot. This is a search that ends unsuccessfully because we are looking for an unoccupied slot.
In the situation of equal probability for all empty slots (i.e. uniform hashing), the expected number of probes in an unsuccessful search is 1/(1−α). As insertion is an unsuccessful search (you stop at an empty cell), the average number of probes for insertion is also 1/(1−α).
Q22 – For any binary classification dataset, let 𝑆𝐵 ∈ ℝ𝑑×𝑑 and 𝑆𝑊 ∈ ℝ𝑑×𝑑 be the between-class and within-class scatter (covariance) matrices, respectively. The Fisher linear discriminant is defined by 𝑢∗ ∈ ℝ𝑑, that maximizes
𝐽(𝑢) = 𝑢𝑇𝑆𝐵𝑢/𝑢𝑇𝑆𝑊𝑢
If 𝜆 = 𝐽(𝑢∗), 𝑆𝑊 is non-singular and 𝑆𝐵 ≠ 0, then (𝑢∗, 𝜆) must satisfy which ONE of the following equations?
Note: ℝ denotes the set of real numbers.
(A) 𝑆𝑊−1 𝑆𝐵𝑢∗ =𝜆𝑢∗
(B) 𝑆𝑊𝑢∗ = 𝜆𝑆𝐵𝑢∗
(C) 𝑆𝐵𝑆𝑊𝑢∗ = 𝜆𝑢∗
(D) 𝑢∗𝑇𝑢∗ = 𝜆2
Ans – (A)
Explanation – This question is specifically from a method called Fisher Linear Discriminant Analysis (LDA). It is used to separate two classes (binary classification).
You are given two important matrices
- SB – Between-class scatter – tells how far the two classes are from each other.
- SW – Within-class scatter – tells how spread out the data points are within each class.
Both matrices are size d × d, where d is the number of features.
We want to find a direction u (a vector) such that
- The distance between classes is large (good separation),
- The spread inside each class is small (less confusion).
This is done using a formula called Fisher’s criterion 𝐽(𝑢) = 𝑢𝑇𝑆𝐵𝑢/𝑢𝑇𝑆𝑊𝑢. It is a ratio of the class separation by noise or spread inside class. We want to find the best vector u* that gives the maximum value of J(u). This vector is the best direction to separate the two classes.
The answer is option (A) 𝑆𝑊−1 𝑆𝐵𝑢∗ =𝜆𝑢∗. This is a standard result in linear algebra. It means u* is an eigenvector of the matrix 𝑆𝑊−1 𝑆𝐵, and λ is its eigenvalue.
Q23 – Let ℎ1 and ℎ2 be two admissible heuristics used in 𝐴∗ search.
Which ONE of the following expressions is always an admissible heuristic?
(A) ℎ1 + ℎ2
(B) ℎ1 × ℎ2
(C) ℎ1/ℎ2, (ℎ2 ≠ 0)
(D) |ℎ1 − ℎ2|
Ans – (D)
Explanation – The heuristic function h(n) refers to a logical estimation of the cost of the shortest path to the goal from the given node, which is the true cost. The function h(n) is less than or equal to double h*(n) function.
There are two admissible heuristics, namely, h1 and h2. So, the next task is to always check which of the combinations is admissible.
Option (A) – h1 + h2
The heuristic is not always admissible. If the sum of the two heuristics is less than or equal to the true cost, then it will always be admissible, the example of that is both are equal to the exact cost. So may overestimate.
Option (B) – h1 × h2
If either one is too big, then the result will be too big too. Again, can overestimate that’s why it is not always admissible.
Option (C) – h1/h2 (when ℎ2 ≠ 0)
If division the two heuristics will not guarantee the result to be less than or equal to the true cost.
Example – h*(n) = 10, h1 = 5 and h2 = 0.2 then h1/h2 = 25. That is why it is not always admissible.
Option (D) – ∣h1 − h2∣
The absolute difference between two admissible heuristics. Since the result is always positive and the heuristics are both less than the true cost, the difference between them is also always less than the true cost. Therefore this will not mislead the cost and it is always admissible.
So, option (D) is the answer.
Q24 – Consider five random variables 𝑈, 𝑉, 𝑊, 𝑋, and 𝑌 whose joint distribution satisfies:
𝑃(𝑈,𝑉,𝑊,𝑋,𝑌) = 𝑃(𝑈)𝑃(𝑉)𝑃(𝑊|𝑈,𝑉)𝑃(𝑋|𝑊)𝑃(𝑌|𝑊)
Which ONE of the following statements is FALSE?
(A) 𝑌 is conditionally independent of 𝑉 given 𝑊
(B) 𝑋 is conditionally independent of 𝑈 given 𝑊
(C) 𝑈 and 𝑉 are conditionally independent given 𝑊
(D) 𝑌 and 𝑋 are conditionally independent given 𝑊
Ans – (C)
Explanation – This is a Bayesian Network Design or a Probabilistic Graphical Model Design in which
- U is independent
- V is independent
- W is dependent on both U and V.
- X is dependent on W
- Y is also dependent on W

Option A – True because Y and V having no edge.
Option B – True because X and U having no edge.
Option C – False because U and V are dependent on W.
Option D – True because W having and edge and is dependent on X and Y not vice versa.
Q25 – Consider the following statement:
In adversarial search, 𝛼–𝛽 pruning can be applied to game trees of any depth where 𝛼 is the (m) value choice we have formed so far at any choice point along the path for the MAX player and 𝛽 is the (n) value choice we have formed so far at any choice point along the path for the MIN player.
Which ONE of the following choices of (m) and (n) makes the above statement valid?
(A) (m) = highest, (n) = highest
(B) (m) = lowest, (n) = highest
(C) (m) = highest, (n) = lowest
(D) (m) = lowest, (n) = lowest
Ans – (C)
Explanation – α–β pruning helps to minimize the number of nodes that need to be visited in a minimax game tree.
- α (alpha) means (m) is the highest value found along the path for MAX (the player who tries to get the maximum value).
- β (beta) means (n) is the lowest value found along the path for MIN (the player who tries to get the minimum value).
Q26 – Consider a database that includes the following relations:
Defender(name, rating, side, goals)
Forward(name, rating, assists, goals)
Team(name, club, price)
Which ONE of the following relational algebra expressions checks that every name occurring in Team appears in either Defender or Forward, where 𝜙 denotes the empty set?
(A) Π𝑛𝑎𝑚𝑒(Team)∖(Π𝑛𝑎𝑚𝑒(Defender)∩Π𝑛𝑎𝑚𝑒(Forward)) = 𝜙
(B) (Π𝑛𝑎𝑚𝑒(Defender)∩Π𝑛𝑎𝑚𝑒(Forward))∖Π𝑛𝑎𝑚𝑒(Team) = 𝜙
(C) Π𝑛𝑎𝑚𝑒(Team)∖(Π𝑛𝑎𝑚𝑒(Defender)∪Π𝑛𝑎𝑚𝑒(Forward)) = 𝜙
(D) (Π𝑛𝑎𝑚𝑒(Defender)∪Π𝑛𝑎𝑚𝑒(Forward))∖Π𝑛𝑎𝑚𝑒(Team) = 𝜙
Ans – (C)
Explanation – Every name occurring in Team appears in either Defender or Forward, it means Π𝑛𝑎𝑚𝑒(Team)∖(Π𝑛𝑎𝑚𝑒(Defender) ∪ Π𝑛𝑎𝑚𝑒(Forward)) = 𝜙
Q27 – Let the minimum, maximum, mean and standard deviation values for the attribute income of data scientists be ₹46000, ₹170000, ₹96000, and ₹21000, respectively. The z-score normalized income value of ₹106000 is closest to which ONE of the following options?
(A) 0.217
(B) 0.476
(C) 0.623
(D) 2.304
Ans – (B)
Explanation – The z-score normalized income value = (106000 – mean)/standard deviation
= (106000 – 96000)/21000
= 0.476 is the answer (option B).
Q28 – Consider the following tree traversals on a full binary tree:
(i) Preorder
(ii) Inorder
(iii) Postorder
Which of the following traversal options is/are sufficient to uniquely reconstruct the full binary tree?
(A) (i) and (ii)
(B) (ii) and (iii)
(C) (i) and (iii)
(D) (ii) only
Ans – (A, B, C)
Explanation – We have three tree traversals technique on a binary tree. Basically, if we are given an inorder traversal of binary tree and a preorder or postorder traversal of a binary tree, then we can uniquely draw the diagram of such binary tree. Only two are necessary to create a diagram uniquely (Inorder – Preorder) or (Inorder – Postorder).
But in the question, we make a full binary tree, then preorder traversal and postorder traversal alone are sufficient to create the tree uniquely.
Q29 – Let 𝑥 and 𝑦 be two propositions. Which of the following statements is a tautology /are tautologies?
(A) (¬𝑥∧𝑦 )⟹(𝑦⟹𝑥)
(B) (𝑥∧¬𝑦 )⟹(¬𝑥⟹𝑦)
(C) (¬𝑥∧𝑦 )⟹(¬𝑥⟹𝑦)
(D) (𝑥∧¬𝑦 )⟹(𝑦⟹𝑥)
Ans – (B, C, D)
Explanation –
Option A – Not a tautology
x | y | ¬𝑥 | ¬𝑦 | ¬𝑥∧𝑦 | 𝑦⟹𝑥 | (¬𝑥∧𝑦) ⟹(𝑦⟹𝑥) |
F | F | T | T | F | T | T |
F | T | T | F | T | F | F |
T | F | F | T | F | T | T |
T | T | F | F | F | T | T |
Option B – Tautology
x | y | ¬𝑥 | ¬𝑦 | 𝑥∧¬𝑦 | ¬𝑥⟹y | (𝑥∧¬𝑦) ⟹(¬𝑥⟹𝑦) |
F | F | T | T | F | F | T |
F | T | T | F | F | T | T |
T | F | F | T | T | T | T |
T | T | F | F | F | T | T |
Option C – Tautology
x | y | ¬𝑥 | ¬𝑦 | ¬𝑥∧𝑦 | ¬𝑥⟹y | (¬𝑥∧𝑦 )⟹(¬𝑥⟹𝑦) |
F | F | T | T | F | F | T |
F | T | T | F | T | T | T |
T | F | F | T | F | T | T |
T | T | F | F | F | T | T |
Option D – Tautology
x | y | ¬𝑥 | ¬𝑦 | 𝑥∧¬𝑦 | y ⟹ x | (𝑥∧¬𝑦 )⟹(𝑦⟹𝑥) |
F | F | T | T | F | T | T |
F | T | T | F | F | F | T |
T | F | F | T | T | T | T |
T | T | F | F | F | T | T |
Q30 – Consider sorting the following array of integers in ascending order using an in-place Quicksort algorithm that uses the last element as the pivot.
60 | 70 | 80 | 90 | 100 |
The minimum number of swaps performed during this Quicksort is ______.
Ans – (0)
Explanation –
The array is already sorted but we have to perform quick sort algorithm that the swap happens or not.
Quick Sort
Partitioning Using Nico Lomuto Scheme Algorithm
function partition(array, low, high)
pi = array[high] // Choose last element as pivot (pi)
i = low – 1 // Maintain index i to separate elements from larger ones.
for j = low to high – 1 // Traverse the array
if array[j] <= pivot
i = i + 1
swap array[i] with array[j]
// Swap smaller elements before the pivot
swap array[i + 1] with array[high]
return i + 1
There would be no number swapped in the original array, so number of swaps would be 0.
Q31 – Consider the following two tables named Raider and Team in a relational database maintained by a Kabaddi league. The attribute ID in table Team references the primary key of the Raider table, ID.
Raider | |||
ID | Name | Raids | Raid Points |
1 | Arjun | 200 | 250 |
2 | Ankush | 190 | 219 |
3 | Sunil | 150 | 200 |
4 | Reza | 150 | 190 |
5 | Pratham | 175 | 220 |
6 | Gopal | 193 | 215 |
Team | ||
City | ID | Bid Points |
Jaipur | 2 | 200 |
Patna | 3 | 195 |
Hyderabad | 5 | 175 |
Jaipur | 1 | 250 |
Patna | 4 | 200 |
Jaipur | 6 | 200 |
The SQL query described below is executed on this database:
SELECT *
FROM Raider, Team
WHERE Raider.ID=Team.ID AND City=“Jaipur” AND RaidPoints > 200;
The number of rows returned by this query is ______.
Ans – (3)
Explanation – The number of rows returned by this query is
ID | Name | Raid | Raid Point | City | Bid Point |
1 | Arjun | 200 | 250 | Jaipur | 250 |
2 | Ankush | 190 | 219 | Jaipur | 200 |
6 | Gopal | 193 | 215 | Jaipur | 200 |
Q32 – The fundamental operations in a double-ended queue D are:
insertFirst(e) – Insert a new element e at the beginning of D.
insertLast(e) – Insert a new element e at the end of D.
removeFirst() – Remove and return the first element of D.
removeLast() – Remove and return the last element of D.
In an empty double-ended queue, the following operations are performed:
insertFirst(10)
insertLast(32)
a ←removeFirst()
insertLast(28)
insertLast(17)
a ←removeFirst()
a ← removeLast()
The value of a is ______.
Ans – (17)
Explanation – The double ended queue D = [ ]
Step 1 – insertFirst(10), D = [10]
Step 2 – insertLast(32), D = [10, 32]
Step 3 – a ←removeFirst(), D = [32], a = 10
Step 4 – insertlast(28), D = [32, 28]
Step 5 – insertlast(17), D = [32, 28, 17]
Step 6 – a ←removeFirst(), D = [28, 17], a = 32
Step 7 – a ← removeLast(), D = [28], a = 17
The value of a is 17.
Q33 – Let 𝑓:ℝ→ℝ be the function 𝑓(𝑥)=1/(1+𝑒−𝑥) . The value of the derivative of 𝑓 at 𝑥 where 𝑓(𝑥) = 0.4 is ______ (rounded off to two decimal places).
Note: ℝ denotes the set of real numbers.
Ans – (0.24)
Explanation – The function is f(x) = 1/(1 + e-x)
So, e-x = 1/f(x) – 1 = (1 – f(x))/f(x)
Derivative of f(x), f’(x) = -1*(1 + e-x)-2. (-e-x)
= e-x/(1+e-x)2
= (1 – f(x))*f(x)2 / f(x)
= (1 – f(x))*f(x)
= 0.6*0.4 = 0.24
Q34 – The sample average of 50 data points is 40. The updated sample average after including a new data point taking the value of 142 is ______.
Ans – (42)
Explanation – Sample average of 50 data points = 40
Let’s say there are 50 data points each of 40 values.
51th data points is 142.
Average = (50*40 + 142)/51 = 42
Q35 – Consider the 3×3 matrix
The determinant of (𝑴𝟐+12𝑴) is ______.
Ans – (0)
Explanation – Determinant of (𝑴𝟐+12𝑴), so
Simplifying this M(M + 12*I) [I = identity matrix]
So, M = 1(6 – 9) – 2(18 – 12) + 3(9 – 4)
M = – 3 – 12 + 15 = 0
When determinant of M = 0, no need to calculate M + 12*I.
The answer is 0.
Q36 – 65 are of 2 marks
Q36 – A fair six-sided die (with faces numbered 1, 2, 3, 4, 5, 6) is repeatedly thrown independently.
What is the expected number of times the die is thrown until two consecutive throws of even numbers are seen?
(A) 2
(B) 4
(C) 6
(D) 8
Ans – (C)
Explanation –
Q37 – Let 𝑓:ℝ→ℝ be a function. Note: ℝ denotes the set of real numbers.

Which ONE of the following choices gives the values of 𝑎, 𝑏, 𝑐 that make the function 𝑓 continuous and differentiable?
(A) 𝑎=1/4, 𝑏=0, 𝑐=1
(B) 𝑎=1/2, 𝑏=0, 𝑐=0
(C) 𝑎=0, 𝑏=0, 𝑐=0
(D) 𝑎=1, 𝑏=1, 𝑐=−4
Ans – (A)
Explanation – If a, b, c makes a smooth graph, if x = -2 and 2 then we can say that the graph is continuous and differentiable.
Continuous at -2 and 2
f(-2) => -(-2) = a(-2)2 + b(-2) + c
=> 4a – 2b + c = 4
f(2) => a(2)2 + b(2) + c = 2
=> 4a + 2b + c = 2
Differentiability at -2 and 2
f’(x) = -1 if x < -2
f’(x) = 2ax + b if x ϵ [-2, 2]
f’(x) = 1 if x > 2
f’(-2) => 2a(-2) + b = -1
=> 4a – b = 1
f’(2) => 2a(2) + b = 1
=> 4a + b = 1
From f’(-2) and f’(2), we get b = 0, a = ¼
From f(2), we get c = 1
Hence option A is the answer.
Q38 – Consider the following Python code:
def count(child_dict, i):
if i not in child_dict.keys():
return 1
ans = 1
for j in child_dict[i]:
ans += count(child_dict, j)
return ans
child_dict = dict()
child_dict[0] = [1, 2]
child_dict[1] = [3, 4, 5]
child_dict[2] = [6, 7, 8]
print(count(child_dict,0))
Which ONE of the following is the output of this code?
(A) 6
(B) 1
(C) 8
(D) 9
Ans – (D)
Explanation – The code counts the total number of nodes from node 0 through the use of a dictionary called child_dict to indicate the tree structure.
Start with 0 → count = 1
Go to 1
count = 1 for [1] + 1 for [3] + 1 for [4] + 1 for [5] = 4
Go to 2
count = 1 for [2] + 1 for [6] + 1 for [7] + 1 for [8] = 4
Now total count = 1 (for 0) + 4 (from 1 left subtree) + 4 (from 2 right subtree) = 9
Q39 – Consider the function computeS(X) whose pseudocode is given below:
computeS(X)
𝑆[1]←1
for 𝑖 ←2 to 𝑙𝑒𝑛𝑔𝑡ℎ(𝑋)
𝑆[𝑖]←1
if 𝑋[𝑖−1]≤𝑋[𝑖]
𝑆[𝑖]←𝑆[𝑖]+𝑆[𝑖−1]
end if
end for
return S
Which ONE of the following values is returned by the function computeS(X) for X = [6, 3, 5, 4, 10]?
(A) [1, 1, 2, 3, 4]
(B) [1, 1, 2, 3, 3]
(C) [1, 1, 2, 1, 2]
(D) [1, 1, 2, 1, 5]
Ans – (C)
Explanation – X = [6, 3, 5, 4, 10]
Dry run –
S[1] ← 1
So, S = [1, _, _, _, _]
for 𝑖 ←2 to 𝑙𝑒𝑛𝑔𝑡ℎ(𝑋)
i = 2
- X[1] = 6, X[2] = 3
- 6 ≤ 3 is false, so
- S[2] = 1
- S = [1, 1, _, _, _]
i = 3
- X[2] = 3, X[3] = 5
- 3 ≤ 5 is true, so
- S[3] = 1 + S[2] = 1 + 1 = 2
- S = [1, 1, 2, _, _]
i = 4
- X[3] = 5, X[4] = 4
- 5 ≤ 4 is false, so
- S[4] = 1
- S = [1, 1, 2, 1, _]
i = 5
- X[4] = 4, X[5] = 10
- 4 ≤ 10 is true, so
- S[5] = 1 + S[4] = 1 + 1 = 2
- S = [1, 1, 2, 1, 2]
Hence option C is the answer.
Q40 – Let 𝐹(𝑛) denote the maximum number of comparisons made while searching for an entry in a sorted array of size 𝑛 using binary search.
Which ONE of the following options is TRUE?
(A) 𝐹(𝑛)=𝐹(⌊𝑛/2⌋)+1
(B) 𝐹(𝑛)=𝐹(⌊𝑛/2⌋)+𝐹(⌈𝑛/2⌉)
(C) 𝐹(𝑛)=𝐹(⌊𝑛/2⌋)
(D) 𝐹(𝑛)=𝐹(𝑛−1)+1
Ans – (A)
Explanation – For an array of size n, the largest number of comparisons that can be done (in the worst-case scenario).
1. It picks the middle with 1 comparison.
2. Then it looks for one half, of size ⌊n/2⌋ (or smaller).
So, option A is the answer.
Q41 – Consider the following Python function:
def fun(D, s1, s2):
if s1 < s2:
D[s1], D[s2] = D[s2], D[s1]
fun(D, s1+1, s2-1)
What does this Python function fun() do? Select the ONE appropriate option below.
(A) It finds the smallest element in D from index s1 to s2, both inclusive.
(B) It performs a merge sort in-place on this list D between indices s1 and s2, both inclusive.
(C) It reverses the list D between indices s1 and s2, both inclusive.
(D) It swaps the elements in D at indices s1 and s2, and leaves the remaining elements unchanged.
Ans – (C)
Explanation – The function checks if s1 < s2. If true,
- It swaps elements at positions s1 and s2.
- Then it calls itself recursively with s1+1 and s2-1.
This continues until s1 >= s2, which is the stopping condition.
This is a classic in-place reversal of the list segment from s1 to s2. It swaps the first and last, then the second and second-last, and so on.
Let’s say D = [37, 49, 78, 61]
fun(D, 0, 3)
- Swap D[0] and D[3] → swap 37 and 61
- List becomes: [61, 49, 78, 37]
- Recursive call: fun(D, 1, 2)
fun(D, 1, 2)
- Swap D[1] and D[2] → swap 49 and 78
- List becomes: [61, 78, 49, 37]
- Recursive call: fun(D, 2, 1)
fun(D, 2, 1)
- s1 < s2 is false → recursion stops.
The list has been reversed [61, 78, 49, 37] from index 0 to 3 (inclusive).
Q42 – Consider the table below, where the (𝑖,𝑗)𝑡ℎ element of the table is the distance between points 𝑥𝑖 and 𝑥𝑗. Single linkage clustering is performed on data points, 𝑥1, 𝑥2, 𝑥3, 𝑥4, 𝑥5.
| 𝑥1 | 𝑥2 | 𝑥3 | 𝑥4 | 𝑥5 |
𝑥1 | 0 | 1 | 4 | 3 | 6 |
𝑥2 | 1 | 0 | 3 | 5 | 3 |
𝑥3 | 4 | 3 | 0 | 2 | 5 |
𝑥4 | 3 | 5 | 2 | 0 | 1 |
𝑥5 | 6 | 3 | 5 | 1 | 0 |
Which ONE of the following is the correct representation of the clusters produced?

Ans – (A)
Explanation – In this table, what is the minimum distance from one node to another node, it is 1.
(x1 distance to x2 and vice versa) = 1
Also, (x4 distance to x5 and vice versa) = 1
So, they are closely forming a new cluster.
First cluster is – (x1, x2)
Second cluster is – (x4, x5)
Option C and D are ruled out because they are not forming a cluster between x4 and x5.
Min. Distance | (x1, x2) | (x3) | (x4, x5) |
(x1, x2) | 0 | 3 | 3 |
(x3) | 3 | 0 | 2 |
(x4, x5) | 3 | 2 | 0 |
The minimum distance is 2.
(x3 distance to x4 and vice versa) = 2
So, x3 will build a new cluster with x4, and x4 and x5 already made a cluster, so its representation is (x3, (x4, x5)).
Option B is also ruled out because they are forming a cluster between ((x1, x2), x3).
Min. Distance | (x1, x2) | (x3, (x4, x5)) |
(x1, x2) | 0 | 3 |
(x3, (x4, x5)) | 3 | 0 |
The minimum distance is 3.
((x1, x2) distance to (x3, (x4, x5)) and vice versa) = 3
So, (x1, x2) will build a new cluster with (x3, (x4, x5)) and its representation is ((x1, x2), (x3, (x4, x5))).
Hence option A is the answer.
Q43 – Consider the two neural networks (NNs) shown in Figures 1 and 2, with 𝑅𝑒𝐿𝑈 activation (𝑅𝑒𝐿𝑈(𝑧) = max{0, 𝑧}, ∀𝑧 ∈ ℝ). ℝ denotes the set of real numbers. The connections and their corresponding weights are shown in the Figures. The biases at every neuron are set to 0. For what values of 𝑝, 𝑞, 𝑟 in Figure 2 are the two NNs equivalent, when 𝑥1, 𝑥2, 𝑥3 are positive?
Figure 1
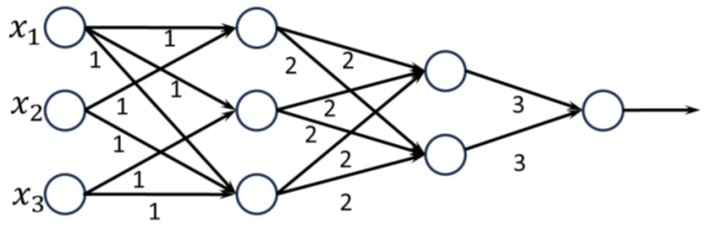
Figure 2

(A) 𝑝=36, 𝑞=24, 𝑟=24
(B) 𝑝=24, 𝑞=24, 𝑟=36
(C) 𝑝=18, 𝑞=36, 𝑟=24
(D) 𝑝=36, 𝑞=36, 𝑟=36
Ans – (A)
Explanation – While one is a big and complex neural network (Figure 1), the other one is small and simple (Figure 2). Both of them require three inputs x1, x2, x3.
Also, they will both give the same final output.
They both are applying ReLU activation. As for ReLU, the abbreviation from Rectified Linear Unit is used. While the input is a positive value, ReLU is a function that follows the straight y=x line, so the return value will be the same. If the input is a zero value or a negative one, then ReLU gives zero back.
Furthermore, the bias of all the neurons is 0. bias is just a number to which the sum of the inputs is being added. That is, there are no biases.
Furthermore, there are 6 paths leading from x1 to the output.
Each path provides the following set of weights “1 (from x to 1st layer) + 2 (from 1st layer to 2nd layer) + 3 (from 2nd layer to final output) = 6 weight.
So the overall contribution from x1 (means p in figure 2) to the output is 6×6 = 36.
At the same time, there are 4 ways leading from x2 to the output.
Each path provides 6 weight.
So the overall contribution from x2 (means q in figure 2) to the output is 4×6 = 24.
At the same time, there are 4 ways leading from x3 to the output.
Each path provides 6 weight.
So the overall contribution from x3 (means r in figure 2) to the output is 4×6 = 24.
Q44 – Consider a state space where the start state is number 1. The successor function for the state numbered n returns two states numbered n+1 and n+2. Assume that the states in the unexpanded state list are expanded in the ascending order of numbers and the previously expanded states are not added to the unexpanded state list.
Which ONE of the following statements about breadth-first search (BFS) and depth-first search (DFS) is true, when reaching the goal state number 6?
(A) BFS expands more states than DFS.
(B) DFS expands more states than BFS.
(C) Both BFS and DFS expand equal number of states.
(D) Both BFS and DFS do not reach the goal state number 6.
Ans – (C)
Explanation – We have to start with state number 1.
The successor function for the state numbered n returns two states numbered n+1 and n+2.
Means if the successor function for 1, returns 2 and 3.
The states in the unexpanded state list are expanded in the ascending order of numbers that is 1, 2, 3, 4,…
The previously expanded states are not added to the unexpanded state list.
In BFS, it is expanded, level by level, but in DFS, goes deep inside the path and then backtrack if needed.

Hence, the option (C) is the correct answer.
Q45 – Consider the following sorting algorithms:
(i) Bubble sort
(ii) Insertion sort
(iii) Selection sort
Which ONE among the following choices of sorting algorithms sorts the numbers in the array [4, 3, 2, 1, 5] in increasing order after exactly two passes over the array?
(A) (i) only
(B) (iii) only
(C) (i) and (iii) only
(D) (ii) and (iii) only
Ans – (B)
Explanation –
Bubble Sort
Input – [4, 3, 2, 1, 5]
Pass 1st – [3, 2, 1, 4, 5]
Pass 2nd – [2, 1, 3, 4, 5]
Not sorted in increasing order.
You can check here – https://compgeek.co.in/bubble-sort/
Insertion Sort
Input – [4, 3, 2, 1, 5]
Pass 1st – [4 sorted | unsorted 3, 2, 1, 5]
Pass 2nd – [3, 4 sorted | unsorted 2, 1, 5]
Not sorted in increasing order.
You can check here – https://compgeek.co.in/insertion-sort/
Selection Sort
Input – [4, 3, 2, 1, 5]
Pass 1st – [1, 3, 2, 4, 5]
Pass 2nd – [1, 2, 3, 4, 5]
It is sorted in increasing order.
You can check here – https://compgeek.co.in/selection-sort/
Q46 – Given the relational schema 𝑅=(𝑈,𝑉,𝑊,𝑋,𝑌,𝑍) and the set of functional dependencies:
{𝑈→𝑉, 𝑈→𝑊, 𝑊𝑋→𝑌, 𝑊𝑋→𝑍, 𝑉→𝑋}
Which of the following functional dependencies can be derived from the above set?
(A) 𝑉𝑊→𝑌𝑍
(B) 𝑊𝑋→𝑌𝑍
(C) 𝑉𝑊→𝑈
(D) 𝑉𝑊→𝑌
Ans – (A, B, D)
Explanation –
Option A – 𝑉𝑊→𝑌𝑍
Functional dependencies are 𝑉→𝑋 and 𝑊𝑋→𝑌, 𝑊𝑋→𝑍.
In 𝑊𝑋→𝑌, you can replace X from V, because X is dependent on V. So, 𝑊V→𝑌
Also, in 𝑊𝑋→𝑍, you can replace X from V, So, it becomes 𝑊V→𝑍.
Since 𝑊V→𝑌 and 𝑊V→𝑍, option (A) 𝑉𝑊→𝑌𝑍 is correct.
Option B – 𝑊𝑋→𝑌𝑍
Since 𝑊𝑋→𝑌 and 𝑊𝑋→𝑍, it becomes 𝑊𝑋→𝑌Z. So, option (B) is correct.
Option C – 𝑉𝑊→𝑈
In functional dependencies, there isn’t a dependency in which U comes on the right-hand side. So, option (C) is incorrect.
Option D – 𝑉𝑊→𝑌
In proving option (A), we have proved 𝑊V→𝑌, So, option (D) is correct.
Q47 – Select all choices that are subspaces of ℝ3.
Note: ℝ denotes the set of real numbers.
(A) {𝐱=[𝑥1; 𝑥2; 𝑥3] ∈ ℝ3: 𝐱=𝛼[1; 1; 0] + 𝛽[1; 0; 0], 𝛼, 𝛽∈ℝ}
(B) {𝐱=[𝑥1; 𝑥2; 𝑥3] ∈ ℝ3: 𝐱=𝛼2[1; 2; 0] + 𝛽2[1; 0; 1], 𝛼, 𝛽∈ℝ}
(C) {𝐱=[𝑥1; 𝑥2; 𝑥3] ∈ ℝ3: 5𝑥1+2𝑥3 = 0, 4𝑥1−2𝑥2+3𝑥3 = 0}
(D) {𝐱=[𝑥1; 𝑥2; 𝑥3] ∈ ℝ3: 5𝑥1+2𝑥3+4 = 0}
Ans – (A, C)
Explanation –
A subspace is a special group of vectors that follows 3 rules:
- It contains the zero vector → [0; 0; 0]
- If you add two vectors in the set, the result is also in the set
- If you multiply any vector in the set by any number, the result is still in the set
Option (A) x = α[1;1;0] + β[1;0;0], α, β ∈ R
This means the set has all vectors made by using real numbers α and β. You can choose any numbers α and β like 0, 1, –2, 3.5, etc.
Zero Vector – If α=0 and β=0,
then x = 0[1;1;0] +0[1;0;0] = [0;0;0]
So, the zero vector is in the set.
Vector Addition – x1 = α1[1;1;0] + β1[1;0;0],
x2 = α2[1;1;0] + β2[1;0;0]
Then, x1+x2=(α1+α2)[1;1;0] + (β1+β2)[1;0;0]
This is also in the set because it’s the same form.
Vector Multiplication – K is any number
Kx = Kα[1;1;0] + Kβ[1;0;0]
This is still in the set.
Hence option (A) is the answer.
Option (B) x = α2[1;2;0] + β2[1;0;1], α, β ∈ R
Here, the powers α² and β² are used.
In vector addition, α1² + α2² will be there, but we want (α1 + α2)² to fit in the set. So, option (B) is not an answer.
Option (C) 5𝑥1+2𝑥3 = 0, 4𝑥1−2𝑥2+3𝑥3 = 0
Zero Vector – Let’s say x1 = 0, x2 = 0 and x3 = 0
Both equations are correct. So, [0; 0; 0] zero vector is in the set.
Vector Addition – Let’s say [-2/5; 7/10; 1] and [0; 0; 0] are the two vectors.
In addition, 5(-2/5 + 0) + 2(1 + 0) = 0.
Also, 4(-2/5 + 0) – 2(7/10 + 0) + 3(1 + 0) = 0
Vector Multiplication – K is any number
K(5𝑥1+2𝑥3) = 0, K(4𝑥1−2𝑥2+3𝑥3) = 0
This is still in the set.
Hence, option (C) is the answer.
Option (D) 5𝑥1+2𝑥3+4 = 0
Zero Vector – Let’s say x1 = 0, x2 = 0 and x3 = 0
So, 5(0) + 2(0) + 4 ≠ 0
Hence, option (D) is not the answer.
Q48 – Which of the following statements is/are TRUE?
Note: ℝ denotes the set of real numbers.
(A) There exist 𝑴∈ℝ3×3, 𝒑∈ℝ3, and 𝒒∈ℝ3 such that 𝑴𝐱=𝒑 has a unique solution and M𝐱=𝒒 has infinite solutions.
(B) There exist 𝑴∈ℝ3×3, 𝒑∈ℝ3, and 𝒒∈ℝ3 such that 𝑴𝐱=𝒑 has no solutions and M𝐱=𝒒 has infinite solutions.
(C) There exist 𝑴∈ℝ2×3, 𝒑∈ℝ2, and 𝒒∈ℝ2 such that 𝑴𝐱=𝒑 has a unique solution and M𝐱=𝒒 has infinite solutions.
(D) There exist 𝑴∈ℝ3×2, 𝒑∈ℝ3, and 𝒒∈ℝ3 such that 𝑴𝐱=𝒑 has a unique solution and M𝐱=𝒒 has no solutions.
Ans – (B, D)
Explanation – Types of solutions
Unique solution – when matrix is full rank.
Infinite solutions – Happens when there are free variables.
No solution – Happens when equations contradict each other, like x + y = 2 and x + y = 5.
Matrix has 3×3 shape then it can have unique, infinite, or no solution.
Matrix has 3×2 shape it means it has more equations than variables, and the solutions is no or infinite solution, not unique.
Matrix has 2×3 shape it means it has more variables than equations, and it doesn’t have a unique solution, only infinite or no solution.
Option A is Mx = p has a unique solution. Mx = q has infinite solutions.
If Matrix has full rank, then p has a unique solution but q can not have infinite solutions. So, option A is false.
Option B is Mx = p has no solutions and Mx = q has infinite solutions.
If p has no solution, then it is not unique, also it can have infinite solutions. So, option B is True.
Option C has 2 equations and 3 variables. Mx = p has a unique solution and Mx = q has infinite solutions.
So, there are 3 variables and only 2 equations, so there is no unique solution. Option C is false.
Option D has 3 equations and 2 variables. Mx = p has a unique solution and Mx = q has infinite solutions.
So, there are 2 variables and 3 equations, so there is a unique solution and can have no solutions just because x + y = 2 and x + y = 5. They contradict each other. Option D is True.
Q49 – Let ℝ be the set of real numbers, 𝑈 be a subspace of ℝ3 and 𝑴∈ℝ3×3 be the matrix corresponding to the projection on to the subspace 𝑈.
Which of the following statements is/are TRUE?
(A) If 𝑈 is a 1-dimensional subspace of ℝ3, then the null space of 𝑴 is a 1-dimensional subspace.
(B) If 𝑈 is a 2-dimensional subspace of ℝ3, then the null space of 𝑴 is a 1-dimensional subspace.
(C) 𝑴2= 𝑴
(D) 𝑴3= 𝑴
Ans – (B, C, D)
Explanation – If U is a 1-dimensional subspace of ℝ3, it means the rank of M is 1. Then the null space of ℝ3 is (3 – rank) = 2-dimensional subspace. So, option A is wrong.
If U is a 2-dimensional subspace of ℝ3, it means the rank of M is 2. Then the null space of ℝ3 is (3 – rank) = 1-dimensional subspace. So, option B is True.
If M is an idempotent matrix, then M2 = M and M3 = M.
Example – M = then M2 is also
So, option C and D is also Correct.
Q50 – Consider the function 𝑓:ℝ→ℝ where ℝ is the set of all real numbers. 𝑓(𝑥) = 𝑥4/4 − 2𝑥3/3 − 3𝑥2/2 + 1
Which of the following statements is/are TRUE?
(A) 𝑥=0 is a local maximum of f
(B) 𝑥=3 is a local minimum of f
(C) 𝑥=−1 is a local maximum of f
(D) 𝑥=0 is a local minimum of f
Ans – (A, B)
Explanation – Polynomial f(x) = 𝑥4/4 − 2𝑥3/3 − 3𝑥2/2 + 1
First Derivative f’(x) = x3 – 2x2 – 3x
- x(x2 – 2x – 3)
- x = 0, x = 3, x = -1
Second Derivative f’’(x) = 3x2 – 4x – 3
- f’’(0) = -3 and -3 < 0 local Maximum of f.
- f’’(3) = 12 and 12 > 0 local Minimum of f.
- f’’(-1) = 4 and 4 > 0 local Minimum of f.
So, option A and B is correct.
Q51 – Consider the directed acyclic graph (DAG) below:

Which of the following is/are valid vertex orderings that can be obtained from a topological sort of the DAG?
(A) P Q R S T U V
(B) P R Q V S U T
(C) P Q R S V U T
(D) P R Q S V T U
Ans – (B, D)
Explanation – Any topological sort must satisfy the following
- P and R before Q
- Q before S and V
- S before U
- V before T
Option (B) and (D) are correct because it follows above rules.
Q52 – Let H, 𝐼, 𝐿, and 𝑁 represent height, number of internal nodes, number of leaf nodes, and the total number of nodes respectively in a rooted binary tree.
Which of the following statements is/are always TRUE?
(A) 𝐿 ≤ 𝐼 + 1
(B) 𝐻+1 ≤ 𝑁 ≤ 2𝐻+1 −1
(C) 𝐻 ≤ 𝐼 ≤ 2𝐻 −1
(D) 𝐻 ≤ 𝐿 ≤ 2𝐻 −1
Ans – (A, B, C)
Explanation – Height = H
Number of Internal nodes = I
Number of Leaf nodes = L
Total number of nodes = N
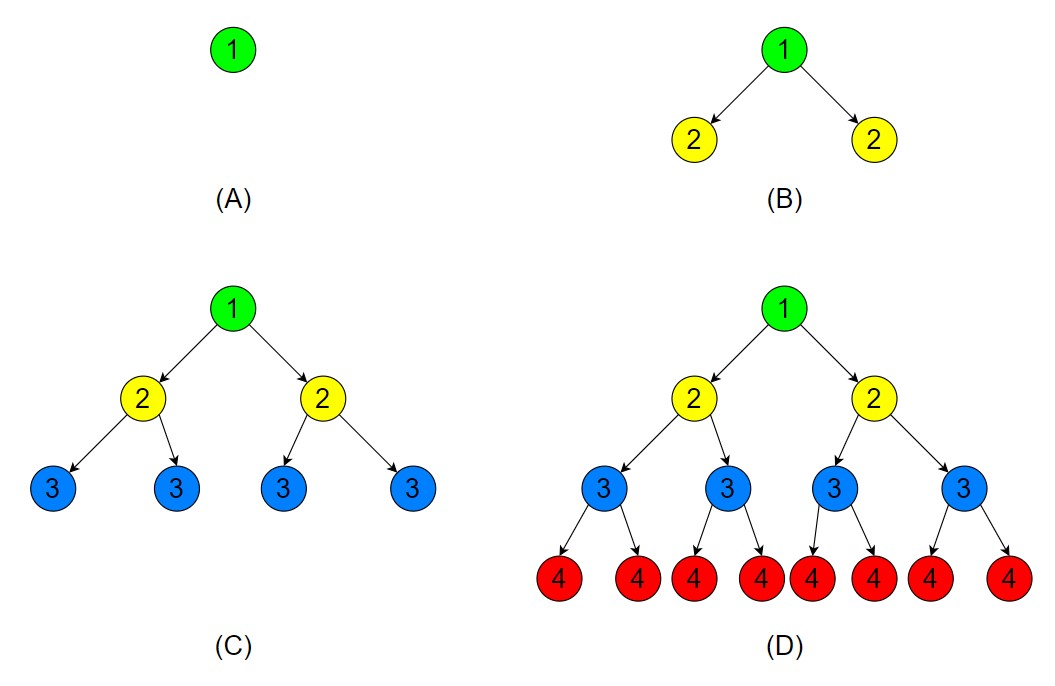
Option A is true, because in a full binary tree L = 𝐼 + 1. Generally, in a binary tree 𝐿 ≤ 𝐼 + 1.
Option B is also true, because in the figure (A) 0+1 ≤ 1 ≤ 20+1 −1 è 1 ≤ 1 ≤ 1
In figure (B) 1+1 ≤ 3 ≤ 21+1 −1 è 2 ≤ 3 ≤ 3
Check figure (C) and (D)?
Option C is also true, because in figure (A) 0 ≤ 0 ≤ 20 −1
Option D is false, because if Height is 3 and number of leaf node is 1 or 2 then H ≤ L is not always true.
Q53 – Consider the following figures representing datasets consisting of two-dimensional features with two classes denoted by circles and squares.

Which of the following is/are TRUE?
(A) (i) is linearly separable.
(B) (ii) is linearly separable.
(C) (iii) is linearly separable.
(D) (iv) is linearly separable.
Ans – (A, D)
Explanation – Option A – (i) and option D – (iv) are linearly separable because a line can separate the circles and squares.

Q54 – Let game(ball, rugby) be true if the ball is used in rugby and false otherwise.
Let shape(ball, round) be true if the ball is round and false otherwise.
Consider the following logical sentences:
s1: ∀ball ¬ game(ball, rugby) ⟹ shape(ball, round)
s2: ∀ball ¬ shape(ball, round) ⟹ game(ball, rugby)
s3: ∀ball game(ball, rugby) ⟹ ¬ shape(ball, round)
s4: ∀ball shape(ball, round) ⟹ ¬ game(ball, rugby)
Which of the following choices is/are logical representations of the assertion,
“All balls are round except balls used in rugby”?
(A) 𝑠1∧𝑠3
(B) 𝑠1∧𝑠2
(C) 𝑠2∧𝑠3
(D) 𝑠3∧𝑠4
Ans – (A, C)
Explanation – P = game(ball, rugby) Q = shape(ball, round)
(S1) ¬P ⟹ Q
- P V Q
(S2) ¬Q ⟹ P
- Q V P
(S3) P ⟹ ¬Q
- ¬P V ¬Q
(S4) Q ⟹ ¬P
- ¬Q V ¬P
The statement – “All balls are round except balls used in rugby”
- (Q ⟹ ¬P) Λ (¬P ⟹ Q)
- (¬Q V ¬P) Λ (P V Q)
Option A – S1ΛS3
- (P V Q) Λ (¬P V ¬Q) Correct.
Option B – S1ΛS2
- (P V Q) Λ (Q V P) Not Correct.
Option C – S2ΛS3
- (Q V P) Λ (¬P V ¬Q) Correct.
Option D – S3ΛS4
- (¬P V ¬Q) Λ (¬Q V ¬P) Not Correct.
Q55 – An OTT company is maintaining a large disk-based relational database of different movies with the following schema:
Movie(ID, CustomerRating)
Genre(ID, Name)
Movie_Genre(MovieID, GenreID)
Consider the following SQL query on the relation database above:
SELECT *
FROM Movie, Genre, Movie_Genre
WHERE
Movie.CustomerRating > 3.4 AND
Genre.Name = “Comedy” AND
Movie_Genre.MovieID = Movie.ID AND
Movie_Genre.GenreID = Genre.ID;
This SQL query can be sped up using which of the following indexing options?
(A) B+ tree on all the attributes.
(B) Hash index on Genre.Name and B+ tree on the remaining attributes.
(C) Hash index on Movie.CustomerRating and B+ tree on the remaining attributes.
(D) Hash index on all the attributes.
Ans – (A, B)
Explanation – Option A – B+ Trees are sorted and it is useful for both selection and join operations. Hence this option speeds up the process.
Option B – The time complexity of Hash index for finding the Genre.Name = “Comedy” is very low. Also, B+ Trees for remaining attributes is good. So, this option speeds up the process.
Option C and D – Hash index can’t support range queries such as (>3.4). So, this option does not speed up the process.
Q56 – Let 𝑋 be a random variable uniformly distributed in the interval [1, 3] and 𝑌 be a random variable uniformly distributed in the interval [2, 4]. If X and Y are independent of each other, the probability P(𝑋≥𝑌) is ______ (rounded off to three decimal places).
Ans – (0.125)
Explanation – Plot X on the x-axis from 1 to 3.
Plot Y on the y-axis from 2 to 4.
This will form a rectangle.

Now we generate a line x = y and mark the region where x ≥ y. This will form a right-angled triangle in the rectangle.
Area of triangle = ½*1*1 = 0.5
Then probability P(𝑋≥𝑌) is 0.5/Total Area = 0.5/4 = 0.125
Q57 – Let 𝑋 be a random variable exponentially distributed with parameter 𝜆 > 0. The probability density function of X is given by:

If 5𝐸(𝑋) = 𝑉𝑎𝑟(𝑋), where 𝐸(𝑋) and 𝑉𝑎𝑟(𝑋) indicate the expectation and variance of 𝑋, respectively, the value of 𝜆 is ______ (rounded off to one decimal place).
Ans – (0.2)
Explanation – E(X) = 1/ 𝜆
Var(x) = 1/ 𝜆2
If 5.E(X) = Var(X),
Then 5.(1/𝜆) = (1/ 𝜆2)
=> 𝜆 = 0.2
Q58 – Consider two events T and S. Let 𝑇’ denote the complement of the event T. The probability associated with different events are given as follows: 𝑃(𝑇’)=0.6, 𝑃(𝑆|𝑇)=0.3, 𝑃(𝑆|𝑇‘)=0.6
Then, 𝑃(𝑇|𝑆) is ______ (rounded off to two decimal places).
Ans – (0.25)
Explanation – P(T|S) = (P(S|T)*P(T)) / P(S)
P(T|S) = 0.3*(1 – P(T’)) / [ P(S∣T)*P(T) + P(S∣T′)*P(T′) ]
P(T|S) = (0.3*0.4) / [ 0.3*0.4 + 0.6*0.6 ]
P(T|S) = 0.12 / 0.48 = 0.25
Q59 – Consider a joint probability density function of two random variables X and Y

Then, 𝐸[𝑌|𝑋=1.5] is ______.
Ans – (1)
Explanation –
Q60 – Evaluate the following limit:

Ans – (0.5)
Explanation – 
Q61 – Let 𝒖 = [ 1; 2; 3; 4; 5] , and let 𝜎1, 𝜎2, 𝜎3, 𝜎4, 𝜎5 be the singular values of the matrix 𝑴= 𝒖𝒖𝑻 (where 𝒖𝑻 is the transpose of 𝒖). The value of Σ5i=1 𝜎i is ______.
Ans – (55)
Explanation – Σ5i=1 𝜎i is the sum of the singular values of matrix M.
M = 5*5 symmetric matrix and of rank 1.
M = 𝒖𝒖𝑻 = Σ5i=1 𝜎i = 12 + 22 + 32 + 42 + 52 = 55.
Q62 – Details of ten international cricket games between two teams “Green” and “Blue” are given in Table C. This table consists of matches played on different pitches, across formats along with their winners. The attribute Pitch can take one of two values: spin-friendly (represented as 𝑆) or pace-friendly (represented as 𝐹). The attribute Format can take one of two values: one-day match (represented as 𝑂) or test match (represented as 𝑇).
A cricket organization would like to use the information given in Table C to develop a decision-tree model to predict outcomes of future games between these two teams.
To develop such a model, the computed InformationGain(C, Pitch) with respect to the Target is ______ (rounded off to two decimal places).
Table C Match Number | Pitch | Format | Winner (Target) |
1 | 𝑆 | 𝑇 | Green |
2 | 𝑆 | 𝑇 | Blue |
3 | 𝐹 | 𝑂 | Blue |
4 | 𝑆 | 𝑂 | Blue |
5 | 𝐹 | 𝑇 | Green |
6 | 𝐹 | 𝑂 | Blue |
7 | 𝑆 | 𝑂 | Green |
8 | 𝐹 | 𝑇 | Blue |
9 | 𝐹 | 𝑂 | Blue |
10 | 𝑆 | 𝑂 | Green |
Ans – (0.12 to 0.13)
Explanation –
Entropy of Winner
Total Events =10
P(Green) = 4/10
P(Blue) = 6/10
Entropy = -[4/10*log2(4/10) + 6/10*log2(6/10)] = 0.971
Entropy of Pitch
Total Events for Spin = 5
P(Green) = 3/5
P(Blue) = 2/5
Entropy = -[3/5*log2(3/5) + 2/5*log2(2/5)] = 0.971
Total Events for Pace = 5
P(Green) = 1/5
P(Blue) = 4/5
Entropy = -[3/5*log2(3/5) + 2/5*log2(2/5)] = 0.721
Weighted Entropy = Probability of Events of Spin*Entropy of Spin + Probability of Events of Pace*Entropy of Pace
Weighted Entropy = (5/10)*0.971 + (5/10)*0.721 = 0.846
Information Gain = Entropy of winner – weighted entropy = 0.971 – 0.846 = 0.125
Rounded of to two decimal places = 0.12
Q63 – Given the two-dimensional dataset consisting of 5 data points from two classes (circles and squares) and assume that the Euclidean distance is used to measure the distance between two points. The minimum odd value of 𝑘 in 𝑘-nearest neighbor algorithm for which the diamond (⋄) shaped data point is assigned the label square is ______.

Ans – (5)
Explanation – The minimum odd value of k in k-nearest neighbor.
When k = 1 (odd number), you look at the 1 closest point to the diamond. There is circle and the diamond will take the same label (circle or square) as this one nearest point.
So, diamond will be circle if k = 1.
When k = 3 (odd number), you look at the 3 closest point to the diamond. There are 2 circle and one square and the diamond will take the same label (whichever is more).
So, diamond will be circle if k = 3.
When k = 5 (odd number), you look at the 5 closest point to the diamond. There are 2 circle and 3 squares and the diamond will take the same label (whichever is more).
So, diamond will be a square if k = 5.
Hence, 5 is the answer.
Q64 – Given the following Bayesian Network consisting of four Bernoulli random variables and the associated conditional probability tables:

The value of 𝑃(𝑈=1, 𝑉=1, 𝑊=1, 𝑍=1) = ______ (rounded off to three decimal places).
Ans – (0.125)
Explanation – 4 Bernoulli random variables U → V, U → W, V → Z, W → Z
We have to find P(U=1,V=1,W=1,Z=1)
From the tables
P(U=1) = 0.5
P(V=1∣U=1) = 0.5
P(W=1∣U=1) = 1
P(Z=1∣V=1,W=1) = 0.5
P(U=1,V=1,W=1,Z=1) = 0.5*0.5*1*0.5 = 0.125
Q65 – Two fair coins are tossed independently. X is a random variable that takes a value of 1 if both tosses are heads and 0 otherwise. Y is a random variable that takes a value of 1 if at least one of the tosses is heads and 0 otherwise.
The value of the covariance of X and Y is ______ (rounded off to three decimal places).
Ans – (0.062 to 0.063)
Explanation –
Event | Probability | X | Y |
HH | 1/4 | 1 | 1 |
HT | 1/4 | 0 | 1 |
TH | 1/4 | 0 | 1 |
TT | 1/4 | 0 | 0 |
Expected Value of X = ¼
Expected Value of Y = ¾
Expected Value of XY (when X = 1 & Y = 1) = ¼
Covariance of X and Y = Expected Value of XY – (Expected Value of X)(Expected Value of Y)
Covariance of X and Y = 1/4 – (1/4*3/4) = 1/16 = 0.063.






 Which ONE of the following statements is TRUE?
Which ONE of the following statements is TRUE?