SYLLABUS
Searching, sorting, hashing. Asymptotic worst case time and space complexity. Algorithm design techniques: greedy, dynamic programming and divide‐and‐conquer. Graph traversals, minimum spanning trees, shortest paths
Q1 – Given an integer array of size N, we want to check if the array is sorted (in either ascending or descending order). An algorithm solves this problem by making a single pass through the array and comparing each element of the array only with its adjacent elements.
The worst-case time complexity of this algorithm is
(A) both Ο(𝑁) and Ω(𝑁)
(B) Ο(𝑁) but not Ω(𝑁)
(C) Ω(𝑁) but not Ο(𝑁)
(D) neither Ο(𝑁) nor Ω(𝑁)
Ans – (A)
Explanation – We are given an array of integers of size N, and we need to see whether it is sorted in ascending or descending order.
The algorithm will do this while only having to compare each element with the element next to it, in one pass through the array.
In the worst-case scenario, we will have to compare each adjacent pair to determine if the array is sorted. This means we will have to do around N−1 comparisons, or O(N). Since in the best case, or worst case, we still will need to check every element once (we can’t skip the element to compare to) when comparing adjacent elements, it is also Ω(N).
Hence, the option A is the answer.
Q2 – The number of spanning trees in a complete graph of 4 vertices labelled A, B, C, and D is _________.
Ans – (16)
Explanation – To find the number of spanning trees in a complete graph with n vertices, we use Cayley’s formula.
For a complete graph with n vertices, the number of spanning trees is nn-2.
For n = 4, the number of spanning trees is 44-2 = 16.
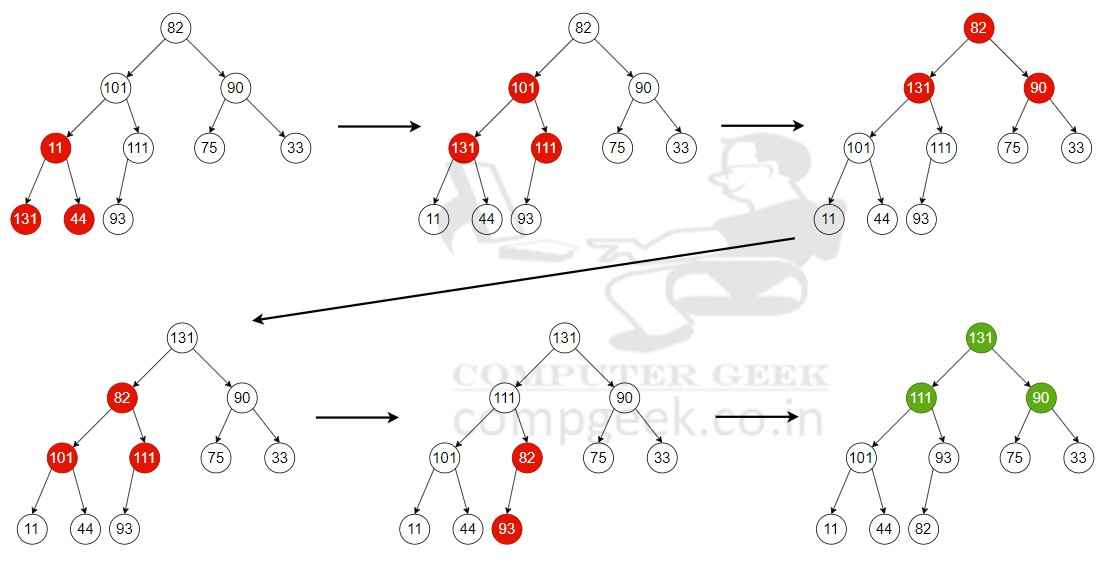
Q3 – An array [82, 101, 90, 11, 111, 75, 33, 131, 44, 93] is heapified. Which one of the following options represents the first three elements in the heapified array?
(A) 82, 90, 101
(B) 82, 11, 93
(C) 131, 11, 93
(D) 131, 111, 90
Ans – (D)
Explanation – Heapifying an array is the act of transforming an array into a heap data type (either a max- or min-heap).
In a given max-heap, for each parent node, the value of each parent node is greater than or equal to the value of each of its children. The last non-leaf node is computed from the last element in the array, moving up toward element one in the array. Processing each parent node upward fixes the heap property of the nodes held to ensure a valid heap property.
Q4 – Consider the following recurrence relation:
𝑇(𝑛) = {√𝑛𝑇(√𝑛) + 𝑛 for 𝑛≥1,
𝑇(𝑛) = {1 for 𝑛=1.
Which one of the following options is CORRECT?
(A) 𝑇(𝑛)= Θ(𝑛 loglog𝑛)
(B) 𝑇(𝑛)=Θ(𝑛 log𝑛)
(C) 𝑇(𝑛)=Θ(𝑛2 log𝑛)
(D) 𝑇(𝑛)=Θ(𝑛2 loglog𝑛)
Ans – (A)
Explanation –
Q5 – Consider a binary min-heap containing 105 distinct elements. Let 𝑘 be the index (in the underlying array) of the maximum element stored in the heap. The number of possible values of 𝑘 is
(A) 53
(B) 52
(C) 27
(D) 1
Ans – (A)
Explanation – In this question, we are finding leaf nodes because maximum elements are stored in the leaf node as this is a min – heap.
In min-heap, the minimum element is always the root and maximum elements cover up the leaf nodes.
The leaf node in an n element heap = n – ⎣n/2⎦
= 105 – ⎣105/2⎦
= 105 – 52 = 53
Hence, number of possible values of k = 53.
Q6 – Let 𝐺 be a directed graph and 𝑇 a depth first search (DFS) spanning tree in 𝐺 that is rooted at a vertex 𝑣. Suppose 𝑇 is also a breadth first search (BFS) tree in 𝐺, rooted at 𝑣.
Which of the following statements is/are TRUE for every such graph 𝐺 and tree 𝑇 ?
(A) There are no back-edges in 𝐺 with respect to the tree 𝑇
(B) There are no cross-edges in 𝐺 with respect to the tree 𝑇
(C) There are no forward-edges in 𝐺 with respect to the tree 𝑇
(D) The only edges in 𝐺 are the edges in 𝑇
Ans – (C)
Explanation – We have given a directed graph G and a spanning tree T which was formed from both a Depth First Search (DFS) and a Breadth First Search (BFS) with respect to the same root vertex v.
In DFS, you will find edges in the directed graph G being defined as any of the following – tree edges, back edges, forward edges, or cross edges.
When a tree is a BFS-tree, the vertex is visited in what is known as levels. Thus, in one level you will find child vertices and in the next level the grandchildren, and so on. Hence, a forward edge from a parent vertex to any granddaughter vertex will violate the level structure of the BFS search, which means there could not be any forward edges with respect to tree T. Therefore, the only correct option is (C).
Q7 – The chromatic number of a graph is the minimum number of colours used in a proper colouring of the graph. Let 𝐺 be any graph with 𝑛 vertices and chromatic number 𝑘.
Which of the following statements is/are always TRUE?
(A) 𝐺 contains a complete subgraph with 𝑘 vertices
(B) 𝐺 contains an independent set of size at least 𝑛/𝑘
(C) 𝐺 contains at least 𝑘(𝑘−1)/2 edges
(D) 𝐺 contains a vertex of degree at least 𝑘
Ans – (B, C)
Explanation – Even though a graph requires k colors to color it, it does not imply that it must have a complete subgraph k. For example, certain graphs, such as the Mycielskian graphs, have high chromatic numbers, but do not have large complete subgraphs. So, option A is not necessarily true.
In any proper coloring with k colors, the vertices are divided into k color classes. Each color class is an independent set. By the pigeonhole principle, at least one of the color classes must have size ≥⌈n/k⌉, thus at least n/k. So, option B is necessarily true.
The minimal number of edges of such a graph is at least k(k−1)/2.This bound is from the extremal example – a complete graph on k vertices, which is the smallest graph with chromatic number k. Thus, in chromatic number k, at least k(k−1)/2 edges are required. So, option C is necessarily true.
A graph can exhibit chromatic number k, but all degree less than k. Thus, we will again turn to examples of Mycielski graphs – vertices can be triangle-free, hence no high degree vertices, but nevertheless require more colors. So, option D is not necessarily true.
Q8 – The number of edges present in the forest generated by the DFS traversal of an undirected graph 𝐺 with 100 vertices is 40. The number of connected components in 𝐺 is _________.
Ans – (60)
Explanation – In a DFS forest, each tree represents one connected component. A tree with n vertices has exactly n – 1 edges.
Now, suppose the number of connected components is k.
- Each of those k trees contributes nᵢ – 1 edges.
Total number of edges in all trees => ∑(ni – 1) = 100 – k
=> 40 = 100 – k
Then, k = 60


