Understanding the Floyd-Warshall Algorithm
.
Definition
The Floyd-Warshall algorithm is a dynamic programming technique used to find the shortest paths between all pairs of vertices in a weighted graph.
Unlike other shortest path algorithms, such as Dijkstra’s algorithm, which focuses on finding the shortest path from one source vertex to all other vertices, the Floyd-Warshall algorithm computes the shortest paths between every pair of vertices in the graph.
It can handle graphs with both positive and negative edge weights (as long as there are no negative cycles).
The algorithm works by iteratively considering all vertices as potential intermediate points in paths between every pair of vertices, updating the shortest path distances accordingly until the shortest paths between all pairs of vertices are determined.
.
History
The Floyd-Warshall algorithm, named after Robert Floyd and Stephen Warshall, is a significant development in the field of computer science and graph theory for solving the all-pairs shortest path problem on graphs.
Stephen Warshall (1962) – The earliest form of the algorithm was presented by Stephen Warshall in 1962. Warshall’s original intent was to develop an efficient algorithm for computing the transitive closure of a directed graph. His algorithm was primarily aimed at determining reachability, that is, finding whether there is a path from each vertex in a graph to every other vertex.
Robert Floyd (1962) – Independently of Warshall, Robert Floyd developed a similar algorithm for finding the shortest paths in a weighted graph. Floyd’s work was more general in that it extended Warshall’s idea from binary reachability to handling varying weights associated with graph edges.
.
How It Works
The Floyd-Warshall algorithm operates by iteratively improving the solution until it covers all pairs of vertices. It does this by considering each vertex as an intermediate point in the path between two other vertices.
.
Algorithm
function FloydWarshall(Graph, V)
Let dist = array of dimensions [V][V]
Step 1 – Initialize the distance matrix
for i from 1 to V
for j from 1 to V:
if i == j
dist[i][j] = 0
else if there is an edge from i to j
dist[i][j] = weight of edge from i to j
else
dist[i][j] = ∞
Step 2 – Algorithm main loop
for k from 1 to V
for i from 1 to V
for j from 1 to V
if ( dist[i][k] + dist[k][j] < dist[i][j] )
dist[i][j] = dist[i][k] + dist[k][j]
return dist
.
Example
Let’s consider a practical example of the Floyd-Warshall algorithm applied to a simple road network between houses. This example will illustrate how you can use the algorithm to determine the shortest paths between each pair of houses.
Imagine a small community with five houses, labelled A, B, C, D, and E. The roads between them have different lengths, and not all houses are directly connected by roads.

Here is the adjacency matrix.

Diagonal is 0, because the shortest distance from any vertex to itself is 0.
.
Step 1 – Using house A as an intermediate node 𝑘 = 0, Update the matrix by checking if a path through A gives a shorter route between any two houses.
In the adjacency matrix, the A’s row, A’s column and diagonal remain as it is.
dist[B][C] = min(dist[B][C], dist[B][A] + dist[A][C])
dist[B][C] = min (BC, BA + AC) = min (∞, ∞ + 8) = ∞
So, we will apply same formula in rest of the cells.
dist[B][D] = min (BD, BA + AD) = min (1, ∞ + ∞) = 1
dist[B][E] = min (BE, BA + AE) = min (7, ∞ + (- 4)) = 7
dist[C][B] = min (CB, CA + AB) = min (4, ∞ + 3) = 4
dist[C][D] = min (CD, CA + AD) = min (∞, ∞ + ∞) = ∞
dist[C][E] = min (CE, CA + AE) = min (∞, ∞ + (- 4)) = ∞
dist[D][B] = min (DB, DA + AB) = min (∞, 2 + 3) = 5, Changed to minimum.
dist[D][C] = min (DC, DA + AC) = min (-5, 2 + 8) = -5
dist[D][E] = min (DE, DA + AE) = min (∞, 2 + (-4)) = -2, Changed to minimum.
dist[E][B] = min (EB, EA + AB) = min (∞, ∞ + 3) = ∞
dist[E][C] = min (EC, EA + AC) = min (∞, ∞ + 8) = ∞
dist[E][D] = min (ED, EA + AD) = min (6, ∞ + ∞) = 6.
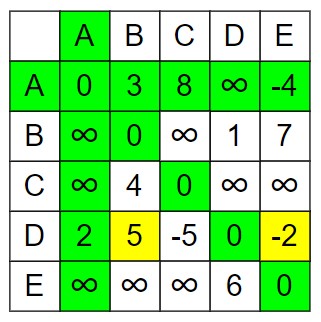
Step 2 – Using house B as an intermediate node 𝑘 = 0, Update the matrix by checking if a path through B gives a shorter route between any two houses.
In the adjacency matrix, the B’s row, B’s column and diagonal remain as it is.
dist[A][C] = min (AC, AB + BC) = min (8, 3 + ∞) = 8
dist[A][D] = min (AD, AB + BD) = min (∞, 3 + 1) = 4, Changed to minimum.
dist[A][E] = min (AE, AB + BE) = min (-4, 3 + 7) = -4
dist[C][A] = min (CA, CB + BA) = min (∞, 4 + ∞) = ∞
dist[C][D] = min (CD, CB + BD) = min (∞, 4 + 1) = 5, Changed to minimum.
dist[C][E] = min (CE, CB + BE) = min (∞, 4 + 7) = 11, Changed to minimum.
dist[D][A] = min (DA, DB + BA) = min (2, 5 + ∞) = 2
dist[D][C] = min (DC, DB + BC) = min (-5, 5 + ∞) = -5
dist[D][E] = min (DE, DB + BE) = min (-2, 5 + 7) = -2
dist[E][A] = min (EA, EB + BA) = min (∞, ∞ + ∞) = ∞
dist[E][C] = min (EC, EB + BC) = min (∞, ∞ + ∞) = ∞.
dist[E][D] = min (ED, EB + BD) = min (6, ∞ + 1) = 6.
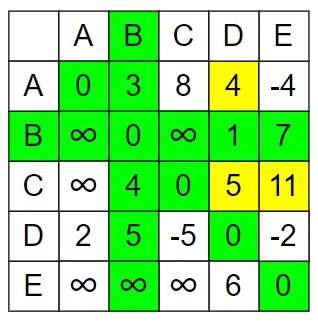
Step 3 – Using house C as an intermediate node 𝑘 = 0, Update the matrix by checking if a path through C gives a shorter route between any two houses.
In the adjacency matrix, the C’s row, C’s column and diagonal remain as it is.
dist[A][B] = min (AB, AC + CB) = min (3, 8 + 4) = 3
dist[A][D] = min (AD, AC + CD) = min (4, 8 + 5) = 4
dist[A][E] = min (AE, AC + CE) = min (-4, 8 + 11) = -4
dist[B][A] = min (BA, BC + CA) = min (∞, ∞ + ∞) = ∞
dist[B][D] = min (BD, BC + CD) = min (1, ∞ + 5) = 1
dist[B][E] = min (BE, BC + CE) = min (7, ∞ + 11) = 7
dist[D][A] = min (DA, DC + CA) = min (2, -5 + ∞) = 2
dist[D][B] = min (DB, DC + CB) = min (5, -5 + 4) = -1, Changed to minimum.
dist[D][E] = min (DE, DC + CE) = min (-2, -5 + 11) = -2
dist[E][A] = min (EA, EC + CA) = min (∞, ∞ + ∞) = ∞
dist[E][B] = min (EB, EC + CB) = min (∞, ∞ + 4) = ∞.
dist[E][D] = min (ED, EC + CD) = min (6, ∞ + 5) = 6.

Step 4 – Using house D as an intermediate node 𝑘 = 0, Update the matrix by checking if a path through D gives a shorter route between any two houses.
In the adjacency matrix, the D’s row, D’s column and diagonal remain as it is.
dist[A][B] = min (AB, AD + DB) = min (3, 4 + (-1)) = 3
dist[A][C] = min (AC, AD + DC) = min (4, 4 + (-5)) = -1, Changed to minimum.
dist[A][E] = min (AE, AD + DE) = min (-4, 4 + (-2)) = -4
dist[B][A] = min (BA, BD + DA) = min (∞, 1 + 2) = 3, Changed to minimum.
dist[B][C] = min (BC, BD + DC) = min (∞, 1 + (-5)) = -4, Changed to minimum.
dist[B][E] = min (BE, BD + DE) = min (7, 1 + (-2)) = -1, Changed to minimum.
dist[C][A] = min (CA, CD + DA) = min (∞, 5 + 2) = 7, Changed to minimum.
dist[C][B] = min (CB, CD + DB) = min (4, 5 + (-1)) = 4
dist[C][E] = min (CE, CD + DE) = min (11, 5 + (-2)) = 3, Changed to minimum.
dist[E][A] = min (EA, ED + DA) = min (∞, 6 + 2) = 8, Changed to minimum.
dist[E][B] = min (EB, ED + DB) = min (∞, 6 + (-1)) = 5, Changed to minimum.
dist[E][C] = min (EC, ED + DC) = min (∞, 6 + (-5)) = 1.

Step 5 – Using house E as an intermediate node 𝑘 = 0, Update the matrix by checking if a path through E gives a shorter route between any two houses.
In the adjacency matrix, the E’s row, E’s column and diagonal remain as it is.
dist[A][B] = min (AB, AE + EB) = min (3, -4 + 5) = 1, Changed to minimum.
dist[A][C] = min (AC, AE + EC) = min (-1, -4 + 1) = -3, Changed to minimum.
dist[A][D] = min (AD, AE + ED) = min (4, -4 + 6) = 2, Changed to minimum.
dist[B][A] = min (BA, BE + EA) = min (3, -1 + 8) = 3
dist[B][C] = min (BC, BE + EC) = min (-4, -1 + 1) = -4
dist[B][D] = min (BD, BE + ED) = min (1, -1 + 6) = 1
dist[C][A] = min (CA, CE + EA) = min (7, 3 + 8) = 7
dist[C][B] = min (CB, CE + EB) = min (4, 3 + 5) = 4
dist[C][D] = min (CD, CE + ED) = min (5, 3 + 6) = 5
dist[D][A] = min (DA, DE + EA) = min (2, -2 + 8) = 2
dist[D][B] = min (DB, DE + EB) = min (-1, -2 + 5) = -1
dist[D][C] = min (DC, DE + EC) = min (-5, -2 + 1) = -5.
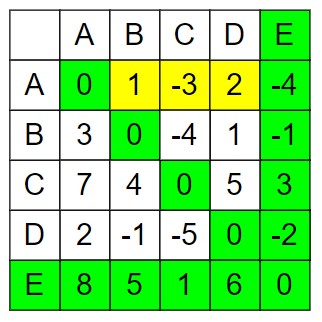
.
Source Code of Floyd-Warshall Algorithm
// COMPUTER GEEK – compgeek.co.in
// Write a program for Floyd Warshall Algorithm
#include <stdio.h>
#include <limits.h> // For INT_MAX
#define MAX_VERTICES 100
void printMatrix(int dist[][MAX_VERTICES], int V);
int main() {
int V, E; // Number of vertices and edges
int graph[MAX_VERTICES][MAX_VERTICES];
int i, j, k;
int u, v, w; // Variables to store the edge (u, v) and weight w
printf(“Enter the number of vertices: “);
scanf(“%d”, &V);
printf(“Enter the number of edges: “);
scanf(“%d”, &E);
// Initialize the graph with infinity (no direct path)
for (i = 0; i < V; i++) {
for (j = 0; j < V; j++) {
if (i == j)
graph[i][j] = 0; // Distance to itself is 0
else
graph[i][j] = INT_MAX;
}
}
// Read the edges and their weights
printf(“Enter the edges and weights (u v w):\n”);
for (i = 0; i < E; i++) {
scanf(“%d %d %d”, &u, &v, &w);
graph[u][v] = w;
}
// Floyd-Warshall Algorithm
for (k = 0; k < V; k++) {
for (i = 0; i < V; i++) {
for (j = 0; j < V; j++) {
if (graph[i][k] != INT_MAX && graph[k][j] != INT_MAX && graph[i][j] > graph[i][k] + graph[k][j]) {
graph[i][j] = graph[i][k] + graph[k][j];
}
}
}
}
// Print the shortest path matrix
printf(“The matrix of shortest paths between every pair of vertices:\n”);
printMatrix(graph, V);
return 0;
}
void printMatrix(int dist[][MAX_VERTICES], int V) {
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (dist[i][j] == INT_MAX)
printf(“INF “);
else
printf(“%d “, dist[i][j]);
}
printf(“\n”);
}
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Floyd Warshall Algorithm
#include <iostream>
#include <vector>
#include <climits> // For INT_MAX
using namespace std;
void printMatrix(const vector<vector<int>>& dist, int V);
int main() {
int V, E;
cout << “Enter the number of vertices: “;
cin >> V;
cout << “Enter the number of edges: “;
cin >> E;
vector<vector<int>> graph(V, vector<int>(V, INT_MAX));
// Initialize distances to self as 0
for (int i = 0; i < V; ++i)
graph[i][i] = 0;
cout << “Enter the edges and weights (u v w):\n”;
int u, v, w;
for (int i = 0; i < E; ++i) {
cin >> u >> v >> w;
graph[u][v] = w;
}
// Floyd-Warshall Algorithm
for (int k = 0; k < V; ++k) {
for (int i = 0; i < V; ++i) {
for (int j = 0; j < V; ++j) {
if (graph[i][k] != INT_MAX && graph[k][j] != INT_MAX && graph[i][j] > graph[i][k] + graph[k][j]) {
graph[i][j] = graph[i][k] + graph[k][j];
}
}
}
}
// Printing the result
cout << “The matrix of shortest paths between every pair of vertices:\n”;
printMatrix(graph, V);
return 0;
}
void printMatrix(const vector<vector<int>>& dist, int V) {
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (dist[i][j] == INT_MAX)
cout << “INF “;
else
cout << dist[i][j] << ” “;
}
cout << endl;
}
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Floyd Warshall Algorithm
import java.util.Scanner;
import java.util.Arrays;
public class FloydWarshall {
private static final int INF = Integer.MAX_VALUE;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println(“Enter the number of vertices:”);
int V = scanner.nextInt();
System.out.println(“Enter the number of edges:”);
int E = scanner.nextInt();
int[][] graph = new int[V][V];
for (int[] row : graph) {
Arrays.fill(row, INF);
}
for (int i = 0; i < V; i++) {
graph[i][i] = 0;
}
System.out.println(“Enter the edges and weights (u v w):”);
for (int i = 0; i < E; i++) {
int u = scanner.nextInt();
int v = scanner.nextInt();
int w = scanner.nextInt();
graph[u][v] = w;
}
// Floyd-Warshall Algorithm
for (int k = 0; k < V; k++) {
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (graph[i][k] != INF && graph[k][j] != INF && graph[i][j] > graph[i][k] + graph[k][j]) {
graph[i][j] = graph[i][k] + graph[k][j];
}
}
}
}
// Print the shortest path matrix
System.out.println(“The matrix of shortest paths between every pair of vertices:”);
printMatrix(graph, V);
}
private static void printMatrix(int[][] dist, int V) {
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (dist[i][j] == INF)
System.out.print(“INF “);
else
System.out.print(dist[i][j] + ” “);
}
System.out.println();
}
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for Floyd Warshall Algorithm
def floyd_warshall(vertices, edges):
# Initialize distance array
inf = float(‘inf’)
dist = [[inf] * vertices for _ in range(vertices)]
for i in range(vertices):
dist[i][i] = 0
for u, v, w in edges:
dist[u][v] = w
# Floyd-Warshall algorithm
for k in range(vertices):
for i in range(vertices):
for j in range(vertices):
if dist[i][k] != inf and dist[k][j] != inf and dist[i][j] > dist[i][k] + dist[k][j]:
dist[i][j] = dist[i][k] + dist[k][j]
return dist
def main():
vertices = int(input(“Enter the number of vertices: “))
num_edges = int(input(“Enter the number of edges: “))
edges = []
print(“Enter the edges and weights (u v w):”)
for _ in range(num_edges):
u, v, w = map(int, input().split())
edges.append((u, v, w))
distances = floyd_warshall(vertices, edges)
print(“The matrix of shortest paths between every pair of vertices:”)
for row in distances:
print(” “.join(map(lambda x: ‘inf’ if x == float(‘inf’) else str(x), row)))
if __name__ == “__main__”:
main()
Enter the number of vertices: 5
Enter the number of edges: 9
Enter the edges and weights (u v w):
0 1 3
0 2 8
0 4 -4
1 3 1
1 4 7
2 1 4
3 0 2
3 2 -5
4 3 6
The matrix of shortest paths between every pair of vertices:
0 1 -3 2 -4
3 0 -4 1 -1
7 4 0 5 3
2 -1 -5 0 -2
8 5 1 6 0
=== Code Execution Successful ===
Time Complexity
In the Floyd-Warshall algorithm, regardless of the individual time complexities of Dijkstra’s, Bellman-Ford, or BFS algorithms, the overall time complexity of Floyd-Warshall remains 𝑂(𝑉3).
Given that each of the three nested loops runs 𝑉 times, the total number of operations performed by the algorithm is proportional to 𝑉×𝑉×𝑉, or 𝑉3. This leads to the overall time complexity 𝑂(𝑉3).
.
Space Complexity
The core of the Floyd-Warshall algorithm involves maintaining a matrix that stores the shortest path distances between all pairs of vertices. This matrix, typically denoted as dist[i][j], represents the shortest distance from vertex i to vertex j.
The auxiliary space outside of the distance matrix is 𝑂(1), as these variables occupy constant space.
Since dist[i][j] matrix is a two-dimensional array with dimensions equivalent to the number of vertices (V) in the graph, the space required to store this matrix is proportional to 𝑉2. Specifically, every cell in the 𝑉×𝑉 matrix needs to be stored, so the space complexity is 𝑂(𝑉2).
.
Applications
- A delivery service can use the algorithm to find the quickest or shortest paths for multiple deliveries within a city, ensuring efficient route planning for drivers.
- Internet service providers might use it to determine the best path for data to travel across network nodes, enhancing speed and service reliability for users.
- A social media platform could use it to suggest new friends by identifying users who are within a small number of connection paths but not directly connected (mutual friends).
- Automated guided vehicles (AGVs) in a warehouse can use the algorithm to find the most efficient route to collect and deliver goods, minimizing travel time and avoiding bottlenecks.
- Planning the routes for public transportation to ensure they connect densely populated areas with major points of interest like malls, hospitals, and schools effectively.
- In a strategy game, the AI can use the algorithm to plan movements of units across the game map efficiently, reacting to player actions and ensuring competitive gameplay.
- Managing transactions in a banking network by finding the quickest paths for transaction verifications and processing to minimize delays.
Test Yourself
Q1- Why is the Floyd-Warshall algorithm considered a dynamic programming algorithm?
Because it solves the problem by breaking it down into simpler subproblems (shortest paths involving intermediate vertices) and then combining these subproblems in a manner that considers previous computations (using previously calculated shortest paths to update other paths).
Q2- Can the Floyd-Warshall algorithm detect negative weight cycles? If yes, how?
Yes, the Floyd-Warshall algorithm can detect negative weight cycles. After the algorithm runs, if any diagonal element of the distance matrix is negative (i.e., dist[i][i] < 0 for any vertex i), this indicates a negative weight cycle in the graph.
Q3- How can Floyd Warshall algorithm apply on an undirected graph? Give an example.
Example of an Undirected Graph
Let’s consider a small undirected graph with three vertices – A, B, and C.
The edges between them have weights as follows
A – B has a weight of 1
B – C has a weight of 2
A – C has a weight of 4
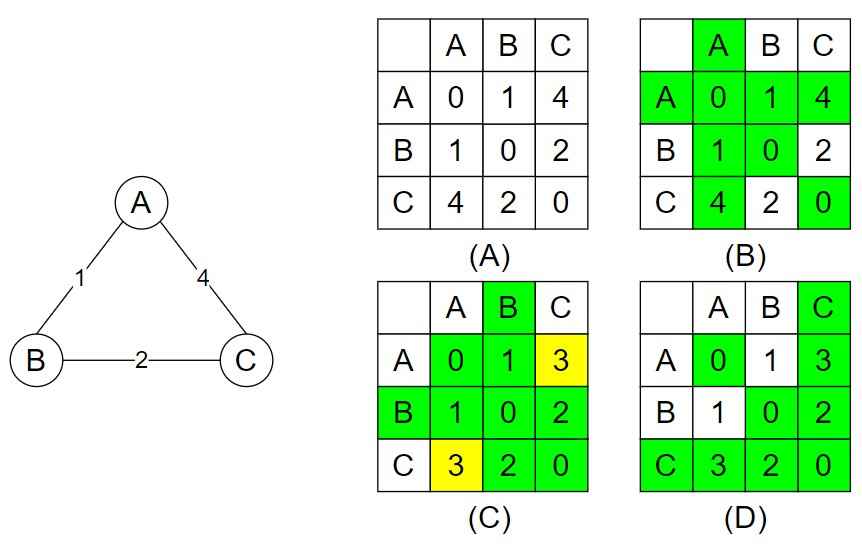
Q4- Why does the Floyd-Warshall algorithm use a triple nested loop?
The triple nested loop in Floyd-Warshall iterates over each vertex as a potential intermediate vertex in the shortest paths between all pairs of other vertices.
This structure ensures that the algorithm systematically updates the shortest paths by considering each vertex’s influence on the paths between every pair of nodes.
Q5- How can the space complexity of Floyd-Warshall be reduced if only the shortest distances are needed?
The space complexity cannot be reduced below O(V2) because you need to store the distances for all pairs of vertices. However, you don’t need additional space beyond this matrix, assuming you only need to know the distances, not the paths.
Q6- Which of the following statements about the Floyd-Warshall algorithm is TRUE?
It can only handle positive weight edges.
It uses a greedy strategy to find the shortest paths.
It can handle negative weight edges but not negative weight cycles.
It is less efficient than Dijkstra’s algorithm for sparse graphs.
Ans – (3)
Explanation – Floyd-Warshall algorithm handles graphs with negative weights effectively unless there are negative cycles.
Q7- Which of the following is a correct initialization for the Floyd-Warshall algorithm’s distance matrix?
Set all off-diagonal elements to 0 and diagonals to ∞.
Set all elements to the edge weights, and non-existent edges to 0.
Set all elements to ∞, except the diagonal elements set to 0.
Set all diagonal elements to 0, and directed edges to edge weights and non-existent edges to ∞.
Ans – (4)
Explanation – The initial distance matrix is set based on the direct distances between nodes (edge weights), with non-existent edges typically set to ∞ and diagonal elements (distances to self) set to 0.
Q8- What type of graph is most suitable for the Floyd-Warshall algorithm?
Unweighted graphs
Graphs with negative weight edges
Dense graphs
Sparse graphs
Ans – (3)
Explanation – While Floyd-Warshall can handle various types of graphs, it is particularly efficient for dense graphs where the number of vertices isn’t excessively large due to its O(V3) time complexity.
Q9- How does the Floyd-Warshall algorithm update distances?
By comparing the existing path with a potentially shorter path through another vertex.
By always choosing the lightest edge available.
By removing edges that do not contribute to the shortest path.
By performing a depth-first search to find the shortest path.
Ans – (1)
Explanation – The core of the Floyd-Warshall algorithm involves updating the distance matrix by considering intermediate vertices that might offer a shorter path between two vertices.
Q10- Which of the following scenarios is an ideal application of the Floyd-Warshall algorithm?
Finding the shortest path in a large sparse graph from a single source
Finding the minimum spanning tree in a weighted graph
Finding the shortest paths between all pairs of vertices in a small to medium-sized graph
Maximizing the flow in a network
Ans – (3)
Explanation – The Floyd-Warshall algorithm is particularly effective for finding shortest paths between all pairs of vertices in small to medium-sized graphs, especially when the graph is dense or has negative weights but no negative cycles.
Q11- Can the Floyd-Warshall algorithm be used to find the shortest paths in a directed acyclic graph (DAG)?
Yes, the algorithm can be used for a DAG, but it is not the most efficient choice.
Since a DAG has no cycles, algorithms like topological sorting combined with dynamic programming are more suitable.






