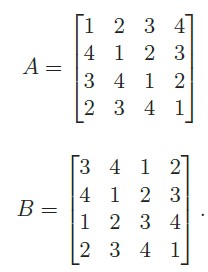Engineering Mathematics Question Answers GATE 2023

Engineering Mathematics GATE Question Answers with Explanation.

Q1 – Let

Let det(A) and det(B) denote the determinants of the matrices A and B, respectively.

Which one of the options given below is TRUE? (GATE 2023)

det(A) = det(B)
det(B) = −det(A)
det(A) = 0
det(AB) = det(A)+det(B)

Ans – (2)

Explanation –

Q2 – Geetha has a conjecture about integers, which is of the form ∀x(P(x)) ⇒ ∃yQ(x, y),

where P is a statement about integers, and Q is a statement about pairs of integers.

Which of the following (one or more) option(s) would imply Geetha’s conjecture? (GATE 2023)

∃x(P(x) ∧ ∀yQ(x, y))
∀x∀yQ(x, y)
∃y∀x(P(x) ⇒ Q(x, y))
∃x(P(x) ∧ ∃yQ(x, y))

Ans – (2, 3)

Explanation –

Q3 – Let f(x) = x³ + 15x² − 33x – 36 be a real-valued function.

Which of the following statements is/are TRUE? (GATE 2023)

f(x) does not have a local maximum.
f(x) has a local maximum.
f(x) does not have a local minimum.
f(x) has a local minimum.

Ans – (2, 4)

Explanation –

Q4 – Let A be the adjacency matrix of the graph with vertices {1, 2, 3, 4, 5}.

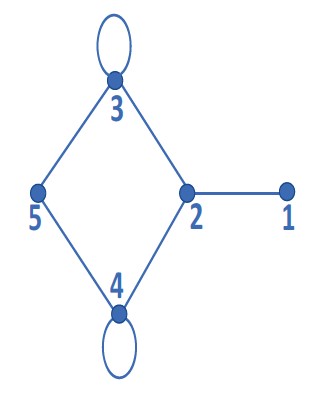
Let λ1, λ2, λ3, λ4, and λ5 be the five eigenvalues of A. Note that these eigenvalues need not be distinct.

The value of λ1 + λ2 + λ3 + λ4 + λ5 = ___________. (GATE 2023)

Ans – (2)

Explanation –

Q5 – The value of the definite integral

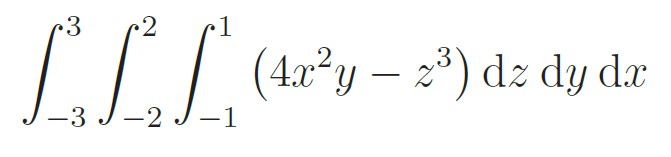
is _________. (Rounded off to the nearest integer) (GATE 2023)

Ans – (0 to 0)

Explanation –

Q6 – A particular number is written as 132 in radix-4 representation. The same number in radix-5 representation is __________. (GATE 2023)

Ans – (110)

Explanation –

Q7 – Let U = {1, 2, . . . , n}, where n is a large positive integer greater than 1000. Let k be a positive integer less than n. Let A, B be subsets of U with |A| = |B| = k

and A ∩ B = ∅. We say that a permutation of U separates A from B if one of the following is true.

– All members of A appear in the permutation before any of the members of B.

– All members of B appear in the permutation before any of the members of A.

How many permutations of U separate A from B? (GATE 2023)

Ans – (4)

Explanation –

Q8 – Let f: A → B be an onto (or surjective) function, where A and B are nonempty sets. Define an equivalence relation ∼ on the set A as

a1 ∼ a2 if f(a1) = f(a2) , where a1, a2 ∈ A.

Let E = {[x] : x ∈ A} be the set of all the equivalence classes under ∼. Define a new mapping F: ε →B as

F([x]) = f(x), for all the equivalence classes [x] in ε.

Which of the following statements is/are TRUE? (GATE 2023)

F is NOT well-defined.
F is an onto (or surjective) function.
F is a one-to-one (or injective) function.
F is a bijective function.

Ans – (2, 3, 4)

Explanation –

Q9 – Let X be a set and 2^X denote the powerset of X.

Define a binary operation Δ on 2^X as follows:

A Δ B = (A − B) ∪ (B − A).

Let H = (2^X, Δ).

Which of the following statements about H is/are correct? (GATE 2023)

H is a group.
Every element in H has an inverse, but H is NOT a group.
For every A ∈ 2^X, the inverse of A is the complement of A.
For every A ∈ 2^X, the inverse of A is A.

Ans – (1, 4)

Explanation –

Q10 – Consider a random experiment where two fair coins are tossed. Let A be the event that denotes HEAD on both the throws, B be the event that denotes HEAD on the first throw, and C be the event that denotes HEAD on the second throw.

Which of the following statements is/are TRUE? (GATE 2023)

A and B are independent.
A and C are independent.
B and C are independent.
Prob(B|C) = Prob(B)

Ans – (3, 4)

Explanation –