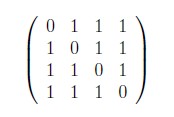Engineering Mathematics Question Answers GATE 2021

Engineering Mathematics GATE Question Answers with Explanation.

Q1 – Let p and q be two propositions. Consider the following two formulae in propositional logic.

S₁: ( ¬p ∧ (p ∨ q)) -> q

S₂: q -> (¬p ∧ (p ∨ q))

Which one of the following choices is correct? (GATE 2021 SET 1)

Both S₁ and S₂ are tautologies.
S₁ is a tautology but S₂ is not a tautology.
S₁ is not a tautology but S₂ is a tautology.
Neither S₁ not S₂ is a tautology.

Ans – (2)

Explanation –

Q2 – The lifetime of a component of a certain type is a random variable whose probability density function is exponentially distributed with parameter 2. For a randomly picked component of this type, the probability that its lifetime exceeds the expected lifetime (rounded to 2 decimal places) is ____________. (GATE 2021 SET 1)

Ans – (0.35 to 0.39)

Explanation –

Q3 – There are 6 jobs with distinct difficulty levels, and 3 computers with distinct processing speeds. Each job is assigned to a computer such that:

– The fastest computer gets the toughest job and the slowest computer gets the easiest job.

– Every computer gets at least one job.

The number of ways in which this can be done is ___________. (GATE 2021 SET 1)

Ans – (65)

Explanation –

Q4 – Consider the following expression.

The value of the above expression (rounded to 2 decimal places) is ___________. (GATE 2021 SET 1)

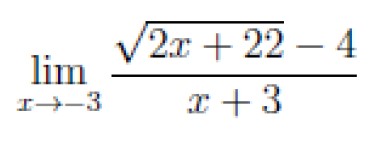
Ans – (0.25)

Explanation –

Q5 – Consider the following representation of a number in IEEE 754 single-precision floating point format with a bias of 127.

S : 1 E : 10000001 F : 11110000000000000000000

Here, S, E and F denote the sign, exponent, and fraction components of the floating-point representation. The decimal value corresponding to the above representation (rounded to 2 decimal places) is ____________. (GATE 2021 SET 1)

Ans – (-7.75)

Explanation –

Q6 – Let G be a group of order 6, and H be a subgroup of G such that 1 <|H|< 6. Which one of the following options is correct? (GATE 2021 SET 1)

Both G and H are always cyclic
G may not be cyclic, but H is always cyclic
G is always cyclic, but H may not be cyclic
Both G and H may not be cyclic

Ans – (2)

Explanation –

Q7 – Consider the two statements.

S1: There exist random variables X and Y such that

S2: For all random variables X and Y,

Which one of the following choices is correct? (GATE 2021 SET 1)

Both S1 and S2 are true
S1 is true, but S2 is false
S1 is false, but S2 is true
Both S1 and S2 are false

Ans – (4)

Explanation –

Q8 – Let G = (V, E) be an undirected unweighted connected graph. The diameter of G is defined as:

Let M be the adjacency matrix of G.

Define graph G2 on the same set of vertices with adjacency matrix N, where

Which one of the following statements is true? (GATE 2021 SET 1)

diam(G2) ≤ ⌈ diam(G)/2⌉
⌈diam(G)/2⌉ < diam(G₂) < diam(G)
diam(G₂) = diam(G)
diam(G) < diam(G₂) ≤ 2 diam(G)

Ans – (1)

Explanation –

Q9 – A relation R is said to be circular if aRb and bRc together imply cRa. Which of the following options is/are correct? (GATE 2021 SET 1)

If a relation S is reflexive and symmetric, then S is an equivalence relation.
If a relation S is circular and symmetric, then S is an equivalence relation.
If a relation S is reflexive and circular, then S is an equivalence relation.
If a relation S is transitive and circular, then S is an equivalence relation.

Ans – (1, 2, 3)

Explanation –

Q10 – Consider the following matrix.

The largest eigenvalue of the above matrix is __________. (GATE 2021 SET 1)

Ans – (3)

Explanation –

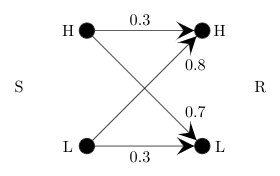
Q11 – A sender (S) transmits a signal, which can be one of the two kinds: H and L with probabilities 0.1 and 0.9 respectively, to a receiver (R).

In the graph below, the weight of edge (u, v) is the probability of receiving v when u is transmitted, where u, v ∈ {H, L}. For example, the probability that the received signal is L given the transmitted signal was H, is 0.7.

If the received signal is H, the probability that the transmitted signal was H (rounded to 2 decimal places) is __________.

Ans – (0.04)

Explanation –