Introduction
.
The Egg Dropping Problem is a classic puzzle in the Design and Analysis of Algorithms. It is often used to demonstrate dynamic programming techniques.
The problem is about finding the minimum number of trials needed to determine the highest step in a building from which an egg can be dropped without breaking, given a certain number of eggs and steps.
.
Problem Statement

“You are given two eggs and a building with n steps. You need to determine the highest step from which you can drop an egg without it breaking, using the fewest number of trials in the worst-case scenario.”
or
“We want the minimum number of trials, needed in the worst case to determine the highest step from which an egg can be dropped without breaking, if we have two eggs.”
Assumptions
- Reusable Eggs: An egg that survives a fall can be reused.
- Broken Eggs Removed: A broken egg should be removed from further trials.
- Uniform Reaction: Every egg experiences the same reaction when it falls.
- Higher Step Breaks: If an egg breaks from a certain step, it will also break from any higher step.
- Lower Step Survival: If an egg survives a fall, it will also survive a fall from any lower step.
- Edge Cases: It is possible that the egg may break from the first step, and it may also survive a fall from the nth step.
.
To find the answer, let’s explore a couple of basic methods
- Linear Search Method
This is the simplest approach where you start dropping the egg from the first step and move upwards until the egg breaks. While this is very easy to understand, it is inefficient.
For a building with 100 steps –
- Drop the egg from step 1.
- If it doesn’t break, drop it from step 2.
- Continue this process until the egg breaks.
This method could take up to 100 trials in the worst case (if the egg only breaks on the 100th step).
.
- Binary Search Method
Binary search is a more efficient method. The idea is to split the search interval in half each time you drop an egg.
For a building with 100 steps –
- Drop the egg from step 50.
- If it breaks, check steps 1 to 49.
- If it doesn’t break, check steps 51 to 100.
- Repeat the process.
The binary search method will take at most log2(n) trials (about 7 trials for 100 steps), but it assumes you can use an infinite number of eggs, which is not practical for this problem. We have only 2 eggs.
.
- Incremental Increase (Optimized Linear Search)
Another approach involves incrementally increasing the number of steps you skip each time, reducing the number of drops needed.
For a building with 100 steps –
- Drop the first egg at steps 10, 20, 30, …, 100.
- If it breaks at step 40, use the second egg to check steps 31 to 39.
- The worst case is that you make about 10 drops with the first egg and up to 9 more with the second egg.
.
- Square Root Strategy
The square root strategy involves dropping the egg at steps that are square roots of the total number of steps (for example, steps 1, 4, 9, 16, etc., for a 100-step building). If an egg breaks at a certain step, the previous steps (since the last square root step) are tested linearly to find the exact step where the egg can be dropped without breaking.
For a building with 100 steps –
- Drop the first egg at steps 1, 4, 9, 16, 25, …, 100.
- If it breaks at step 81, use the second egg to check steps 65 to 80.
- The worst case is that you make 100 step drops and egg broke. You have to drop the second egg from 82 to 99.
Linear Search: 100 trials
Binary Search: log2(100) ≈ 7 trials (assuming infinite eggs)
Incremental Increase: √100 + √100 ≈ 20 trials
Square Root Strategy: √100 + 18 = 28 trials
.
Dynamic Programming
To solve this problem using dynamic programming, we define a 2D table dp where dp[i][j] represents the minimum number of trials needed with i eggs and j steps.
- With 1 Egg – If you have only one egg, you have to try each floor from 1 to j because you cannot afford to break the egg prematurely. Thus, dp[1][j] = j.
- With 0 steps – If there are no steps, you need 0 trials, so dp[i][0] = 0 for any i.
- With 1 step – If there is only one step, you need exactly one trial, so dp[i][1] = 1 for any i.
To fill the dp table, use the following recurrence relation
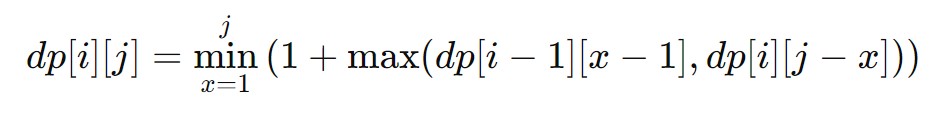
- dp[i-1][x-1] – Represents the scenario where the egg breaks at step x.
- dp[i][j-x] – Represents the scenario where the egg does not break at step x.
- 1 + … – The 1 account for the current drop.
.
Source Code for Eggs Dropping Problem
// COMPUTER GEEK – compgeek.co.in
// Write a program for Eggs Dropping Problem by Dynamic Programming
#include <stdio.h>
#include <stdlib.h>
// Function to compute the minimum number of trials needed with ‘eggs’ eggs and ‘steps’ steps (floors)
int eggDrop(int eggs, int steps) {
// Create a 2D DP table
int dp[eggs + 1][steps + 1];
// Base cases
for (int i = 1; i <= eggs; i++) {
dp[i][0] = 0; // 0 steps require 0 trials
dp[i][1] = 1; // 1 step requires 1 trial
}
for (int j = 1; j <= steps; j++) {
dp[1][j] = j; // 1 egg requires j trials for j steps (worst case)
}
// Fill the DP table
for (int i = 2; i <= eggs; i++) {
for (int j = 2; j <= steps; j++) {
dp[i][j] = 2147483647; // Initialize with a large value
for (int x = 1; x <= j; x++) {
int res = 1 + (dp[i – 1][x – 1] > dp[i][j – x] ? dp[i – 1][x – 1] : dp[i][j – x]);
if (res < dp[i][j]) {
dp[i][j] = res;
}
}
}
}
// Return the result for ‘eggs’ eggs and ‘steps’ steps
return dp[eggs][steps];
}
int main() {
int eggs, steps;
// Take inputs from the user
printf(“Enter the number of eggs: “);
scanf(“%d”, &eggs);
printf(“Enter the number of steps: “);
scanf(“%d”, &steps);
// Check for valid input
if (eggs <= 0 || steps <= 0) {
printf(“The number of eggs and steps must be positive integers.\n”);
return 1;
}
// Compute and print the minimum number of trials
int result = eggDrop(eggs, steps);
printf(“Minimum number of trials needed with %d eggs and %d steps is %d\n”, eggs, steps, result);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Eggs Dropping Problem by Dynamic Programming
#include <iostream>
#include <vector>
#include <algorithm> // for std::min
using namespace std;
// Function to compute the minimum number of trials needed with ‘eggs’ eggs and ‘steps’ steps (floors)
int eggDrop(int eggs, int steps) {
vector<vector<int>> dp(eggs + 1, vector<int>(steps + 1, 0));
// Base cases
for (int i = 1; i <= eggs; i++) {
dp[i][0] = 0; // 0 steps require 0 trials
dp[i][1] = 1; // 1 step requires 1 trial
}
for (int j = 1; j <= steps; j++) {
dp[1][j] = j; // 1 egg requires j trials for j steps (worst case)
}
// Fill the DP table
for (int i = 2; i <= eggs; i++) {
for (int j = 2; j <= steps; j++) {
dp[i][j] = INT_MAX; // Initialize with a large value
for (int x = 1; x <= j; x++) {
int res = 1 + max(dp[i – 1][x – 1], dp[i][j – x]);
dp[i][j] = min(dp[i][j], res);
}
}
}
// Return the result for ‘eggs’ eggs and ‘steps’ steps
return dp[eggs][steps];
}
int main() {
int eggs, steps;
// Take inputs from the user
cout << “Enter the number of eggs: “;
cin >> eggs;
cout << “Enter the number of steps: “;
cin >> steps;
// Check for valid input
if (eggs <= 0 || steps <= 0) {
cout << “The number of eggs and steps must be positive integers.” << endl;
return 1;
}
// Compute and print the minimum number of trials
int result = eggDrop(eggs, steps);
cout << “Minimum number of trials needed with ” << eggs << ” eggs and ” << steps << ” steps is ” << result << endl;
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Eggs Dropping Problem by Dynamic Programming
import java.util.Scanner;
public class EggDrop {
// Function to compute the minimum number of trials needed with ‘eggs’ eggs and ‘steps’ steps (floors)
public static int eggDrop(int eggs, int steps) {
int[][] dp = new int[eggs + 1][steps + 1];
// Base cases
for (int i = 1; i <= eggs; i++) {
dp[i][0] = 0; // 0 steps require 0 trials
dp[i][1] = 1; // 1 step requires 1 trial
}
for (int j = 1; j <= steps; j++) {
dp[1][j] = j; // 1 egg requires j trials for j steps (worst case)
}
// Fill the DP table
for (int i = 2; i <= eggs; i++) {
for (int j = 2; j <= steps; j++) {
dp[i][j] = Integer.MAX_VALUE; // Initialize with a large value
for (int x = 1; x <= j; x++) {
int res = 1 + Math.max(dp[i – 1][x – 1], dp[i][j – x]);
dp[i][j] = Math.min(dp[i][j], res);
}
}
}
// Return the result for ‘eggs’ eggs and ‘steps’ steps
return dp[eggs][steps];
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// Take inputs from the user
System.out.print(“Enter the number of eggs: “);
int eggs = scanner.nextInt();
System.out.print(“Enter the number of steps: “);
int steps = scanner.nextInt();
// Check for valid input
if (eggs <= 0 || steps <= 0) {
System.out.println(“The number of eggs and steps must be positive integers.”);
return;
}
// Compute and print the minimum number of trials
int result = eggDrop(eggs, steps);
System.out.println(“Minimum number of trials needed with ” + eggs + ” eggs and ” + steps + ” steps is ” + result);
scanner.close();
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for Eggs Dropping Problem by Dynamic Programming
def egg_drop(eggs, steps):
# Create a 2D DP table
dp = [[0] * (steps + 1) for _ in range(eggs + 1)]
# Base cases
for i in range(1, eggs + 1):
dp[i][0] = 0 # 0 steps require 0 trials
dp[i][1] = 1 # 1 step requires 1 trial
for j in range(1, steps + 1):
dp[1][j] = j # 1 egg requires j trials for j steps (worst case)
# Fill the DP table
for i in range(2, eggs + 1):
for j in range(2, steps + 1):
dp[i][j] = float(‘inf’) # Initialize with a large value
for x in range(1, j + 1):
res = 1 + max(dp[i – 1][x – 1], dp[i][j – x])
dp[i][j] = min(dp[i][j], res)
# Return the result for ‘eggs’ eggs and ‘steps’ steps
return dp[eggs][steps]
# Input from user
eggs = int(input(“Enter the number of eggs: “))
steps = int(input(“Enter the number of steps: “))
# Check for valid input
if eggs <= 0 or steps <= 0:
print(“The number of eggs and steps must be positive integers.”)
else:
# Compute and print the minimum number of trials
result = egg_drop(eggs, steps)
print(f”Minimum number of trials needed with {eggs} eggs and {steps} steps is {result}”)
Enter the number of eggs: 2
Enter the number of steps: 100
Minimum number of trials needed with 2 eggs and 100 steps is 14
=== Code Execution Successful ===
Alternative Method
In the context of the Egg Dropping Problem, k represents the number of trials you are allowed. To cover all n steps with k trials, the equation tells us how many steps can be tested with a given number of trials.
Consider the problem with n eggs and k steps –
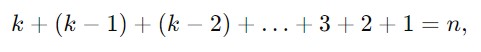
The left-hand side of the equation represents the sum of a series of decreasing numbers starting from k down to 1.
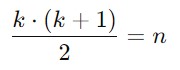
.
You can solve for k and this will give you the minimum number of trials needed.
For k = 100 steps and n = 2 eggs
The answer is k = 14. Means 14 trials is needed to check the highest step in which the egg broke up.
.
Time Complexity
The time complexity of this algorithm is O(k*n2), where k is the number of eggs and n is the number of floors. This is due to the nested loops for filling the DP table, where the inner loop iterates over all possible floors for each number of eggs and floors.
.
Space Complexity
The space complexity is O(k*n), because the algorithm uses a 2D table of size (k+1) x (n+1) to store the results of subproblems.
.
Advantages of Egg Dropping Problem
- The Egg Dropping Problem provides an efficient way to determine the minimum number of trials needed in a worst-case scenario, which is valuable in various real-world applications.
- It effectively demonstrates the application of dynamic programming, a fundamental algorithmic technique, for solving optimization problems by breaking them into simpler subproblems.
- The problem offers a predictive approach to understanding and minimizing the worst-case number of trials required, which is beneficial in scenarios where testing or experimentation is involved.
.
Disadvantages of Egg Dropping Problem
- Complexity for Large Inputs
- Although the algorithm itself is well-defined, implementing it efficiently can be complex and may require careful handling of edge cases and optimization considerations.
- Not Always Efficient
.
Applications of Egg Dropping Problem
- The problem’s principles can be applied to various optimization problems where resources are limited, and decisions need to be made to minimize risk or cost. Examples include network testing, system reliability assessments, and investment strategies.
- In game development, similar strategies can be used for decision-making processes where players need to balance resources and actions to achieve the best outcome with minimal attempts or risks.
- In software testing, especially for applications involving systems with limited resources, the egg dropping problem can be used to develop strategies for testing systems with minimal attempts, such as testing configurations or system limits.
Test Yourself
Q1- What is the main objective of the Egg Dropping Problem?
The main objective of the Egg Dropping Problem is to determine the minimum number of trials required to find the highest floor from which an egg can be dropped without breaking, using the fewest number of trials in the worst-case scenario. This is given a certain number of eggs and floors.
Q2- Explain why the linear search method is inefficient for large numbers of steps.
The linear search method is inefficient for large numbers of steps because it may require up to as many trials as there are steps in the worst-case scenario.
For example, with 100 steps, the worst-case scenario involves trying all 100 floors sequentially, resulting in a maximum of 100 trials.
Q3- Discuss the binary search method’s assumptions and limitations in the context of the Egg Dropping Problem.
The binary search method assumes that you have an unlimited number of eggs, which is not practical in the Egg Dropping Problem. It is efficient in terms of the number of trials (O(log n)), but it is not applicable when the number of eggs is limited because it does not account for scenarios where an egg might break.
Q4- How does the Incremental Increase method improve on the linear search method?
The Incremental Increase method improves upon the linear search method by skipping a progressively larger number of steps with each trial. This reduces the total number of trials needed compared to dropping from each step sequentially, balancing the risk of breaking an egg with the number of trials required.
Q5- What is the advantage of using the Square Root Strategy in the Egg Dropping Problem?
The Square Root Strategy reduces the number of trials by selecting steps that are square roots of the total number of steps.
It minimizes the worst-case number of trials compared to linear search and can be more efficient when you have a limited number of eggs, though it might not be as optimal as dynamic programming.
Q6- Explain the concept of dynamic programming in the context of the Egg Dropping Problem.
Dynamic programming solves the Egg Dropping Problem by breaking it down into smaller subproblems and storing the results of these subproblems in a table.
This approach avoids redundant calculations by reusing previously computed results to build up the solution for larger problems, leading to an efficient overall solution.
Q7- How does the recurrence relation used in the dynamic programming approach work?
The recurrence relation in dynamic programming for the Egg Dropping Problem calculates the minimum number of trials needed by considering all possible floors to drop an egg from.
It takes the maximum of the trials required if the egg breaks or does not break, adds one for the current trial, and finds the minimum of these values across all possible floors.
Q8- Which of the following is NOT an assumption of the Egg Dropping Problem?
Eggs are reusable
A broken egg should be removed
Every egg experiences a different reaction when it falls
If an egg does not break from a floor, it will not break from any higher floor
Ans – (3)
Explanation – All eggs experience the same reaction when they fall, which is one of the problem’s assumptions.
Q9- What is the best strategy if you have an unlimited number of eggs?
Linear Search
Incremental Increase
Square Root Strategy
Binary Search
Ans – (4)
Explanation – With an unlimited number of eggs, Binary Search is the best strategy as it requires the fewest trials by halving the search space each time.






