Dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems and solving each of these subproblems just once, storing their solutions.
The idea is that once one of these subproblems is solved, the solution is stored, so if the same subproblem is encountered again, the answer can be looked up rather than recomputed.
This approach can significantly reduce the time complexity of algorithms that solve problems with overlapping subproblems.
.
Recursion, divide and conquer, and dynamic programming are three algorithmic strategies that can often be confused because they all involve breaking problems down into smaller pieces. However, each has distinct characteristics and uses cases.
.
Recursion
- Recursion is a technique where a function calls itself as a subroutine, allowing the function to operate on simpler or smaller pieces of the problem until it reaches a base case, which is directly solvable without further recursion.
- This method often leads to simple solutions that are easy to understand.
- However, it can be inefficient due to repeated calculations.
- A common example of recursion is in computing Fibonacci numbers, where each number is the sum of the two preceding ones, defined as F(n) = F(n-1) + F(n-2).
.
Divide and Conquer
- Divide and Conquer is an algorithm design paradigm based on multi-branched recursion.
- In this approach, a problem is divided into two or more subproblems that are similar to the original problem but smaller in size.
- Each of these subproblems is solved recursively, and their solutions are then combined to solve the original problem.
- This method ensures that each subproblem is solved independently, and solutions to subproblems are combined to create a solution to the original problem.
- An example of divide and conquer is Merge Sort, which divides the array into halves, recursively sorts each half, and then merges the sorted halves back together.
.
Dynamic Programming
- Dynamic Programming is used when a problem has overlapping subproblems. Instead of solving each subproblem from scratch, dynamic programming seeks to solve each subproblem only once, store its solution in a table (usually an array), and reuse the solution by looking it up when needed.
- This approach applies when the problem has overlapping subproblems and an optimal substructure.
- Solutions of subproblems are stored for future use and the approach can follow either a top-down (with memoization) or bottom-up method.
- An illustrative example is calculating Fibonacci numbers using a bottom-up approach, where previous results are stored and used to calculate subsequent ones without redundant computations.
.
History
In 1950, Richard Bellman (Who contributed in the Bellman Ford Algorithm) introduced the term “dynamic programming” in a RAND memorandum titled “Dynamic Programming and the Principle of Optimality.“
Bellman chose the term “dynamic programming” to avoid controversy and bureaucratic resistance, as “programming” was often associated with tabulating and planning military activities. The term “dynamic” emphasized the sequential or time-varying nature of the problems being addressed.
Despite its name, dynamic programming has nothing to do with programming in the sense of writing code; rather, it refers to a method of solving problems by breaking them down into simpler subproblems and solving each subproblem just once, storing their solutions.
.
How Dynamic Programming Works
Dynamic programming can be implemented using two main techniques
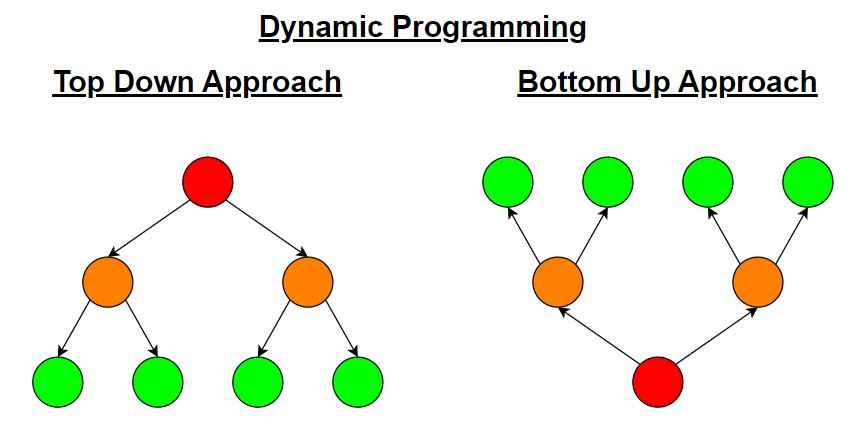
- Top-Down Approach (Memoization) – This approach involves writing the recursive algorithm and then storing the results of the subproblems in a table (generally using a hash table or an array). Each time a subproblem is solved, the result is stored in this table, and subsequent requests for the solution check the table before computing the solution.
- Bottom-Up Approach (Tabulation) – In this approach, the problem is solved by first looking at the smallest possible subproblems, solving those, and using their solutions to build up solutions to larger subproblems. This often involves filling up an n-dimensional table based on the recurrence relation that defines the problem.
Examples of Dynamic Programming
All Pair Shortest Path Problems – Algorithms like Floyd-Warshall use dynamic programming to find the shortest paths between all pairs of nodes in a weighted graph.
Knapsack Problem – Solving for the optimal set of items to include in a knapsack of limited capacity to maximize the total value, considering each combination of items.
Matrix Chain Multiplication – Determining the most efficient way to multiply a chain of matrices by finding the order of multiplications that minimizes the total number of scalar multiplications.
Longest Common Subsequence – LCS problem is a classic computer science problem that finds the longest subsequence common to all sequences in a set of sequences (often just two sequences). A subsequence is a sequence derived from another sequence by deleting some or no elements without changing the order of the remaining elements.
Coin Change Problem – Finding the number of ways to make change for a particular amount with a given set of coins.
Fibonacci Numbers – Calculating the nth Fibonacci number using dynamic programming to store previous results and avoid redundant calculations.
.
Advantages of Dynamic Programming
Optimality – Ensures an optimal solution is found if one exists.
Efficiency – Reduces time complexity by solving each subproblem once and storing the result.
Simplicity – Simplifies complex problems by breaking them into simpler subproblems.
Disadvantages of Dynamic Programming
Memory Consumption – Uses a lot of memory to store the results of subproblems.
Optimal Substructure and Overlapping Subproblems Required – Only effective when the problem have these properties; not all problems do.
Initialization Complexity – Setting up the correct states and transitions can be complex and error-prone.
.
Applications of Dynamic Programming
Computer Science – Used in algorithm design for problems like text editing distance, optimal search trees, and data compression.
Economics – Helps in solving resource allocation problems to maximize profit or minimize cost.
Operations Research – Useful in various optimization problems like the Knapsack problem, job scheduling issues, and in inventory management.
Bioinformatics – Employed in gene sequencing and alignment algorithms to find optimal alignments over time.
Robotics – Utilized in path planning algorithms to find the most efficient route for movement in an environment with obstacles.
Test Yourself
Q1- Why is dynamic programming often associated with the term “programming,” despite having nothing to do with coding?
Dynamic programming was named by Richard Bellman to avoid bureaucratic resistance associated with military planning, as “programming” was often associated with tabulating and planning military activities.
The term “dynamic” emphasized the sequential or time-varying nature of the problems being addressed.
Q2- Explain how dynamic programming can be both memory-intensive and memory-efficient at the same time.
Dynamic programming uses memory to store solutions to subproblems, making it memory-intensive.
However, by storing these solutions, it avoids redundant calculations, making it memory-efficient in terms of time complexity.
Q3- Can dynamic programming be applied to problems without overlapping subproblems? Justify your answer.
No, dynamic programming is only effective when a problem has overlapping subproblems and an optimal substructure. Without these properties, there’s no benefit to storing solutions to subproblems, as they won’t be reused.
Q4- Why is it important for a problem to have an optimal substructure for dynamic programming to be applicable?
An optimal substructure ensures that the optimal solution to the overall problem can be constructed from optimal solutions to its subproblems. This property is necessary for dynamic programming to work efficiently by recursively solving and storing solutions to subproblems.
Q5- What is meant by ‘overlapping subproblems’ in dynamic programming?
Overlapping subproblems refer to a scenario where the same smaller problems are solved multiple times in the process of solving the larger problem.
Dynamic programming is used to optimize such situations by storing the solutions to these subproblems the first time they are solved, thereby avoiding the need for re-computation.
Q6- Describe the process of tabulation in dynamic programming.
Tabulation is the strategy of solving dynamic programming problems by filling up a table (usually a 2D array) in a bottom-up manner. It starts by solving the smallest subproblems and uses their solutions to build up solutions to progressively larger subproblems.
Q7- What challenges might one face when implementing dynamic programming solutions?
The main challenges include determining the states and the transition between states, dealing with the initialization of the DP table, and managing the space and time complexity, which can become substantial with larger input sizes.
Q8- Difference between Greedy Algorithm and Dynamic Programming?
| Aspect | Greedy Algorithm | Dynamic Programming |
|---|---|---|
| Basic Concept | Builds a solution piece by piece, always choosing the next piece that offers the most immediate benefit. | Breaks down problems into smaller sub-problems, solves each sub-problem just once, and stores their solutions for future use. |
| Approach | Makes a locally optimal choice at each step, hoping that this choice will lead to a globally optimal solution. | Considers all possible solutions by solving subproblems recursively and using past knowledge to inform future decisions. |
| Problem Solving | Does not look backward or revise previous choices. | May revisit and revise decisions based on new information from solving subproblems. |
| Efficiency | Often more efficient in terms of execution time since it makes only one pass over the data. | Less efficient in terms of execution time due to the overhead of recursion and maintaining table entries, but often more efficient in terms of achieving the optimal solution. |
| Optimality | Does not always produce an optimal solution, but when it does, the algorithm is typically simpler and faster. | Always produces an optimal solution provided the problem exhibits optimal substructure and overlapping subproblems. |
| Usage | Used when a problem guarantees that local optimization leads to global solution, or if a good approximation is acceptable. | Used when the problem can be broken down into similar smaller problems and solutions need to be reused. |
| Memory Usage | Generally uses less memory as it does not store past results. | Uses more memory to store the results of subproblems in tables. |
| Examples | Fractional Knapsack problem, Prim’s and Kruskal’s algorithms for Minimum Spanning Tree. | Fibonacci numbers, Knapsack problem, Shortest paths (e.g., Bellman-Ford), Matrix chain multiplication. |
Q9- Which of the following problems can be solved using dynamic programming?
Finding the maximum number in an array
Binary search
Calculating the nth Fibonacci number
Determining if a graph is bipartite
Ans – (3)
Explanation – The Fibonacci sequence is a classic example of a problem that exhibits both optimal substructure and overlapping subproblems, making it suitable for dynamic programming.
Q10- Which approach does not typically use recursion?
Divide and conquer
Dynamic programming using memoization
Dynamic programming using tabulation
Depth-first search
Ans – (3)
Explanation – Tabulation is a bottom-up approach that typically uses iterative solutions instead of recursion to fill out a table of solutions.
Q11- What does memoization typically use to store results?
Stack
Queue
Hash table
Priority queue
Ans – (3)
Explanation – Memoization often uses a hash table (or a similar data structure) to store the results of subproblems for quick lookup.
Q12- In the context of dynamic programming, what is ‘state’?
A condition triggered by an event
A representation of a subproblem
A type of data structure
A debugging breakpoint
Ans – (2)
Explanation – In dynamic programming, a ‘state‘ typically refers to a specific configuration that represents a subproblem whose solution is needed to build up to larger solutions.
Q13- Which problem is a classic example of not having overlapping subproblems?
Longest Common Subsequence
Merge Sort
Coin Change
All Pair Shortest Path
Ans – (2)
Explanation – Merge Sort does not have overlapping subproblems because each subproblem is independent and does not recur in the solution of other subproblems.
Q14- Which algorithm uses dynamic programming to find the shortest paths between all pairs of nodes in a weighted graph?
Dijkstra’s Algorithm
Bellman-Ford Algorithm
Floyd-Warshall Algorithm
Kruskal’s Algorithm
Ans – (3)
Explanation – Floyd-Warshall Algorithm






