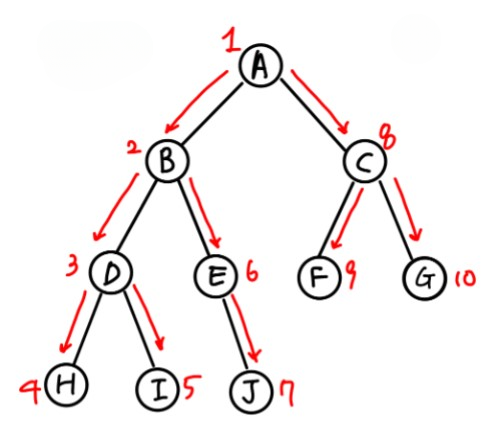
Introduction to Depth First Search Algorithm
.
Depth First Search (DFS) is a fundamental algorithm used in the field of computer science, specifically in the design and analysis of algorithms.
It is primarily employed for traversing or searching tree or graph data structures.
DFS explores as far as possible along each branch before backtracking, making it particularly useful for solving problems involving interconnected nodes.
.
History
DFS originated from maze-solving techniques by Charles Pierre Trémaux in the 19th century. Formalized by Charles Leonard Hamblin in 1954, it recursively explores graph/tree structures.
DFS gained prominence in the 1960s, becoming fundamental in graph theory and various applications like network analysis and AI.
Trémaux and Hamblin’s contributions paved the way for DFS as a crucial algorithm in computer science.
They proposed a method for solving mazes by consistently following either the left-hand or right-hand rule.
By adhering to this rule, where you always turn in the same direction (left or right) at every junction, it becomes possible to navigate through the maze and eventually reach the exit. This approach simplifies the maze-solving process and provides a systematic way to explore and solve maze puzzles.
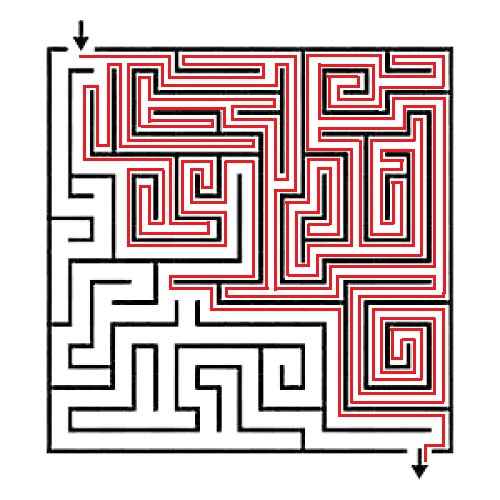
It follows the left-hand rule and with this method we come out from exit.
In solving this maze, we follow left hand rule of Depth First Search (DFS) Algorithm, but here it is not the complete DFS. I tell you why
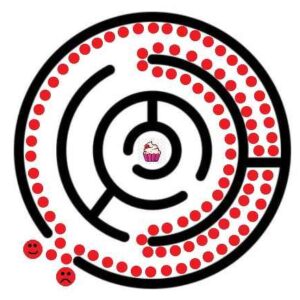
In this maze, we follow the left-hand rule and we could not even reach the cupcake in the innermost circle. That’s why it’s not DFS because DFS will cover all the remaining points in the graph, including the cupcake.
.
Definition
- Basic Principle – It starts at a selected node (often referred to as the “root“) and explores as far as possible along each branch

- Depth First Search (DFS) can be likened to a preorder traversal of a tree. In a preorder traversal, the algorithm starts from the root node and visits each node’s subtree recursively in a depth-first manner. Similarly, in DFS, the algorithm explores as far as possible along each branch before backtracking, effectively traversing the entire graph or tree structure in a depth-first manner.
.
- DFS keeps track of previously visited nodes using timestamps to prevent infinite loops or non-termination. If the search is conducted without keeping track of previously visited nodes, it will visit the nodes in the following order: A, B, E, F, H D, A, B, E, F, H, etc. This will keep the user stuck in the A, B, E, F, H, D cycle and prevent them from ever reaching C and G.
- Each vertex has two timestamps – 1. Discovery Timestamp d[v] 2. Finishing Timestamp f[v], and for every vertex, its discovery timestamp < finishing timestamp.
- Recursive Nature – DFS employs recursion or a stack-based approach to traverse the graph, visiting adjacent unvisited nodes until all nodes are visited or a specific condition is met.
.
Algorithm of DFS
- Initialization:
- Create a stack to store vertices.
- Initialize all vertices as undiscovered (white).
- DFS Algorithm:
- Start from a chosen vertex and mark it as discovered (gray).
- Push the vertex onto the stack.
- While the stack is not empty
- Peek at the top vertex of the stack.
- If the vertex has undiscovered neighbors
- Choose an undiscovered neighbor.
- Mark the neighbor as discovered (gray) and push it onto the stack.
- If the vertex has no undiscovered neighbors or all neighbors are visited
- Pop the vertex from the stack.
- Mark the vertex as finished (black).
- Repeat until all vertices are visited.
- Recording Discovery and Finishing Times
- Initialize a global timestamp variable.
- When a vertex is discovered, record its discovery time as the current timestamp.
- When a vertex is finished, record its finishing time as the current timestamp.
- Increment the timestamp after each discovery or finishing event.
- Backtracking
- After DFS traversal completes, if needed for specific applications, backtrack through the graph to find paths or perform additional operations.
.
Example
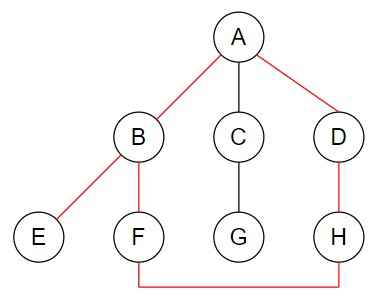
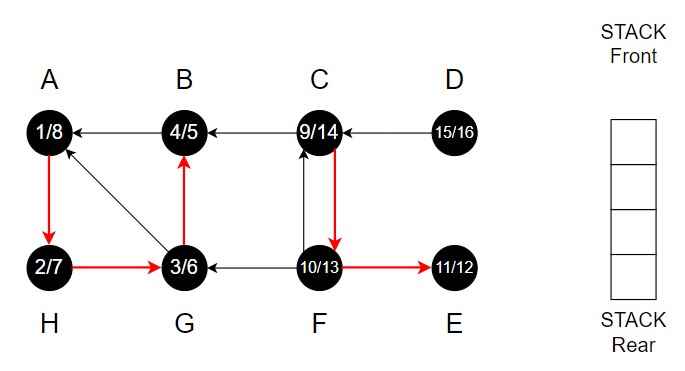
Step 1 – Start from vertex A.
Color of A = Grey
Discover time = 1
Vertex A is top of the Stack.
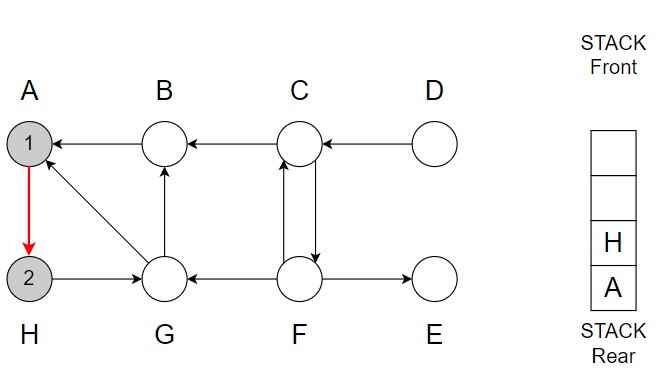
Step 2 – A -> H
Color of H = Grey
Discover time = 2
Vertex H is top of the Stack.
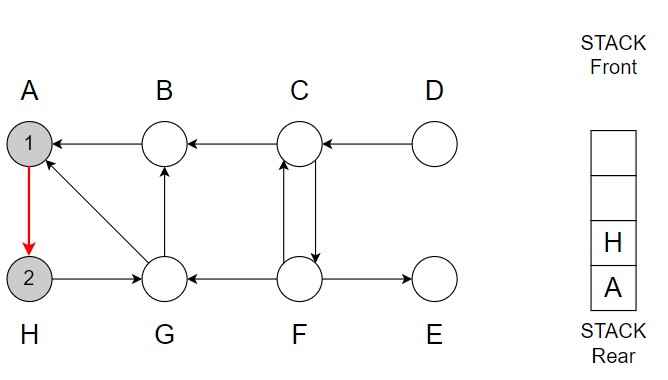
Step 3 – H -> G
Color of G = Grey
Discover time = 3
Vertex G is top of the Stack.
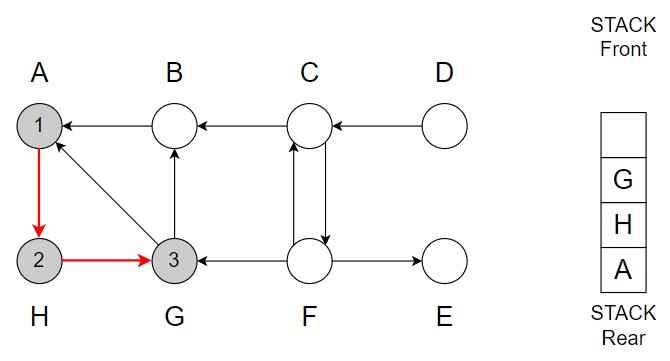
Step 4 – G -> B
Color of B = Grey
Discover time = 4
Vertex B is top of the Stack.
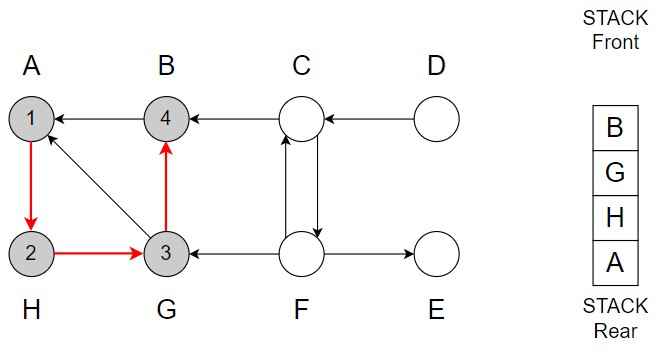
Step 5 – B -> only A (A is already in the Stack)
Pop B from the Stack
Color of B = Black
Finishing time = 5 and backtrack.
Vertex G is top of the Stack.
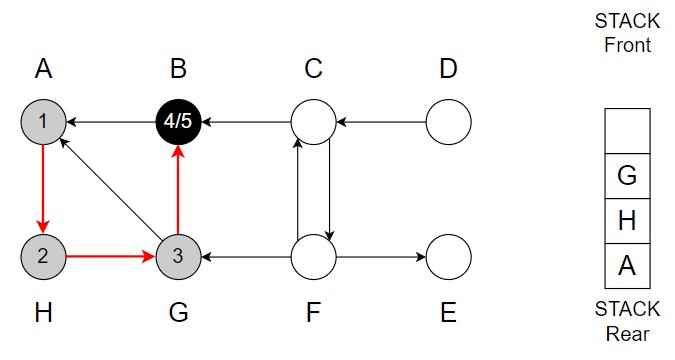
Step 6 – B <- G (G -> A and A is already in the Stack)
Pop G from the Stack
Color of G = Black
Finishing time = 6 and backtrack.
Vertex H is top of the Stack.
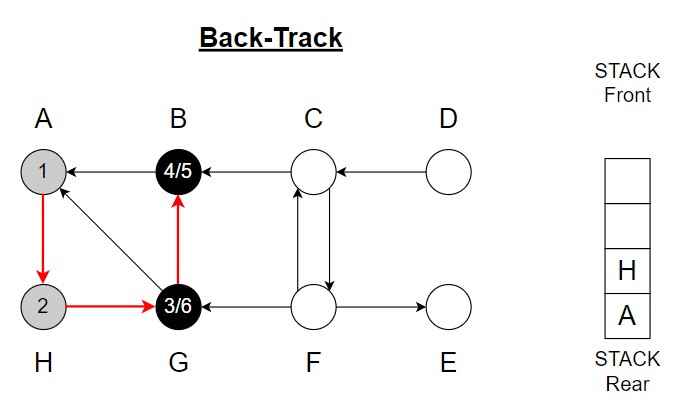
Step 7 – G <- H
Pop H from the Stack
Color of H = Black
Finishing time = 7 and backtrack.
Vertex A is top of the Stack.
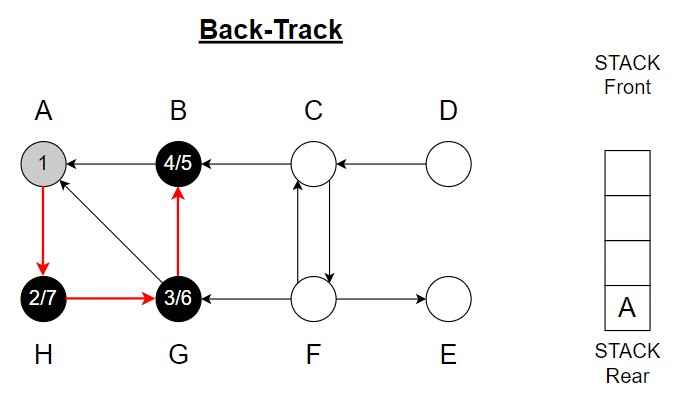
Step 8 – H -> A
Pop A from the Stack
Color of A = Black
Finishing time = 8.
Stack is empty.
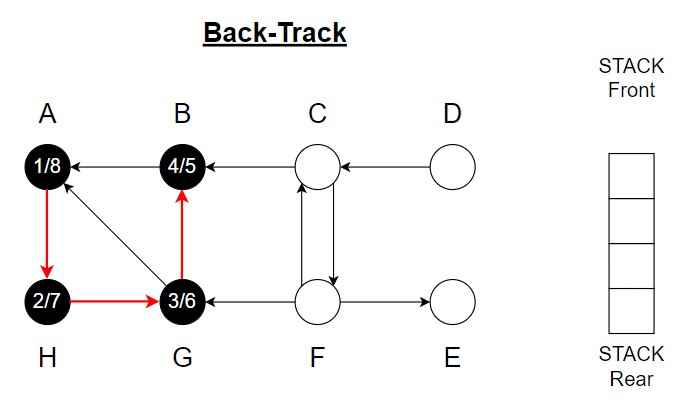
Step 9 – Choose vertex C.
Color of C = Grey
Discover time = 9
Vertex C is top of the Stack.
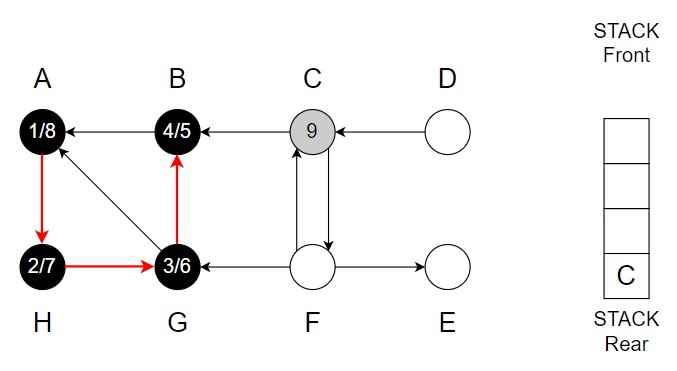
Step 10 – C -> F
Color of F = Grey
Discover time = 10
Vertex F is top of the Stack.
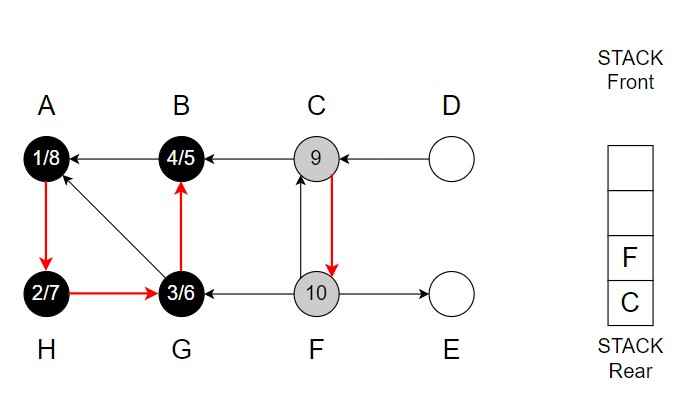
Step 11 – F -> E
Color of E = Grey
Discover time = 11
Vertex E is top of the Stack.
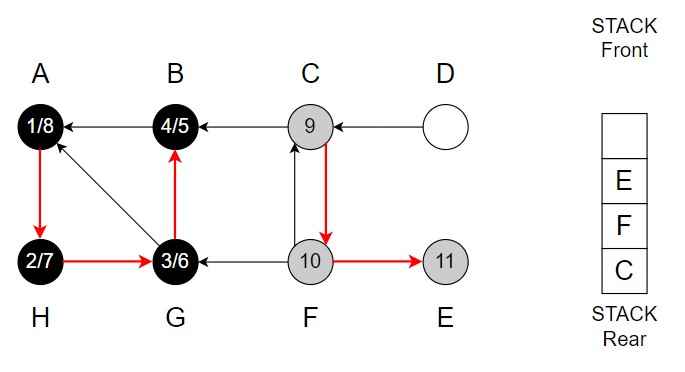
Step 12 – E has no adjacent vertex.
Pop E from the Stack.
Color of E = Black
Finishing time = 12 and backtrack.
Vertex F is top of the Stack.
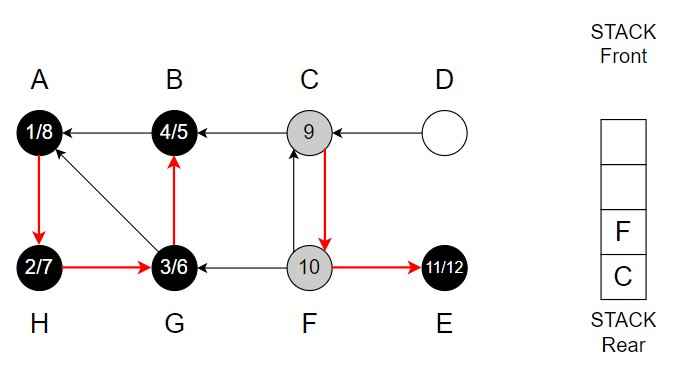
Step 13 – E <- F
Pop F from the Stack.
Color of F = Black
Finishing time = 13
Vertex C is top of the Stack.
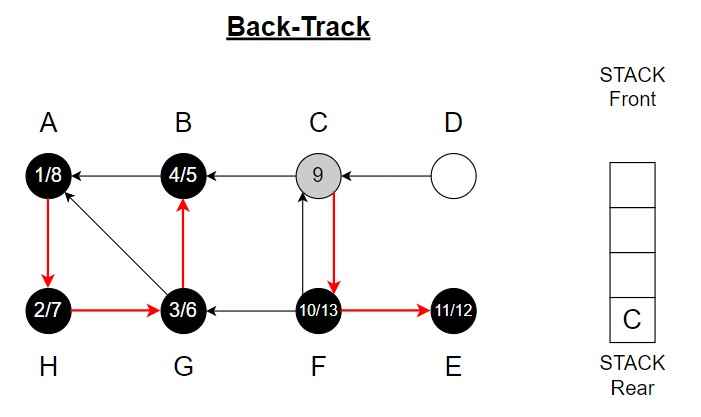
Step 14 – F <- C
Pop C from the Stack.
Color of C = Black
Finishing time = 14
Stack is empty.
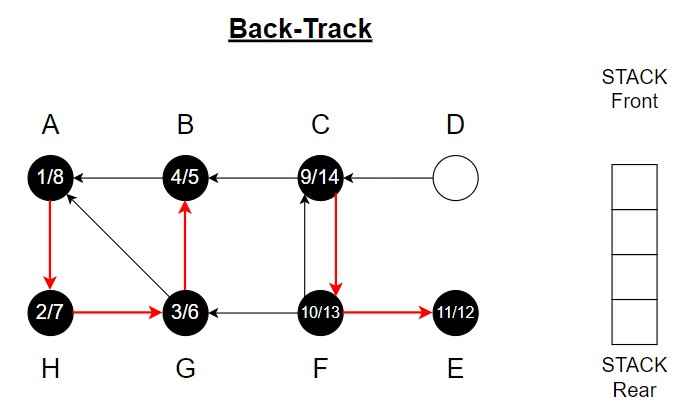
Step 15 – Choose vertex D.
Color of D = Grey
Discover time = 15
Vertex D is top of the Stack.
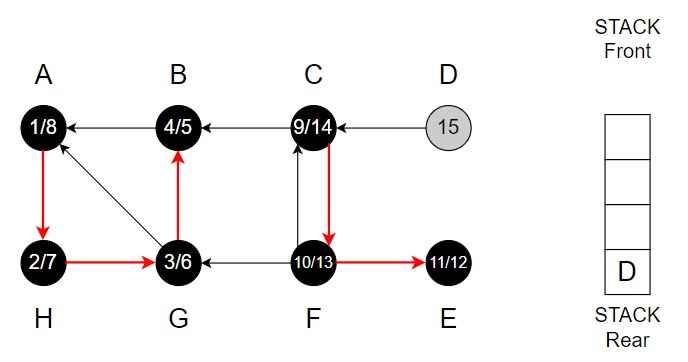
Step 16 – D has adjacent vertex C and C is already black.
Pop D from the Stack.
Color of D = Black
Finishing time = 16
Stack is empty.
.
Source Code of Depth First Search
#include <stdio.h>
#include <stdlib.h>
#define WHITE 0
#define GRAY 1
#define BLACK 2
#define MAX_VERTICES 100
// Structure to represent a node in the adjacency list
struct Node {
int vertex;
struct Node* next;
};
// Structure to represent the graph
struct Graph {
struct Node* adjacencyList[MAX_VERTICES];
int color[MAX_VERTICES];
int discoveryTime[MAX_VERTICES];
int finishingTime[MAX_VERTICES];
int timestamp;
int vertices;
};
// Function to initialize a graph
struct Graph* createGraph(int vertices) {
struct Graph* graph = (struct Graph*)malloc(sizeof(struct Graph));
graph->vertices = vertices;
graph->timestamp = 0;
for (int i = 0; i < vertices; ++i) {
graph->adjacencyList[i] = NULL;
graph->color[i] = WHITE;
}
return graph;
}
// Function to add an edge to the graph
void addEdge(struct Graph* graph, int src, int dest) {
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->vertex = dest;
newNode->next = graph->adjacencyList[src];
graph->adjacencyList[src] = newNode;
}
// Depth First Search algorithm
void DFS(struct Graph* graph, int vertex) {
graph->color[vertex] = GRAY;
graph->discoveryTime[vertex] = ++(graph->timestamp);
printf(“Visited vertex %d\n”, vertex);
struct Node* temp = graph->adjacencyList[vertex];
while (temp != NULL) {
int neighbor = temp->vertex;
if (graph->color[neighbor] == WHITE) {
DFS(graph, neighbor);
}
temp = temp->next;
}
graph->color[vertex] = BLACK;
graph->finishingTime[vertex] = ++(graph->timestamp);
}
int main() {
int vertices, edges;
printf(“Enter the number of vertices: “);
scanf(“%d”, &vertices);
struct Graph* graph = createGraph(vertices);
printf(“Enter the number of edges: “);
scanf(“%d”, &edges);
printf(“Enter the edges (src dest):\n”);
for (int i = 0; i < edges; ++i) {
int src, dest;
scanf(“%d %d”, &src, &dest);
addEdge(graph, src, dest);
}
printf(“Depth First Search Traversal:\n”);
for (int i = 0; i < vertices; ++i) {
if (graph->color[i] == WHITE) {
DFS(graph, i);
}
}
printf(“Discovery and Finishing Times:\n”);
for (int i = 0; i < vertices; ++i) {
printf(“Vertex %d: Discovery Time – %d, Finishing Time – %d\n”, i, graph->discoveryTime[i], graph->finishingTime[i]);
}
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Depth First Search
#include <iostream>
#include <vector>
using namespace std;
#define WHITE 0
#define GRAY 1
#define BLACK 2
#define MAX_VERTICES 100
struct Node {
int vertex;
Node* next;
};
struct Graph {
Node* adjacencyList[MAX_VERTICES];
int color[MAX_VERTICES];
int discoveryTime[MAX_VERTICES];
int finishingTime[MAX_VERTICES];
int timestamp;
int vertices;
Graph(int V) {
vertices = V;
timestamp = 0;
for (int i = 0; i < V; ++i) {
adjacencyList[i] = nullptr;
color[i] = WHITE;
}
}
void addEdge(int src, int dest) {
Node* newNode = new Node;
newNode->vertex = dest;
newNode->next = adjacencyList[src];
adjacencyList[src] = newNode;
}
void DFS(int vertex) {
color[vertex] = GRAY;
discoveryTime[vertex] = ++timestamp;
cout << “Visited vertex ” << vertex << endl;
Node* temp = adjacencyList[vertex];
while (temp != nullptr) {
int neighbor = temp->vertex;
if (color[neighbor] == WHITE) {
DFS(neighbor);
}
temp = temp->next;
}
color[vertex] = BLACK;
finishingTime[vertex] = ++timestamp;
}
};
int main() {
int vertices, edges;
cout << “Enter the number of vertices: “;
cin >> vertices;
Graph graph(vertices);
cout << “Enter the number of edges: “;
cin >> edges;
cout << “Enter the edges (src dest):” << endl;
for (int i = 0; i < edges; ++i) {
int src, dest;
cin >> src >> dest;
graph.addEdge(src, dest);
}
cout << “Depth First Search Traversal:” << endl;
for (int i = 0; i < vertices; ++i) {
if (graph.color[i] == WHITE) {
graph.DFS(i);
}
}
cout << “Discovery and Finishing Times:” << endl;
for (int i = 0; i < vertices; ++i) {
cout << “Vertex ” << i << “: Discovery Time – ” << graph.discoveryTime[i] << “, Finishing Time – ” << graph.finishingTime[i] << endl;
}
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Depth First Search
import java.util.*;
class Node {
int vertex;
Node next;
public Node(int vertex) {
this.vertex = vertex;
this.next = null;
}
}
class Graph {
Node[] adjacencyList;
int[] color;
int[] discoveryTime;
int[] finishingTime;
int timestamp;
int vertices;
public Graph(int V) {
vertices = V;
adjacencyList = new Node[V];
color = new int[V];
discoveryTime = new int[V];
finishingTime = new int[V];
timestamp = 0;
for (int i = 0; i < V; ++i) {
adjacencyList[i] = null;
color[i] = 0;
}
}
public void addEdge(int src, int dest) {
Node newNode = new Node(dest);
newNode.next = adjacencyList[src];
adjacencyList[src] = newNode;
}
public void DFS(int vertex) {
color[vertex] = 1;
discoveryTime[vertex] = ++timestamp;
System.out.println(“Visited vertex ” + vertex);
Node temp = adjacencyList[vertex];
while (temp != null) {
int neighbor = temp.vertex;
if (color[neighbor] == 0) {
DFS(neighbor);
}
temp = temp.next;
}
color[vertex] = 2;
finishingTime[vertex] = ++timestamp;
}
}
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print(“Enter the number of vertices: “);
int vertices = scanner.nextInt();
Graph graph = new Graph(vertices);
System.out.print(“Enter the number of edges: “);
int edges = scanner.nextInt();
System.out.println(“Enter the edges (src dest):”);
for (int i = 0; i < edges; ++i) {
int src = scanner.nextInt();
int dest = scanner.nextInt();
graph.addEdge(src, dest);
}
System.out.println(“Depth First Search Traversal:”);
for (int i = 0; i < vertices; ++i) {
if (graph.color[i] == 0) {
graph.DFS(i);
}
}
System.out.println(“Discovery and Finishing Times:”);
for (int i = 0; i < vertices; ++i) {
System.out.println(“Vertex ” + i + “: Discovery Time – ” + graph.discoveryTime[i] + “, Finishing Time – ” + graph.finishingTime[i]);
}
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for Depth First Search
WHITE = 0
GRAY = 1
BLACK = 2
class Node:
def __init__(self, vertex):
self.vertex = vertex
self.next = None
class Graph:
def __init__(self, V):
self.vertices = V
self.adjacencyList = [None] * V
self.color = [WHITE] * V
self.discoveryTime = [0] * V
self.finishingTime = [0] * V
self.timestamp = 0
def addEdge(self, src, dest):
newNode = Node(dest)
newNode.next = self.adjacencyList[src]
self.adjacencyList[src] = newNode
def DFS(self, vertex):
self.color[vertex] = GRAY
self.discoveryTime[vertex] = self.timestamp + 1
print(“Visited vertex”, vertex)
temp = self.adjacencyList[vertex]
while temp:
neighbor = temp.vertex
if self.color[neighbor] == WHITE:
self.DFS(neighbor)
temp = temp.next
self.color[vertex] = BLACK
self.finishingTime[vertex] = self.timestamp + 1
self.timestamp += 1
def main():
vertices = int(input(“Enter the number of vertices: “))
graph = Graph(vertices)
edges = int(input(“Enter the number of edges: “))
print(“Enter the edges (src dest):”)
for _ in range(edges):
src, dest = map(int, input().split())
graph.addEdge(src, dest)
print(“Depth First Search Traversal:”)
for i in range(vertices):
if graph.color[i] == WHITE:
graph.DFS(i)
print(“Discovery and Finishing Times:”)
for i in range(vertices):
print(“Vertex”, i, “: Discovery Time -“, graph.discoveryTime[i], “, Finishing Time -“, graph.finishingTime[i])
if __name__ == “__main__”:
main()
Enter the number of vertices: 8
Enter the number of edges: 11
Enter the edges (src dest):
0 4
4 5
5 0
1 0
5 1
2 1
6 5
6 2
2 6
3 2
6 7
Depth First Search Traversal:
Visited vertex 0
Visited vertex 4
Visited vertex 5
Visited vertex 1
Visited vertex 2
Visited vertex 6
Visited vertex 7
Visited vertex 3
Discovery and Finishing Times:
Vertex 0: Discovery Time – 1, Finishing Time – 8
Vertex 1: Discovery Time – 4, Finishing Time – 5
Vertex 2: Discovery Time – 9, Finishing Time – 14
Vertex 3: Discovery Time – 15, Finishing Time – 16
Vertex 4: Discovery Time – 2, Finishing Time – 7
Vertex 5: Discovery Time – 3, Finishing Time – 6
Vertex 6: Discovery Time – 10, Finishing Time – 13
Vertex 7: Discovery Time – 11, Finishing Time – 12
=== Code Execution Successful ===
“White Path” Property
The “white path” property is a characteristic of Depth First Search (DFS) trees in graph traversal. When performing DFS on a graph, the DFS tree is formed as a result of the traversal process. The white path property refers to the structure of this DFS tree.
In a DFS tree, a “white path” is a path from the root of the tree to a leaf node (a node with no outgoing edges) such that all edges along the path are tree edges, and all nodes on the path are white (i.e., undiscovered) when the path is first traversed.
Here’s a breakdown of the white path property
- Root Node – The root of the DFS tree is the starting vertex of the DFS traversal.
- Path to Leaf Node – A white path extends from the root of the tree to a leaf node. Along this path, every node (except possibly the leaf node itself) is connected to its parent node by a tree edge.
- White Nodes – All nodes along the white path are white, indicating that they have not been discovered before the traversal reaches them.
- Tree Edges – Each edge along the white path is a tree edge, meaning it connects a node to its parent in the DFS tree.
The white path property is useful in understanding the structure of DFS trees and analyzing the behavior of DFS algorithms.
It helps to identify and characterize paths within the DFS tree and can be used in algorithm design and analysis.
Additionally, the white path property can aid in identifying certain properties or patterns in graphs being traversed using DFS.
.
Four main classifications for directed edges in DFS
Tree Edges –
Definition – Tree edges are edges that are part of the DFS tree being constructed during traversal.
Characteristics –
- Tree edges always point from a parent node to its child node in the DFS tree.
- They represent the discovery of a new vertex and the expansion of the DFS tree.
- Tree edges are crucial for constructing the DFS tree and maintaining the traversal order.
Back Edges –
Definition – Back edges are edges that connect a vertex to one of its ancestors in the DFS tree in a directed graph.
Characteristics –
- Back edges form cycles in the graph.
- They point from a descendant node back to one of its ancestor nodes in the DFS tree.
- Back edges indicate the presence of cycles in the graph and are important for cycle detection algorithms.
Forward Edges –
Definition – Forward edges are edges that connect a vertex to one of its descendants in the DFS tree in a directed graph.
Characteristics –
- Forward edges do not form cycles in the graph.
- They point from an ancestor node to one of its descendant nodes in the DFS tree.
- Forward edges can be used in various algorithms, such as topological sorting, where the ordering of vertices matters.
Cross Edges –
Definition – Cross edges are edges that do not fall into any of the above categories.
Characteristics –
- Cross edges do not form cycles with the DFS tree.
- They connect vertices that are neither ancestors nor descendants of each other in the DFS tree.
- Cross edges may not have specific applications in DFS-based algorithms but can be useful for analyzing graph properties.
.
Time Complexity
The time complexity of Depth First Search (DFS) depends on the representation of the graph and the specific implementation details. However, in general, the time complexity of DFS is O(V + E), where V is the number of vertices and E is the number of edges in the graph.
.
Space Complexity
The space complexity of Depth First Search (DFS) is primarily determined by the memory used to store the traversal stack and the auxiliary data structures required during the traversal process.
In the worst-case scenario, where the graph is a dense graph with many edges, the space complexity of DFS can be O(V), where V is the number of vertices in the graph.
However, in the average case and for sparse graphs, the space complexity of DFS is often lower, typically ranging from O(log V) to O(V) depending on the implementation and specific details of the graph structure.
.
Application
Graph Traversal – DFS visits every vertex and edge in a graph structure with efficiency.
Pathfinding – This technique helps in route planning and maze solving by assisting in the identification of pathways between two vertices in a graph.
Cycle Detection – DFS uses back edge identification to find cycles in either directed or undirected graphs.
Topological Sorting – In directed acyclic graphs (DAGs), DFS makes it easier for vertices to be arranged so that directed edges follow a predetermined sequence.
Connected Components – This shows groups of vertices where every vertex can be reached from every other vertex in the group.
Strongly Connected Components – In directed graphs, DFS finds subsets in which all vertices are reachable from other vertices through directed paths.
Network Analysis – DFS searches networks to find important nodes or pathways, discover patterns, and examine connectivity.
Test Yourself
Q1- Explain the concept of the “white path” property in Depth First Search (DFS) traversal and its significance in analyzing DFS trees
The white path property refers to a path from the root of a DFS tree to a leaf node, where all nodes along the path are undiscovered (white) when first traversed.
This property is essential in understanding the structure of DFS trees and helps in analyzing traversal patterns and characteristics. It signifies the progression of the DFS algorithm from the root to leaf nodes, maintaining the integrity of tree edges and aiding in identifying specific paths within the tree.
Q2- Discuss the significance of back edges in DFS traversal, particularly in the context of cycle detection in directed graphs.
Back edges are crucial in DFS traversal as they indicate the presence of cycles in a directed graph. These edges connect a vertex to one of its ancestors in the DFS tree, forming a cycle. In cycle detection algorithms, detecting back edges helps in identifying and breaking cycles, ensuring the graph remains acyclic. By recognizing back edges, DFS traversal can determine the existence of cycles and prevent infinite loops in algorithms that rely on graph traversal.
Q3- Compare and contrast the time and space complexity of DFS with other graph traversal algorithms like Breadth First Search (BFS).
DFS and BFS are both graph traversal algorithms, but they differ in their time and space complexity.
DFS has a time complexity of O(V + E) and a space complexity of O(V), where V is the number of vertices and E is the number of edges.
In contrast, BFS has a time complexity of O(V + E) and a space complexity of O(V + E), where the additional space is due to the queue used in BFS.
While DFS is more memory-efficient, BFS guarantees finding the shortest path in unweighted graphs.
Q4- Discuss the role of DFS in identifying strongly connected components (SCCs) in a directed graph and explain how Strongly Connected Components (SCCs) are different from connected components
DFS plays a crucial role in identifying strongly connected components (SCCs) in a directed graph by performing multiple DFS traversals.
SCCs are subsets of vertices where every vertex is reachable from every other vertex through directed paths. Unlike connected components, which apply to undirected graphs and indicate mutual connectivity, SCCs consider the direction of edges in directed graphs.
DFS identifies SCCs by traversing the graph and identifying nodes with back edges that form cycles, indicating the presence of strongly connected components.
Q5- Describe the initialization and termination conditions of the DFS algorithm, emphasizing the importance of marking vertices during traversal.
The initialization of DFS involves setting up data structures such as color arrays to track the traversal state of vertices.
During traversal, vertices are marked as discovered (gray) when first encountered and finished (black) when all adjacent vertices have been visited.
The termination condition occurs when all vertices have been visited, ensuring that every vertex is processed exactly once. Marking vertices prevents revisiting already explored paths, avoiding infinite loops and ensuring the completeness and correctness of the traversal process.
Q6- Explain the process of backtracking in DFS traversal and discuss its significance in pathfinding algorithms.
Backtracking in DFS traversal involves retracing steps and exploring alternative paths when no further progress can be made along the current path.
It is significant in pathfinding algorithms as it allows the algorithm to explore different routes to reach the destination.
By backtracking, DFS can backtrack to previously explored nodes, explore alternative paths, and ultimately find the optimal or desired path in maze-solving or routing problems.
Q7- Discuss the recursive nature of the DFS algorithm and explain how it facilitates graph traversal.
DFS employs recursion to traverse the graph by exploring adjacent unvisited nodes until all nodes are visited or a specific condition is met.
The recursive nature of DFS simplifies the traversal process, as it allows the algorithm to systematically explore each branch of the graph in a depth-first manner. By recursively visiting adjacent nodes, DFS efficiently explores the entire graph structure, uncovering paths and identifying connectivity patterns.
Q8- Illustrate the process of recording discovery and finishing times in DFS traversal and explain their significance in analyzing graph structures.
Discovery and finishing times are recorded during DFS traversal to timestamp the events of discovering and finishing exploring each vertex. These timestamps provide valuable information about the order in which vertices are discovered and finished, aiding in analyzing the structure and properties of the graph.
By comparing discovery and finishing times of vertices, one can infer relationships between vertices, identify cycles, and understand the overall topology of the graph.
Q9- Provide a real-world example where DFS can be applied to solve a practical problem, highlighting its relevance in various domains.
DFS can be applied to solve network analysis problems, such as finding the shortest path in a computer network or identifying critical nodes in a social network.
For example, in a computer network, DFS can be used to determine the most efficient route for data transmission between two nodes by exploring the network topology.
Similarly, in a social network, DFS can help identify influential individuals or communities by analyzing connections and interactions between users.
Q10- What is the time complexity of Depth First Search (DFS) algorithm?
O(V)
O(V + E)
O(E)
O(log V)
Ans – (2)
Explanation – DFS has a time complexity of O(V + E), where V is the number of vertices and E is the number of edges in the graph.
Q11- Which data structure is commonly used to implement the stack in Depth First Search (DFS)?
Queue
Array
Linked List
Stack
Ans – (4)
Explanation – DFS typically uses a stack data structure to keep track of vertices during traversal.
Q12- What is the primary purpose of marking vertices as “discovered” and “finished” in DFS traversal?
To prevent infinite loops
To identify strongly connected components
To record traversal timestamps
To maintain traversal order
Ans – (4)
Explanation – Marking vertices helps in maintaining the traversal order and avoiding revisiting already explored paths.
Q13- In DFS traversal, what is the significance of the “white path” property?
It ensures the completeness of traversal
It helps in identifying cycle-free paths
It indicates the existence of a spanning tree
It represents unexplored paths in the graph
Ans – (2)
Explanation – The white path property signifies paths from the root to leaf nodes where all nodes are undiscovered, indicating cycle-free paths.
Q14- Which phase of DFS traversal involves recording traversal timestamps for vertices?
Initialization
Discovery
Finishing
Backtracking
Ans – (3)
Explanation – The finishing phase of DFS traversal involves recording finishing timestamps for vertices.