Design & Analysis of Algorithm logo

DAA Unit 3 Part 2 MCQs

PREV
NEXT
Menu
Unit 3

Advance Data Structure:- Binary Search Tree, AVL Tree, Red-Black Tree, B-Tree, B+ Tree, Binomial Tree, Binomial Heap, Fibonacci Heap, Trie, Skip List.

Q21 – Which of the following statement(s) is/are correct about red-black binary tree?
I. Every node is either red or black.
II. Every leaf node is red.
III. When a node is red and both its children are black. (DSSSB PGT 2021)
  1. III and II
  2. I and III
  3. I and II
  4. I, II and III

Ans – (2)

Explanation – These four requirements must be met by a red-black tree:

The root node is always a black node.

It is believed that a nil is black.

Every red node has black children.

The equal number of black nodes appear on each path from the root to the leaf nodes.

https://compgeek.co.in/red-black-tree/ to know more.

Q22 – Consider a max heap, represented by the array:
23, 17, 14, 6, 13, 10, 1, 5
If a value 20 is inserted into this heap, then what will be the new max heap (DSSSB PGT 2021)
  1. 23, 17, 20, 14, 13, 10, 6, 5, 1
  2. 23, 20, 17, 14, 13, 10, 6, 5, 1
  3. 23, 20, 14, 17, 13, 10, 1, 5, 6
  4. 23, 17, 4, 6, 13, 10, 1, 5, 20

Ans – (3)

Explanation –

HEAP

So, Array is 23, 20, 14, 17 13, 10, 1, 5, 6

Q23 – The maximum height of a red black tree with n internal nodes is (DSSSB PGT 2018)
  1. log(n+1)
  2. 2logn
  3. 2log(n+1)
  4. 2+logn

Ans – (3)

Explanation –

The claim follows from the fact that in a binary tree, the longest root-to-leaf path has length k, and the number of nodes on this path is at least 2^k-1. Therefore, if we have n nodes in the tree, we must have n >= 2^k-1, which implies k <= log2(n+1).

For Red-Black trees, property states that every root-to-leaf path has the same number of black nodes. Therefore, if there is a path with at most k black nodes, then all paths have at most k black nodes. Hence, the longest root-to-leaf path in the tree has at most log2(n+1) black nodes.

Other property of Red-Black trees states that every red node has two black children. Therefore, in any path from the root to a leaf, the number of black nodes is at least half the number of nodes on the path (since every red node is followed by two black nodes). The root node is black. Therefore, the number of black nodes in the tree is at least half the number of nodes in the tree, which implies that the number of black nodes is at least ⌊ n/2 ⌋, and the height of Red-Black Tree is at most 2log(n+1).

Q24 – Which of the following can be defined as the number of sub-trees of a node? (DSSSB PGT 2018)
  1. Degree
  2. Forest
  3. Level
  4. Terminal nodes

Ans – (1)

Explanation –

The degree would be represented in a tree as the number of children it can have.

Q25 – A binary search tree where the subtrees of every node differ in height by at most 1 is called (DSSSB PGT 2018)
  1. Binary Search Tree
  2. B+ Tree
  3. AVL Tree
  4. Binary Tree

Ans – (3)

Explanation –

An AVL tree is called balanced when the difference of height is -1, 0, 1. It is also called balance factor (BF).

BALANCE FACTOR = Height of left subtree – Height of right subtree

That’s why |height(TL) – height(TR)| ≤ 1

https://compgeek.co.in/avl-tree/ to know more.

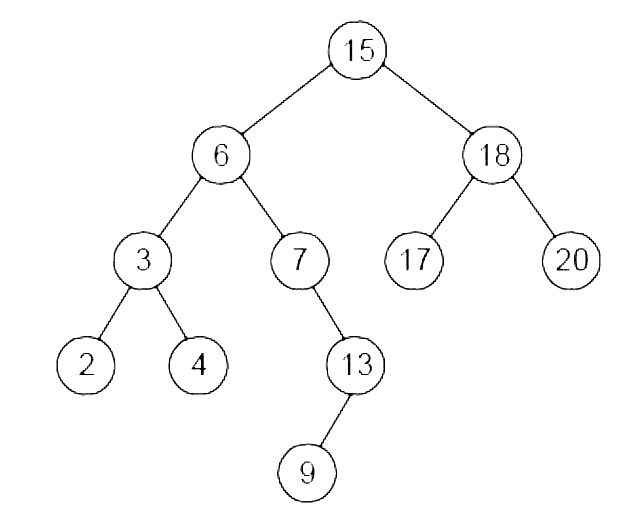
Q26 – What is the in-order successor of 15 in the given binary search tree? (ISRO Scientist 2020)
Binary search tree
  1. 18
  2. 6
  3. 17
  4. 20

Ans – (3)

Explanation –

In-order array is 2 3 4 6 7 9 13 15 17 18 20.

Then in-order successor of 15 is 17.

Q27 – The minimum height of an AVL tree with n nodes is
  1. Ceil(log2(n+1)
  2. 1.44log2n
  3. Floor(log2(n+1))
  4. 1.64log2n

Ans – (3)

Explanation – https://compgeek.co.in/avl-tree/ to know more.

 

Q28 – In a file which contains 1 million records and the order of the tree is 100, then what is the maximum number of nodes to be accessed if B+ tree index is used? (ISRO Scientist 2018)
  1. 5
  2. 4
  3. 3
  4. 10

Ans – (2)

Explanation –

Given a file with 1 million records and an order of 100, the height of the B+ tree would be approximately log100(1,000,000) = 4.

The root node is accessed first, then up to 100 nodes at the second level, up to 10,000 nodes at the third level, and up to 1,000,000 nodes at the fourth and final level.

Therefore, the maximum number of nodes to be accessed is 1 (root node) + 100 (second level) + 10,000 (third level) + 1,000,000 (fourth level) = 1,010,101.

Q29 – A priority queue is implemented as a Max-heap. Initially it has 5 elements. The level order traversal of the heap is 10, 8, 5, 3, 2. Two new elements ‘1’ and ‘7’ are inserted into the heap in that order. The level order traversal of the heap after the insertion of the elements is (ISRO Scientist 2017)
  1. 10, 8, 7, 5, 3, 2, 1
  2. 10, 8, 7, 2, 3, 1, 5
  3. 10, 8, 7, 1, 2, 3, 5
  4. 10, 8, 7, 3, 2, 1, 5

Ans – (4)

Explanation –

Max Heap

Its sequence is – 10, 8, 7, 3, 2, 1, 5

Q30 – A strictly binary tree with 10 leaves
  1. cannot have more than 19 nodes
  2. has exactly 19 nodes
  3. has exactly 17 nodes
  4. has exactly 20 nodes

Ans – (2)

Explanation –

If every non-leaf node in a binary tree has nonempty left and right subtrees, the tree is called a strictly binary tree.

A strictly binary tree with n leaves always contains 2n -1 nodes.

Nodes = 10*2 – 1 = 19

Or you can make the tree if you forgot the formula.

Q31 – What is the maximum height of any AVL tree with 7 nodes? Assume that height of tree with single node is 0. (ISRO Scientist 2017)
  1. 2
  2. 3
  3. 4
  4. 5

Ans – (2)

Explanation –

Max height will come when each level contains min nodes.

Minimum Nodes in an AVL tree with height h is

=> N(h) = N(h-1) + N(h-2) + 1

=> N(0) = 1

=> N(1) = 2

=> N(2) = N(1) + N(0) + 1 = 2 + 1 + 1 = 4

=> N(3) = N(2) + N(1) + 1 = 4 + 2 + 1 = 7

So, 7 nodes can have maximum height 3.

Q32 – Which one of the following properties is correct for a red-black tree? (ISRO Scientist 2017)
  1. Every simple path from a node to a descendant leaf contains the same number of black nodes
  2. If a node is red, then one child is red and another is black
  3. If a node is red, then both its children are red
  4. Every leaf node (sentinel node) is red

Ans – (1)

Explanation –

These four requirements must be met by a red-black tree:

The root node is always a black node.

It is believed that a nil is black.

Every red node has black children.

The equal number of black nodes appear on each path from the root to the leaf nodes.

https://compgeek.co.in/red-black-tree/ to know more.

Q33 – Which of the following data structure is useful in traversing a given graph by breadth first search? (ISRO Scientist 2017)
(a) Stack
(b) Queue
(c) List
(d) None of the above

Ans – (2)

Explanation – BFS uses queue data structure. DFS uses stack data structure.

Q34 – A B-Tree used as an index for a large database table has four levels including the root
node. If a new key is inserted in this index, then the maximum number of nodes that could be newly created in the process are (ISRO Scientist 2017)
(a) 5
(b) 4
(c) 1
(d) 2

Ans – (1)

Explanation –

Keys are fully occupied on every level and locations.

Added key arrived.

It turned into a leaf.

An overflow happened.

One key is transferred to the higher level and the leaf is split into two pieces.

Overflow once again. One key is transferred to the higher level, and that component is split into two pieces.

The cycle will repeat until we find the root.

The original root is split into two pieces, and we also have a new root.

Thus, we added one node to each of the ‘n’ layers, as well as a new root.

Therefore, there are n+1 additional nodes overall.  The result is 4+1 = 5.

Q35 – A complete binary tree with n non-leaf nodes contains
  1. n+1 nodes
  2. 2n nodes
  3. 2n+1 nodes
  4. log2n nodes

Ans – (3)

Explanation –

Draw the tree and check.

Q36 – If a node has K children in B tree, then the node contains exactly ___________ keys. (ISRO Scientist 2015)
  1. K2
  2. K -1
  3. K + 1
  4. √K

Ans – (2)

Explanation –

Its very simple, a b tree has a node that contains k ways (children) and has k-1 keys.

 

Q37 – The time complexity of the following C function is (assume n>0)
int recursive (int n) {
if (n==1)
return (1);
else
return (recursive (n-1) + recursive (n-1));
}
  1. O(n)
  2. O(nlogn)
  3. O(n2)
  4. O(2n)

Ans – (3)

Explanation – This code is converted into a numerical equation

=> T(n) = 2T(n-1) + 1

Now you have to solve this equation to find time complexity.

=> T(n) = O(2n).

Q38 – The number of spanning trees for a complete graph with seven vertices is
  1. 25
  2. 75
  3. 35
  4. 22*5

Ans – (2)

Explanation – For a complete graph with n vertices, Cayley’s formula states that the number of spanning trees is n^(n-2). Therefore, for a complete graph with seven vertices, the number of spanning trees is:

7^(7-2) = 7^5 = 16,807

 

Q39 – if one uses straight two-way merge sort algorithm to sort the following elements in ascending order:
20, 47, 15, 8, 9, 4, 40, 30, 12, 17
Then the order of these elements after second pass of the algorithm is (ISRO Scientist 2015)
  1. 8, 9, 15, 20, 47, 4, 12, 7, 30, 40
  2. 8, 15,20,47, 4, 9, 30, 40, 12, 17
  3. 15, 20, 47, 4, 8, 9, 12, 30, 40, 17
  4. 4, 8, 9, 15, 20, 47, 12, 17, 30, 40

Ans – (2)

Explanation –

Merge sort input (Individual Elements) –

20   47   15   8   9   4   40   30   12   17

1st pass (2 elements in an array) –

20 47    8 15    4 9    30 40    12 17

2nd pass (4 elements in an array) –

8 15 20 47     4 9 30 40     12 17

Q40 – The number of rotations required to insert a sequence of elements 9, 6, 5, 8, 7, 10 into an empty AVL tree is? (ISRO Scientist 2013)
  1. 0
  2. 1
  3. 2
  4. 3

Ans – (4)

Explanation – RR, RR, LL rotation done to perform insertion in the AVL tree.

AVL Tree

PREV
NEXT

BOOKS

Algorithm T H CoremanAlgorithm by Udit AgarwalAlgorithm Ellis HorowitzData Structure & Algorithm Made Easy Narasimha

 

GATE Study Material
Previous Year Paper
Subjective Questions