Sorting in linear time
In all the sorting algorithms we have read so far, the worst case is always equal to or greater than nlogn. If we have to reduce the time complexity, then for this we have to increase the space complexity. Because there is no shortage of space, we can give space.
We have three algorithms that solve the time complexity in linear time.
- Counting Sort
- Radix Sort
- Bucket Sort
Counting Sort
Its working is simple but you will forget its working until you practice it 3 or 4 times. This sorting method does not sort by comparing elements. It sorts elements by counting those with unique key values.
- The space complexity is O(n) because we use additional array in the sorting.
- The time complexity is also O(n+k) in the best, average and worst case.
- It uses only integer value
- This algorithm can’t sort negative integers because we are counting the elements from 0 to positive integers, so it is not possible.
- The sort can’t be used as a general-purpose sort because there are many restrictions or constraints in it.
- The largest number in the input array will be used as key ‘k’. Because we have to create an additional array that goes from 0 to k. This sort was named counting sort because we count every key (0, k).
- Example – let’s say input is 5, 1, 9, 25, 100, 3. The highest number is 100, so we have to make the additional array from 0 to 100.
Terms are denoted by
Input array is A[1…n], So Length[A] = n
Output array is B[1…n]
Additional array is C[0…k]

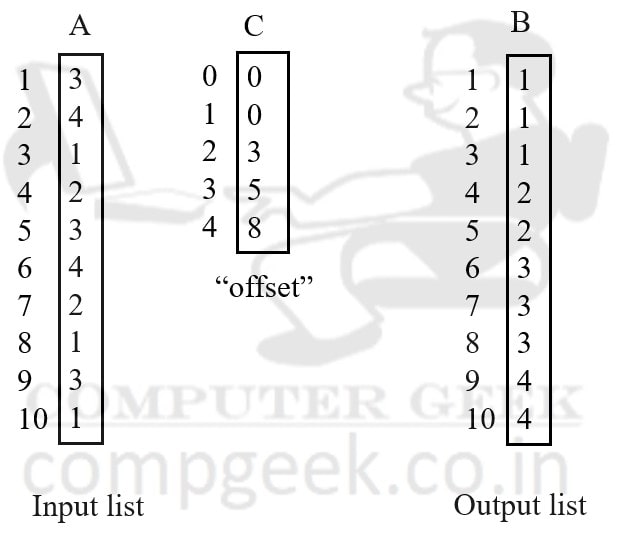
In this diagram, we have taken an input array A, an additional array C and an output array B.
In input array A, the largest number is 4. So, in array C, we only used integers from 0 to 4.
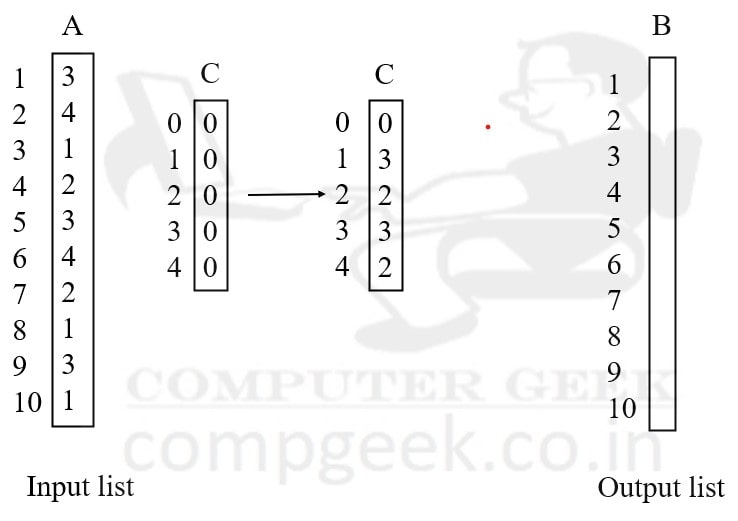
In diagram (b), Array C elements are initialized to 0.
Now counting sort starts.
In array A, the index 1 has a value 3, so in array C, index 3 is incremented by 1. Index 3 = 1.
In array A, the index 2 has a value 4, so in array C, index 4 is incremented by 1. Index 4 = 1.
In array A, the index 3 has a value 1, so in array C, index 1 is incremented by 1. Index 1 = 1.
In array A, the index 4 has a value 2, so in array C, index 2 is incremented by 1. Index 2 = 1.
In array A, the index 5 has a value 3, so in array C, index 3, whose value is 1, is now incremented by 1. Index 3 = 2
In array A, the index 6 has a value 4, so in array C, index 4, whose value is 1, is now incremented by 1. Index 4 = 2
This process is repeated till we cover all indexes of input array A.
Index 0 = 0
Index 1 = 3 because in input, 1 occurs 3 times.
Index 2 = 2 because in input, 2 occurs 2 times.
Index 3 = 3 because in input, 1 occurs 3 times.
Index 4 = 2 because in input, 4 occurs 2 times.
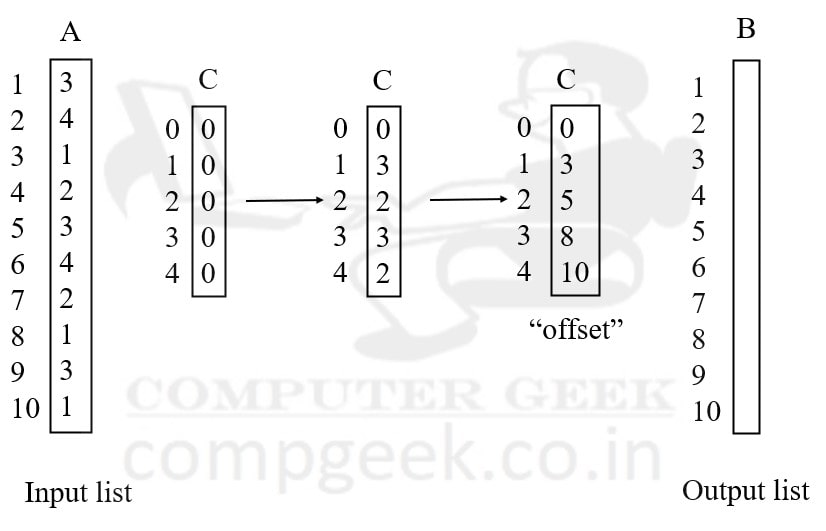
In diagram (C), we took the cumulative sum of array C.
Index 0 value is 0, so the cumulative sum is 0.
Index 1 value is 3, so the cumulative sum is “index 0 value + index 1 value” is 3.
Index 2 value is 2, so the cumulative sum is “index 1 value + index 2 value” is 5.
Index 3 value is 3, so the cumulative sum is “index 2 value + index 3 value” is 8.
Index 4 value is 2, so the cumulative sum is “index 3 value + index 4 value” is 10.
This is called the “offset” stored in array C.
Now we will fill the output sorted list through array A input list and array C offset list.
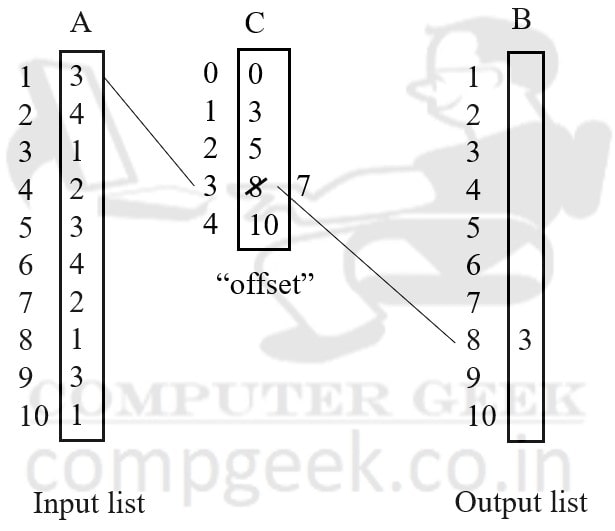
In index 1 of input list, the value is 3.
Now, we will see the value of index 3 of offset list in array C. The value is 8. As a result, set index 8 of the output sorted list to 3. Also, you have to decrement 8 to 7 in the offset list.
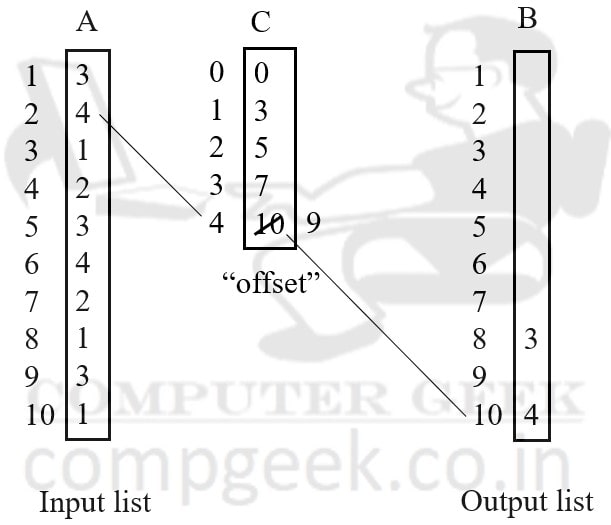
In index 2 of input list, the value is 4.
Now, we will see the value of index 4 of offset list in array C. The value is 10. As a result, set index 10 of the output sorted list to 4. Also, you have to decrement 10 to 9 in the offset list.
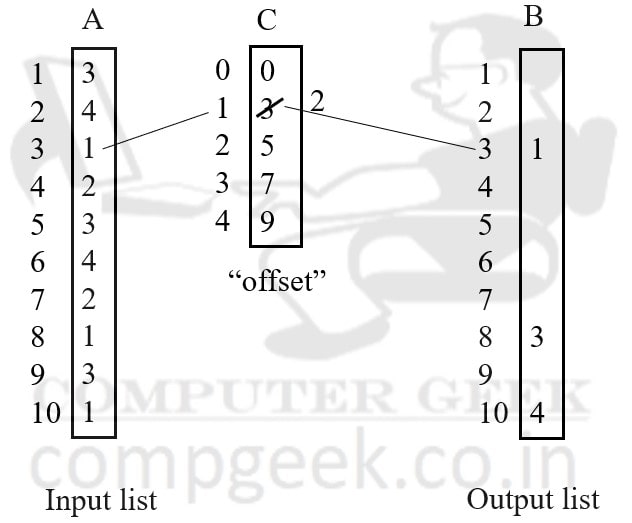
In index 3 of input list, the value is 1.
Now, we will see the value of index 1 of offset list in array C. The value is 3. As a result, set index 3 of the output sorted list to 1. Also, you have to decrement 3 to 2 in the offset list.
Same procedure goes that will fill the output sorted list.
The result is
CountingSort(A[1…n], max, C[0…max])
- Enter the input array A[1…n].
- Take out the maximum number in input array.
- In array C, declare from 0 to maximum of A[] and initialize with 0.
- for i <- 1 to n
C[A[i]]++;
- for j <- 1 to max
C[j] = C[j] + C[j-1]
- for i <- 1 to n
B[C[A[i]]] = A[i]
- C[A[i]]–;
- Enter the input array A[1…n].
- Take out the maximum number in input array.
- In array C, declare from 0 to maximum of A[] and initialize with 0.
Enter an input array A from 1 to n index. Take the maximum number in the array. Let’s say that index 1 is maximum. After that, you will compare all the indices with the maximum you choose, and if any index has a greater value, then point to that index.
From 0 to the maximum of array A, declare an array and name it C (Count).
- for i <- 1 to n { C[A[i]]++; }
Traverse over all of the elements in Array A. There is some value in all the indexes. Take the value and move over to array C. The input array value is turned into an index in the count ‘C’ array. So, all you have to do is increase the value of that index in the count array by 1.
- for j <- 1 to max { C[j] = C[j] + C[j-1]; }
Find the cumulative sum of the count array.
Index 1 -> index 0 + index 1
Index 2 -> index 1 + index 2, and so on…
- for i <- 1 to n
{ B[C[A[i]]] = A[i]; }
You need to perform B[C[A[i]] = A[i] from index 1 to index n.
This B[C[A[i]] appears to be difficult, but it is not. We chose a value i say 1.
A[i] denotes the value at index 1 of the input array.
C[A[i]] denotes that the value has an index in array C that has a value.
B[C[A[i]] denotes that the value in array C has an index in sorted output array B, and the value of that index is A[i].
Program of Counting Sort in C
// Write a program for Counting Sort
// COMPUTER GEEK – compgeek.co.in
// Write a program for Counting Sort
#include<stdio.h>
int main()
{
int A[100], C[100] = {0}, B[100], size, i, j, max=0;
//Input array declaration
printf(“Enter the size of the array : “);
scanf(“%d”, &size);
//Input array initialiazation
printf(“Enter the %d item of the array b/w 0 to 100 : “, size);
for(i=1; i<=size; i++)
{
scanf(“%d”, &A[i]);
if(A[i] > max)
{
max = A[i];
}
}
//Filling up of array ‘C’
for(i=1; i<=size; i++)
{
C[A[i]] = C[A[i]] + 1;
}
//Cumulative Sum of Count ‘C’ array
for(j=1; j<=max; j++)
{
C[j] = C[j]+C[j-1];
}
//fill array ‘B’ with array ‘A’ and ‘C’
for(i=1; i<=size; i++)
{
B[C[A[i]]] = A[i];
C[A[i]]–;
}
//Array After counting sort
printf(“\nThe Sorted Array B is : “);
for(i=1; i<=size; i++)
{
printf(“%d “,B[i]);
}
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Counting Sort
import java.util.Scanner;
public class CountingSort
{
public static void main(String[] args)
{
Scanner scanner = new Scanner(System.in);
int[] A = new int[100];
int[] C = new int[100];
int[] B = new int[100];
int size, i, j, max = 0;
// Input array declaration
System.out.print(“Enter the size of the array : “);
size = scanner.nextInt();
// Input array initialization
System.out.print(“Enter the ” + size + ” items of the array between 0 to 100 : “);
for (i = 1; i <= size; i++)
{
A[i] = scanner.nextInt();
if (A[i] > max)
{
max = A[i];
}
}
// Filling up of array ‘C’
for (i = 1; i <= size; i++)
{
C[A[i]] = C[A[i]] + 1;
}
// Cumulative Sum of Count ‘C’ array
for (j = 1; j <= max; j++)
{
C[j] = C[j] + C[j – 1];
}
// Fill array ‘B’ with array ‘A’ and ‘C’
for (i = 1; i <= size; i++)
{
B[C[A[i]]] = A[i];
C[A[i]]–;
}
// Array After counting sort
System.out.print(“\nThe Sorted Array B is : “);
for (i = 1; i <= size; i++)
{
System.out.print(B[i] + ” “);
}
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for Counting Sort
def main():
A = [0] * 100
C = [0] * 100
B = [0] * 100
max_val = 0
# Input array declaration
size = int(input(“Enter the size of the array : “))
# Input array initialization
print(“Enter the”, size, “items of the array between 0 to 100 : “)
for i in range(1, size + 1):
A[i] = int(input())
if A[i] > max_val:
max_val = A[i]
# Filling up of array ‘C’
for i in range(1, size + 1):
C[A[i]] = C[A[i]] + 1
# Cumulative Sum of Count ‘C’ array
for j in range(1, max_val + 1):
C[j] = C[j] + C[j – 1]
# Fill array ‘B’ with array ‘A’ and ‘C’
for i in range(size, 0, -1):
B[C[A[i]]] = A[i]
C[A[i]] -= 1
# Array After counting sort
print(“\nThe Sorted Array B is :”, end=” “)
for i in range(1, size + 1):
print(B[i], end=” “)
if __name__ == “__main__”:
main()
Time & Space Complexity of counting sort
In best, average & worst case, time complexity is O(n+k),
Where n is no of input and k is the maximum number in the input.
Space complexity is O(n+k), because B array contain n values and C array contain k values.
It contains a main array and an auxiliary (additional) array to perform the sort.
Advantages of counting sort
- Time complexity is very less O(n + k).
- Easy to code.
- It is a stable sort.
Disadvantages of counting sort
- This sort is not used for non-integer numbers.
- If the value of k is very high, then choosing counting sort is not sensible.
- Working is simple but there are several procedures which make it difficult.
Test Yourself
Q1- Explain the working principle of counting sort.
Counting sort is a linear time sorting algorithm that doesn’t compare elements but sorts them by counting the occurrences of unique key values. It works by first counting the occurrences of each key in the input array and then using this count information to place the elements in their sorted order. It requires an additional count array to store the counts and an output array to hold the sorted elements.
Q2- What is the time complexity of counting sort in the best, average, and worst cases?
The time complexity of counting sort is O(n + k) in all cases, where n is the number of elements in the input array and k is the range of the input (maximum element – minimum element + 1).
Q3- Explain the limitations of counting sort.
- Counting sort is not suitable for sorting non-integer values, as it relies on integer keys to count occurrences.
- It also becomes inefficient if the range of elements (k) is significantly larger than the number of elements (n) in the input array.
- Moreover, it is not a comparison-based sorting algorithm and cannot be used with custom comparison functions.2
- It is used in a very limited number of real problems. (Why?). It says that its time complexity is linear, but for a linear time, its space complexity is much higher O(n+k). you have to make a new array to build counting sort. and if k is larger then there is no point to applying this algorithm.
Q4- How does counting sort handle duplicate elements during the sorting process?
Counting sort handles duplicate elements by counting their occurrences in the input array. The count array stores the frequency of each element, and during the output phase, it correctly places duplicate elements in their respective positions in the sorted output array while maintaining their relative order.
Q5- What is the space complexity of counting sort?
The space complexity of counting sort is O(n + k), where n is the number of elements in the input array and k is the range of the input (maximum element – minimum element + 1). It requires additional space for the count array and the output array.
Q6- Explain why counting sort is considered a stable sorting algorithm.
Counting sort is considered stable because it preserves the relative order of elements with equal keys. When counting the occurrences of elements, it places elements with equal keys in the output array in the same order as they appeared in the input array.
Q7- Can counting sort be used to sort an array containing negative integers? Why or why not?
No, counting sort cannot be directly used to sort an array containing negative integers. Counting sort relies on non-negative integer keys to count occurrences, so negative integers would not fit this criterion. However, with some preprocessing, such as shifting the array to make all elements positive, counting sort could be adapted for arrays with negative integers.
Q8- What is the main advantage of counting sort compared to other sorting algorithms?
The main advantage of counting sort is its linear time complexity, O(n + k), which makes it highly efficient for sorting large datasets with a relatively small range of elements. It is particularly useful when the range of elements is not significantly larger than the number of elements in the array.
Q9- Describe the steps involved in implementing counting sort.
The steps involved in implementing counting sort are as follows:
- Find the range (max – min) of elements in the input array.
- Create an additional count array C with a size equal to the range + 1, initialized with zeros.
- Count the occurrences of each element in the input array and store them in the count array C.
- Modify the count array to contain the cumulative sum of counts (offsets).
- Create the output array B of the same size as the input array.
- Traverse the input array and place each element in its correct sorted position in the output array B based on the count array C.
- Decrement the count in the count array for each occurrence of an element to handle duplicates correctly.
Q10- Counting sort is based on
Comparison of elements
Counting occurrences of unique key values
Searching for the minimum and maximum elements
Rearranging elements based on their indices
Ans – (2)
Explanation – Counting sort works by counting occurrences of unique key values in the input array to sort elements.
Q11- What is the time complexity of counting sort in the worst case?
O(1)
O(n)
O(nlogn)
O(n + k)
Ans – (4)
Explanation – The time complexity of counting sort in the worst case is O(n + k), where n is the number of elements in the input array and k is the range of the input.
Q12- What type of data can counting sort handle?
Integer values only
Non-integer values only
Custom data types
Both integer and non-integer values
Ans – (1)
Explanation – Counting sort can only handle integer values as it relies on integer keys to count occurrences.
Q13- Why is counting sort not suitable for sorting arrays with a large range of elements?
It has a high time complexity
It is not a stable sorting algorithm
It requires additional space for sorting
It may result in significant memory usage and inefficiency
Ans – (4)
Explanation – Counting sort may not be suitable for sorting arrays with a large range of elements (k) as it can lead to significant memory usage and inefficiency.
Q14- Counting sort can be used as a general-purpose sorting algorithm for:
Integer values
Non-integer values
Small datasets
Large datasets
Ans – (3)
Explanation – Counting sort can be used as a general-purpose sorting algorithm for arrays containing integer values.
Q15- In counting sort, the count array stores:
Sorted elements
Occurrences of each element
Cumulative sum of elements
Indices of elements
Ans – (2)
Explanation – In counting sort, the count array stores the occurrences of each element in the input array.






