Complexity Classes

Introduction

.

In the field of algorithms, understanding how efficiently an algorithm solves a problem is crucial. This is where complexity classes come into play. Complexity classes group problems based on the resources (time and space) required to solve them. In simple terms, they help us understand how “hard” a problem is and what kind of algorithms can solve it.

In this post, we will discuss the major complexity classes in the context of time complexity (how long it takes for an algorithm to run), such as P, NP, NP-Complete, and NP-Hard. These classes form the foundation for analyzing algorithms in computer science.

.

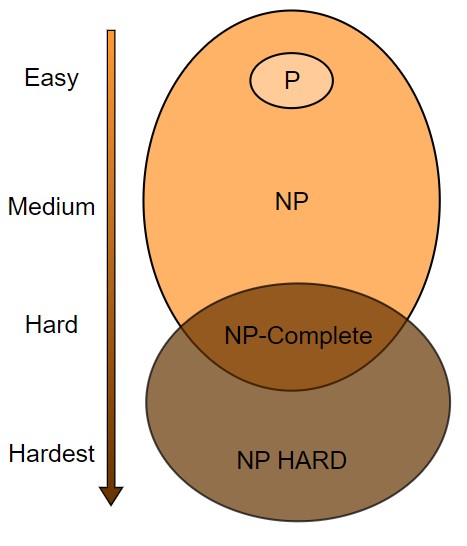
Complexity Classes

1. Class P Problem (Polynomial Time)

Problems in class P are those that can be solved by an algorithm in polynomial time. In other words, the time taken to solve these problems grows at a polynomial rate as the input size increases.

Polynomial time algorithms are considered efficient and practical for real-world use. If a problem is in class P, it means we can solve it relatively quickly even for large inputs.

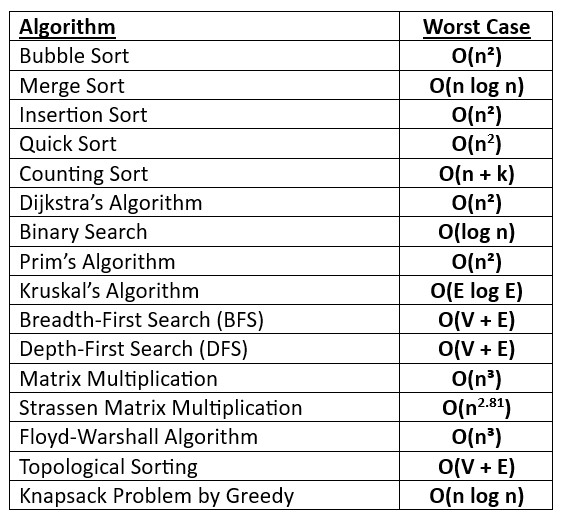
Examples of Polynomial Time Algorithms

.

2. Class NP (Nondeterministic Polynomial Time)

Problems in class NP are those where a solution can be verified in polynomial time, but we don’t necessarily know how to solve them efficiently.

The key idea here is that if someone gives us a solution, we can check if it’s correct in a reasonable amount of time.

NP problems are crucial because they are often more challenging to solve but still easy to verify. Easy means Polynomial time.

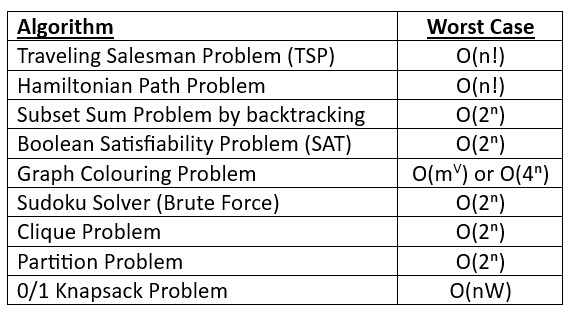
Examples of Non-Polynomial Time Algorithms

.

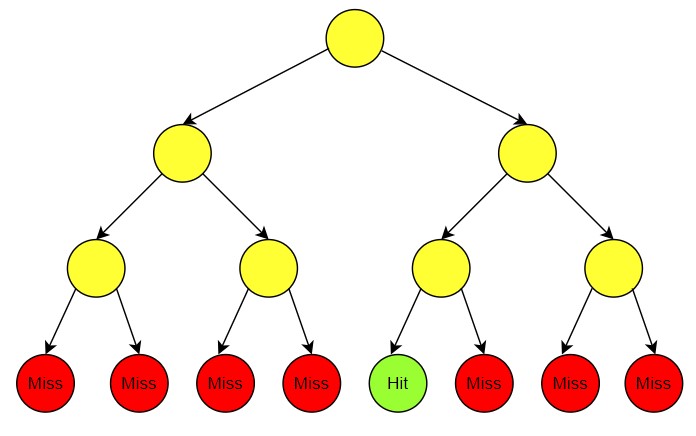
In the image, the tree represents different potential paths for solving a problem which is in NP. Solving it requires O(2ⁿ) time.

However, if someone gives you the correct solution (like the “Hit” in the tree), verifying that it’s correct is much simpler. You only need to check the path and see if it satisfies all the rules or conditions of the problem.

A language L is considered to be NP if and only if a polynomial-time verification algorithm for it exists. Keep in mind that P ⊆ NP. We are now unsure of whether P = NP or P ⊂ NP.

This NP class also introduces us to the famous P vs NP problem, a major unsolved question in computer science: “Is every NP problem also in P?” In simpler terms, can every problem whose solution is easy to check also be solved quickly?

You can read about this in the next post. Full details are provided.

.

3. NP-Hard Problems

NP-Hard problems are at least as hard as the hardest problems in NP, but they may not even belong to class NP.

We could develop an algorithm to solve the problem, but once it’s executed, it keeps running endlessly without ever stopping. That would only happen if you use a large input for a given problem.

Example

1. If you’re trying to solve a traveling salesman problem and you input 1000 cities, expecting to get a solution, it won’t happen. You’ve essentially set the program to run indefinitely, and it will take about 2⁴⁰ years to solve if you have a super computer.
2. Scheduling a Family Gathering is an NP-hard problem. When organizing a gathering for many family members, each with their own availability, it becomes increasingly difficult to find a time that works for everyone. While it’s easy to accommodate a few people, as the number of participants grows, the combinations of schedules become exponentially complex, making it challenging to find the best solution.

.

The Travelling Salesman Problem is as hard as the hardest problem in NP. If we take large input, then we can say that it is NP Hard.

Also, the examples of NP problem are hard problem, if we take large input.

So, how can we say that all the problem written above are NP-Hard?

We can say this thing with the help of Reduction.

.

What is Reduction ?

Reduction is a concept used in computer science to compare the complexity of different problems. It refers to the process of transforming one problem into another in such a way that a solution to the second problem can be used to solve the first.

If a problem A can be reduced to problem B, it means that solving problem B would allow us to solve problem A as well.

Also, we know that Boolean Satisfiability Problem (SAT) is NP-Hard. So, if we can say that Boolean Satisfiability Problem (SAT) can be reduced to Hamiltonian Path Problem, it means that solving Hamiltonian Path Problem would allow us to solve Boolean Satisfiability Problem (SAT) as well.

To find the relationship between the problems, we are using polynomial time reduction.

.

Polynomial Time Reductions

There exists a polynomial-time computable function f that maps any instance of problem A to an instance of problem B. That is, given an instance x of problem A, the function f(x) produces an instance of problem B.

The answer to the instance x of problem A is the same as the answer to the transformed instance f(x) of problem B. More formally, for any instance x of problem A

x ∈ A  ⟺  f(x) ∈ B

This means that if x is a “yes” instance of decision problem A, then f(x) is a “yes” instance of decision problem B, and if x is a “no” instance of A, then f(x) is a “no” instance of B.

So, Boolean Satisfiability Problem (SAT) is NP-Hard and it is reducing to Hamiltonian Path Problem in polynomial time. So, Hamiltonian Path Problem is NP-Hard.

Boolean Satisfiability Problem (SAT) ∝ Hamiltonian Path Problem

The same way, we can reduce to other problems also by taking polynomial time.

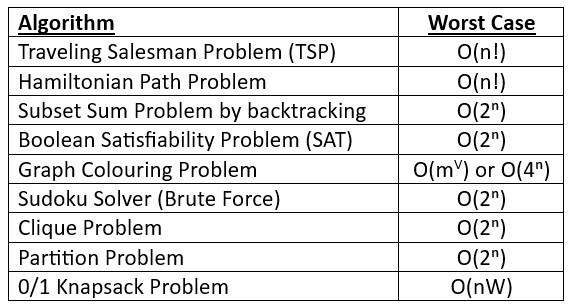
SAT ∝ Subset Sum Problem

SAT ∝ Travelling Salesman Problem

SAT ∝ Graph Colouring Problem

SAT ∝ Sudoku Solver

SAT ∝ Clique Problem

SAT ∝ Partition Problem

SAT ∝ 0/1 Knapsack Problem

So, every problem we mentioned here is the hardest problem and it is a problem of NP-Hard Class.

.

4. NP-Complete Problems

A problem A is NP-Complete if it satisfies two properties

• For every problem B ϵ NP, problem B can be reduced to problem A in polynomial time (A is NP-Hard).
• Problem A is in NP means a non-deterministic algorithm can be written for a problem A.

If the Problem satisfies the property (1) only, then it is an NP-Hard Problem. If the problem satisfies both the properties mentioned here, then it is an NP-Complete Problem.

.

Further, we must look upon some problem that is an NP-hard problems but not NP-complete.

1. Halting Problem is an undecidable Problem and is also proved by Alan Turing. It is not in NP.
2. Graph Isomorphism Problem is not yet classified as NP- Complete Problem.
3. Post Correspondence Problem (PCP) is an undecidable language.
4. Integer Programming involves finding integer solutions to a system of linear equations or inequalities.
5. Minimum Circuit Size Problem asks for the smallest Boolean circuit that can compute a given Boolean function.