Clique Problem

Introduction

.

The Clique Problem is a well-known problem in computer science and graph theory.

This problem is important in the study of NP-completeness because it is one of the NP-complete problems. This means that no fast (polynomial-time) solution is known for it, and it is as hard as any problem in the NP class.

But before going any further, we have to see what a complete graph is?

.

Definition of Complete Graph 

A graph is called a complete graph if every pair of distinct vertices is connected by an edge. A complete graph with n vertices is denoted by K_n. In a complete graph, every possible edge between vertices exists.

.

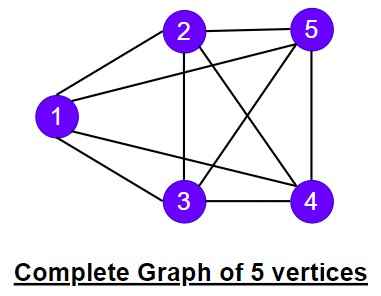
Here is a complete graph of 5 vertices and every pair of distinct vertices is connected by an edge. The number of edges in a complete graph is n(n -1)/2, where n is the number of vertices.

.

Question – Examine the provided graph with 5 vertices. Is this graph a complete graph, meaning every pair of vertices is connected by an edge?

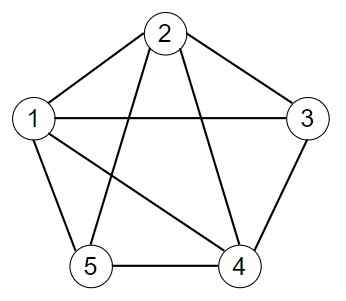
The vertex 5 is not connected to vertex 3. Hence, it is said that this graph not a complete graph.

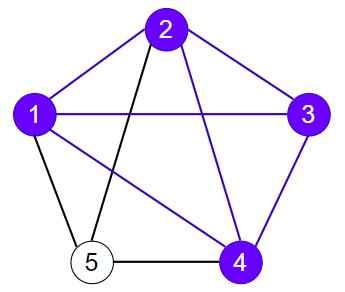
But a subgraph {1, 2, 3, 4} is said to be a complete graph in which all the pairs are connected by an edge.

A subgraph that forms a complete graph is called a clique. In this case, using the brute force algorithm, we have identified a 4-clique within the 5-vertex graph. This means that the subgraph formed by 4 vertices is fully connected, with every pair of vertices having an edge between them, making it a complete graph.

We can find that the 4 vertices are fully connected, which means it forms a maximum clique. This maximum clique includes all four vertices. Additionally, there are several fully connected 3-vertex combinations, such as {(1, 2, 3), (2, 3, 4), (1, 2, 4), (1, 3, 4)}. Furthermore, we can identify fully connected pairs of 2-vertices {(1, 2), (2, 3), (3, 4), (1, 3), (1, 4), (2, 4)}.

.

Classification of Clique Problem

The Clique Problem can be presented in various ways, depending on the specific cliques and the information needed about them. Common variations of the problem include

1. Identifying the maximum clique (the largest clique in terms of vertex count)
2. Finding the maximum weight clique in a weighted graph
3. Listing all maximal cliques
4. The decision problem of determining whether a graph has a clique of size k.

.

Question – Can you find the maximum clique in the below graph?

Not in the polynomial time, because it is a very very hard problem. Let define it.

.

Clique Optimization Problem (COP) Statement

Given an undirected graph G = (V, E), the objective of the Clique Optimization Problem is to find the largest clique in the graph. A clique is a subset of vertices where every two distinct vertices are connected by an edge. The goal is to maximize the number of vertices in this fully connected subset.

The Clique Optimization Problem belongs to the class NP-Hard. This means that while finding the largest clique is difficult (no known polynomial-time algorithm exists to solve it).

.

Clique Decision Problem (CDP) Statement

Given an undirected graph G = (V, E) and an integer k, the problem is to determine whether there exists a clique of size k in the graph. In other words, the task is to decide if there is a subset of k vertices such that every pair of vertices in this subset is connected by an edge.

This problem asks for a yes or no answer to whether the graph contains a clique of at least k vertices and is classified as NP-complete.

.

History

The term “clique” in graph theory was first coined by the Hungarian mathematician Pál Turán in the 1940s. The term was inspired by its sociological meaning, where a “clique” refers to a group of individuals who are all connected with each other.

The Clique Decision Problem was classified as NP-complete by Richard Karp in his 1972 paper, where he identified 21 NP-complete problems.

.

Reduction from SAT to Clique

The Boolean Satisfiability Problem (SAT) can be polynomially reduced to the Clique Decision Problem. This means that if we can solve the Clique Decision Problem efficiently (in polynomial time), then we can also solve 3-SAT efficiently, implying that the Clique Decision Problem is at least as hard as 3-SAT.

To construct a reduction from the Boolean Satisfiability Problem (3-SAT) to the Clique Decision Problem, let’s go through an example step-by-step.

.

Algorithm 3-SAT_to_Clique(SAT_formula)

1. Input a Boolean Formula in CNF. The CNF formula consists of m clauses, each with n literals.
2. Initialize an empty graph G = (V, E). Each literal from each clause in the formula is represented by a vertex.
3. For each literal in each clause, create a vertex in the graph. Let vij represent the jth literal in the ith clause.
4. Add edges between two vertices from different clauses if the literals are not contradictory. Two literals are contradictory if one is the negation of the other (e.g., x1​ and ¬x1​).
5. Check for a clique of size m (number of clauses). A clique is a set of vertices where every pair of vertices is connected by an edge.
6. If G contains a clique of size m

           Return True // 3-SAT_formula is satisfiable

       Else:

           Return False // 3-SAT_formula is unsatisfiable

.

Example –

Consider the following Boolean formula

F = (x1​ ∨ ¬x2​ ∨ x3​) ∧ (x2​ ∨ x3​ ∨ ¬x4​) ∧ (¬x1​ ∨ ¬x3​ ∨ x4​)

Step 1 – The clauses is 3 and there are 3 literals in each clause.

Step 2 – Create a graph

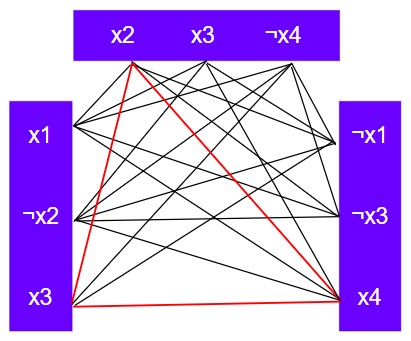
Step 3 – Add edges between two vertices from different clauses if the literals are not contradictory.

Step 4 – In this graph, there are many valid cliques of size 3, but I choose the red colored clique. 

If such a clique exists, it means that there is a set of literals, one from each clause, that are all mutually consistent and satisfy the original SAT formula.

Since 3-SAT can be reduced to the Clique Decision Problem in polynomial time, the Clique Decision Problem is at least as hard as 3-SAT. Given that 3-SAT is NP-complete, this shows that the Clique Decision Problem is also NP-complete.

.

If we can say that SAT can be reduced to Clique Problem, it means that solving Clique Problem would allow us to solve SAT as well.

Let’s verify from the above example. The clique problem is solved and we need to solve SAT problem by the vertices of clique.

In the figure, the vertices labelled in red, which form a triangle, represent specific assignments of the variables –

• No x1 means x1 = either True or False. So, we take x1 = false because of the worst case.
• x2 means x2 = True.
• x3 means x3 = True.
• X4 means x4 = True.

These assignments illustrate how the variables are set to satisfy the constraints in the problem.

F = (x1​ ∨ ¬x2​ ∨ x3​) ∧ (x2​ ∨ x3​ ∨ ¬x4​) ∧ (¬x1​ ∨ ¬x3​ ∨ x4​)

F = (False V False V True) ∧ (True V True V False) ∧ (True V False V True)

F = True ∧ True ∧ True

F = True

Hence, SAT Problem is true. it means that solving Clique Problem would allow us to solve 3-SAT as well.