Design & Analysis of Algorithm logo
in Hindi

Christofides Algorithm (TSP)

PREV
NEXT
Distribute Education like Computer Geek
Menu

Introduction

.

The Traveling Salesman Problem (TSP) is a classic problem in computer science and mathematics. The goal is to find the shortest possible route that allows a salesman to visit each city exactly once and return to the starting city.

It’s a problem that can be solved using different methods, and one effective approach is the Christofides Algorithm.

The TSP can be solved using various methods

  1. Brute Force – Check all possible routes and choose the shortest one. This method guarantees the optimal solution but is impractical for large datasets due to its high computational cost.
  2. Greedy Algorithms – Heuristics that make local optimal choices at each step to find a global optimum. It is also called Nearest Neighbour Problem.
  3. Dynamic Programming – Optimizes the problem by solving subproblems and combining their solutions. It is also called Held-Karp algorithm.
  4. Branch & Bound Approach – breaking the problem into smaller subproblems (branching) and calculating a lower bound for each subproblem. If the lower bound exceeds the current best solution, that branch is pruned (ignored).
  5. Approximation Algorithms – Provides near-optimal solutions in a reasonable time, useful for large instances. It is also called Christofides Algorithm.

We first solve the Travelling Salesman Problem by Greedy algorithm, then solve by Dynamic Programming and now we are solving it by approximation algorithm and the problem name is Christofides Algorithm. It provides an approximation solution guaranteeing that the solution is at most 1.5 times the optimal solution.

.

Problem Statement

Given a set of n cities and the distances between every pair of cities, the objective is to find a near-optimal tour using the Christofides algorithm. The tour should start from one city, visit each city exactly once, and return to the starting city, such that the total travel cost is as small as possible.

  1. The number of cities (n ≥ 3).
  2. A distance matrix dist[][] where dist[i][j] represents the distance between city i and city j.
  3. The total cost of the tour, which will be at most 1.5 times the optimal solution.

.

History of the Christofides Algorithm

The Christofides algorithm was introduced by Nicos Christofides, a British-Cypriot mathematician, in 1976. The algorithm is designed to provide an approximate solution to the Traveling Salesman Problem (TSP), specifically for the metric TSP, where the triangle inequality holds (i.e., the direct path between two cities is never longer than going through an intermediate city).

Christofides developed a 3-step approximation algorithm that guarantees a solution within 1.5 times the optimal cost for metric TSP. This was a significant improvement over previous algorithms, as it combined graph theory concepts like Minimum Spanning Tree (MST) and Eulerian circuits with perfect matching to achieve this approximation ratio.

Even today, no algorithm has been found that consistently beats the 1.5 approximation factor for the metric TSP. Christofides work continues to influence modern algorithmic research in graph theory and combinatorial optimization.

.

Christofides Algorithm
  1. Start by constructing an MST from the graph that connects all cities with the minimum possible total edge weight. An MST ensures that all cities are connected but doesn’t ensure a tour.
  2. In the MST, find all vertices with an odd degree (an odd number of edges). According to graph theory, an MST will always have an even number of odd-degree vertices.
  3. Perform a minimum weight perfect matching on the odd-degree vertices. In a perfect matching, each odd-degree vertex is connected to another odd-degree vertex using the least possible edge weight from the original graph.
  4. Combine the edges of the MST and the matching to form a multigraph. This graph now has a Eulerian circuit, where each vertex has an even degree.
  5. Find a Eulerian circuit in the combined graph. A Eulerian circuit is a cycle where every edge is visited exactly once.
  6. Convert the Eulerian circuit into a Hamiltonian cycle (a cycle where each vertex is visited exactly once) by skipping repeated vertices.

.

Example

Let’s walk through Christofides algorithm step by step using the provided distance matrix between six cities – A, B, C, D, E, and F. In the graph, triangle inequality holds (i.e., the direct path between two cities is never longer than going through an intermediate city).

.

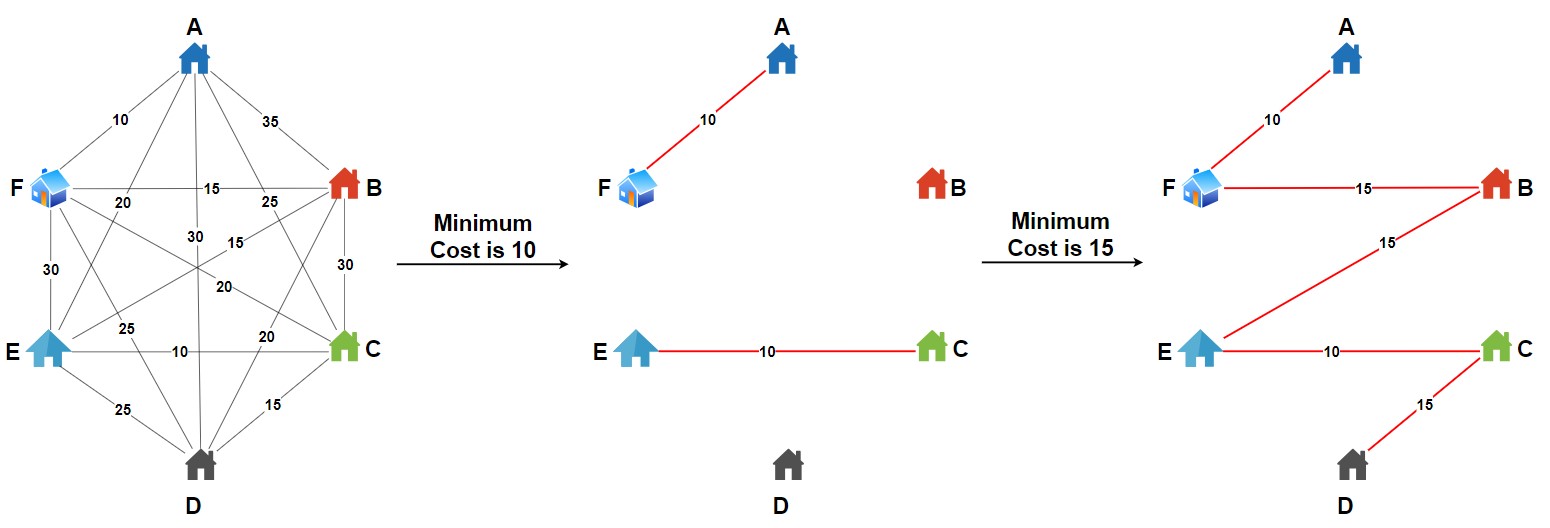
Step 1 – We first need to find the Minimum Spanning Tree of the graph. This tree must connect all cities with the minimum total edge weight.

We will use Kruskal’s algorithm to find the MST.

Christofides Algorithm MST

.

So, we have found an MST and its path are A -> F -> B -> E -> C -> D

Total Cost is 65.

.

Step 2 – Find Odd-Degree Vertices (Vertices with an odd number of edges).

Next, we identify the vertices in the MST with an odd degree.

  • City A has degree 1 (odd).
  • City D has degree 1 (odd).

.

Step 3 – Perform a minimum weight perfect matching on the odd-degree vertices.

There is only one edge between city A to city D and that cost is 30. We can’t have B, C, E and F in between A and D, because they are even degree vertices. Each odd-degree vertex is connected to another odd-degree vertex using the least possible edge weight from the original graph.

City A -> City D and its Cost = 30.

.

Step 4 – Combine the edges of the MST and the minimum weight perfect matching to form a multigraph.

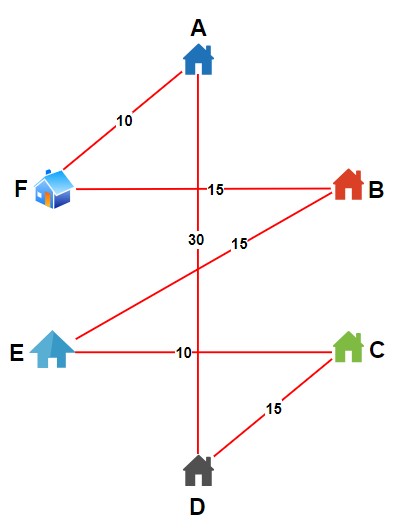
Christofides Algorithm MST + matching

.

Step 5 – A Eulerian circuit is a path that visits every edge exactly once. Since this graph has all even-degree vertices, we can find such a circuit.

A -> F -> B -> E -> C -> D -> A

.

Step 6 – Finally, we convert the Eulerian circuit to a Hamiltonian tour by visiting each city only once (except the starting city).

A -> F -> B -> E -> C -> D -> A

The Hamiltonian tour is A → F → B → D → E → C → A with a total cost of 95.

This is under 1.5-approximation of the optimal solution using the Christofides algorithm.

.

Source Code of Christofides Algorithm

Time Complexity of Christofides Algorithm
  1. Prims or Kruskal’s Algorithm (MST Calculation) takes O(E logV) where E is the number of edges and V are the number of vertices.
  2. Finding Odd Degree Vertices iterates through the edges of the MST and counts the degree of each vertex. It takes O(V) time.
  3. Minimum Weight Matching on Odd Degree Vertices takes O(V2) time.
  4. Constructing the Eulerian circuit from the MST and matching edges takes O(V+E).
  5. Constructing the Hamiltonian path from the Eulerian circuit is done in O(V).

Summing all the time complexities O(Elog V + V + V2 + V + E + V) will result O(Elog V + V2).

For a complete graph (which is typical in TSP), E=V(V−1)/2, in the worst case, this becomes O(V2logV).

.

Space Complexity of Christofides Algorithm

The adjacency matrix used to represent the graph takes O(V2) space, since we need to store weights for each pair of vertices.

.

Advantages of Christofides Algorithm
  1. Approximation Guarantee
    • Christofides’ algorithm provides a 3/2-approximation for the Traveling Salesman Problem (TSP) in metric spaces, ensuring the solution is at most 1.5 times the optimal cost.
  2. Polynomial Time Complexity
    • The algorithm runs in polynomial time, making it suitable for larger instances of TSP where exact solutions are computationally infeasible.
  3. Works for Metric TSP
    • It is effective for metric TSPs, where distances satisfy the triangle inequality, applicable to many real-world routing and logistics problems.
  4. Combines Greedy and Matching Approaches
    • By combining Kruskal’s greedy algorithm with minimum weight perfect matching, it efficiently forms an Eulerian circuit, balancing solution quality and computational efficiency.
  5. Practical for Real-World Applications
    • Suitable for applications in vehicle routing, logistics, and network optimization where near-optimal solutions are desired.
  6. Easy to Implement
    • The algorithm uses well-known techniques like MST and matching, making it relatively straightforward to code and understand.
  7. Edge Case Handling
    • It effectively handles odd-degree vertices through matching techniques, ensuring the Eulerian circuit can be formed.
  8. Widely Used for Heuristics
    • Many practical heuristics for TSP use Christofides’ algorithm as a foundation due to its balance between efficiency and accuracy.

.

Disadvantages of Christofides Algorithm
  1. Approximation Limitations
    • While it guarantees a solution within 1.5 times the optimal cost, this may not be acceptable for applications requiring exact solutions.
  2. Assumption of Metric Space
    • The algorithm is designed for metric spaces where distances satisfy the triangle inequality, limiting its applicability to certain types of problems.
  3. Complexity for Non-Metric Problems
    • For TSP instances that do not conform to metric properties, the algorithm may not provide useful results or can be inefficient.
  4. Additional Computation Overhead
    • The combination of finding a Minimum Spanning Tree and performing minimum weight matching can introduce additional computational overhead compared to simpler heuristics.
  5. Handling Large Graphs
    • Although it is polynomial in time complexity, the algorithm may still struggle with very large graphs due to the inherent complexity of the MST and matching steps.
  6. Implementation Challenges
    • While conceptually straightforward, the implementation of various components like matching can be complex and error-prone, especially for beginners.

.

Applications of Christofides Algorithm in Real Life
  1. Logistics and Supply Chain Management
    • Used for optimizing delivery routes for trucks and vehicles, reducing transportation costs and improving efficiency in logistics operations.
  2. Vehicle Routing
    • Helps in planning routes for garbage collection, public transportation, and delivery services to minimize travel distance and time.
  3. Telecommunications
    • Applied in designing efficient network layouts and routing for data packets, ensuring minimal latency and reduced transmission costs.
  4. Manufacturing and Production
    • Used in scheduling and routing tasks within manufacturing processes to optimize workflow and resource allocation.
  5. Tourism and Travel Planning
    • Assists in creating optimal travel itineraries for tourists, ensuring that multiple destinations are visited in the shortest possible route.
  6. Robotics
    • Utilized in path planning for autonomous robots, enabling them to navigate efficiently in environments with multiple points of interest.
  7. Computer Graphics
    • Helps in rendering and traversing graphical data structures where optimal paths need to be computed, enhancing visual performance.
  8. Urban Planning
    • Applied in the design of urban transport systems and public amenities to ensure efficient connectivity and accessibility across cities.
  9. Energy Distribution
    • Used in optimizing routes for power line maintenance and monitoring, ensuring minimal travel distance for utility vehicles.
  10. Air Traffic Management
    • Helps in optimizing flight paths and scheduling for airlines, reducing fuel consumption, and improving overall operational efficiency.
PREV
NEXT

Test Yourself

Q1- Why is the Traveling Salesman Problem (TSP) considered NP-hard?

TSP is considered NP-hard because no polynomial-time algorithm is known that can solve it exactly for all possible inputs. The number of possible tours grows factorially with the number of cities, making the problem computationally intractable for large instances.

Q2- How does the Christofides algorithm guarantee an approximation of 1.5 times the optimal solution?

The Christofides algorithm constructs a Minimum Spanning Tree (MST), performs a minimum weight matching on odd-degree vertices, and then forms an Eulerian circuit, ensuring that the final Hamiltonian cycle costs no more than 1.5 times the optimal solution in metric TSP.

Q3- Explain the role of Minimum Spanning Tree (MST) in the Christofides algorithm.

The MST connects all cities with the minimum total edge weight without forming cycles. It is the first step in Christofides algorithm, which serves as a base for adding the extra edges needed to complete a tour.

Q4- Why does the Christofides algorithm only work for metric TSP problems?

Christofides relies on the triangle inequality, which holds in metric spaces, ensuring that the direct path between two cities is never longer than a detour through an intermediate city. This property is essential for the algorithm to achieve its 1.5 approximation guarantee.

Q5- What is the significance of odd-degree vertices in the Christofides algorithm?

In an MST, there is always an even number of vertices with an odd degree. These odd-degree vertices must be paired using a minimum weight matching to ensure that the final Eulerian circuit can be converted into a Hamiltonian cycle.

Q6- What is the role of Eulerian circuits in the Christofides algorithm?

After constructing an MST and performing minimum weight matching, an Eulerian circuit is created, where each vertex is visited an even number of times. This allows the algorithm to convert the circuit into a Hamiltonian cycle by skipping repeated vertices.

Q7- What are the key steps in converting a Eulerian circuit to a Hamiltonian cycle in the Christofides algorithm?

In a Eulerian circuit, some cities might be visited more than once. To convert this into a Hamiltonian cycle, the algorithm skips repeated cities, ensuring each is visited exactly once.

Q8- Why is the Christofides algorithm popular in logistics and transportation planning?

Christofides provides near-optimal solutions quickly, making it practical for real-world applications like vehicle routing and delivery services where exact solutions are often unnecessary but speed and cost-efficiency are critical.

Q9- What is the time complexity of the Christofides algorithm?
  1. O(V²)
  2. O(V² log V)
  3. O(V log V)
  4. O(V!)

Ans – (2)

Explanation – The Christofides algorithm involves constructing a Minimum Spanning Tree (O(E log V)) and a minimum weight matching (O(V²)), leading to a time complexity of O(V² log V).

Q10- Which of the following is NOT a method for solving TSP?
  1. Brute Force
  2. Greedy Algorithms
  3. Dynamic Programming
  4. Dijkstra’s Algorithm

Ans – (4)

Explanation – Dijkstra’s algorithm is used for finding the shortest path in a graph, not for solving the TSP.

Q11- The Christofides algorithm guarantees a solution within what factor of the optimal cost?
  1. 1.25
  2. 1.5
  3. 2
  4. 2.5

Ans – (2)

Explanation – Christofides guarantees that the solution will be within 1.5 times the optimal solution for metric TSP.

Q12- What property of metric spaces is crucial for the Christofides algorithm?
  1. Symmetry
  2. Transitivity
  3. Triangle Inequality
  4. Reflexivity

Ans – (3)

Explanation – The triangle inequality is essential as it ensures that the direct path between two cities is never longer than a detour through an intermediate city.

The triangle inequality is a mathematical principle that applies to distances in metric spaces. It states that for any three points A, B, and C, the direct distance between two points is always shorter or equal to the sum of the distances through an intermediate point. In formula form, it is expressed as:

d(A,C) ≤ d(A,B) + d(B,C)

BOOKS

Algorithm T H CoremanAlgorithm by Udit AgarwalAlgorithm Ellis HorowitzData Structure & Algorithm Made Easy Narasimha

 

MCQs of Algorithm
GATE Syllabus
GATE Previous Year Paper