Catalan Number in Matrix Chain Multiplication

Catalan Number

.

The Catalan number plays a significant role in the Matrix Chain Multiplication problem, particularly when discussing the number of ways to parenthesize a product of matrices.

.

Catalan numbers are a sequence of natural numbers that have many applications in combinatorial mathematics. They appear in various counting problems, often involving recursive structures.

.

History

The sequence of numbers was named after the Belgian mathematician Eugène Charles Catalan (1814 – 1894), who first introduced them in the 19th century. Catalan’s work focused on counting the number of ways to divide polygons into triangles, which is a classic example of a problem involving Catalan numbers.

Catalan first described the sequence while studying various combinatorial problems, including the number of rooted binary trees and the number of ways to parenthesize products. His work included defining the numbers and providing their combinatorial interpretations.

The nth Catalan number can be found using the formula

.

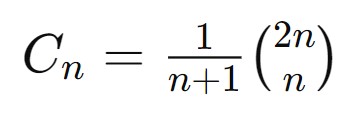
Or equivalently:

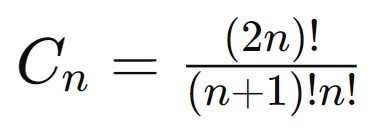
Here are the first few Catalan numbers:

• C₀ = 1
• C₁ = 1
• C₂ = 2
• C₃ = 5
• C₄ = 14
• C₅ = 42

.

Applications of Catalan Numbers

1. Binary Trees – The number of binary trees with n nodes are a Catalan number.
2. Parenthesizations – The number of ways to correctly match parentheses in an expression with n pairs of parentheses is a Catalan number.
3. Lattice Paths – The number of paths along the edges of a grid that do not pass above the diagonal is a Catalan number.
4. Polygon Triangulation – The number of ways to divide a polygon with n+2 sides into triangles using non-crossing diagonals are a Catalan number.

Catalan numbers arise in many other areas, making them an important sequence in mathematics. It is also related to matrix chain multiplication, specifically in counting the number of ways to fully parenthesize a product of n+1 matrices.

.

1. Matrix Chain Multiplication Problem – The problem involves finding the most efficient way to parenthesize a product of matrices to minimize the number of scalar multiplications.
2. Catalan Numbers – Catalan numbers are a sequence of natural numbers that have found applications in various combinatorial mathematics problems. They appear in contexts such as counting the number of ways to correctly parenthesize expressions, counting the number of rooted binary trees with a given number of nodes, and more.

For example, with 3 matrices, there are 2 ways to parenthesize them, which corresponds to the 2nd Catalan number.

.

Working

To determine the number of ways to parenthesize the product of 7 matrices A1*A2*A3*A4*A5*A6*A7​, we need the 6th Catalan number, since we have 6 multiplication operations (which correspond to 6 ways of parenthesizing the chain of 7 matrices).

The 6th Catalan number C₆​ is calculated as follows –

C₆ = (2⋅6)! / (6+1)!6! = 12! / 7!6!

So,

C₆ ​= 132

Therefore, there are 132 different ways to parenthesize the product of 7 matrices.

.

Example of Parenthesizing

Here are a few examples of how you might parenthesize the product of 7 matrices

1. ((((A1A2)A3)A4)A5)A6)A7
2. (A1(A2(A3(A4(A5(A6A7))))))
3. (A1(A2((A3A4)(A5(A6A7)))))
4. (A1((A2A3)(A4(A5(A6A7)))))
5. ((A1A2)((A3A4)(A5(A6A7))))

These are just a few of the 132 possible ways to parenthesize the product. Each distinct parenthesizing corresponds to a different way to group the matrices for multiplication.

.

Time Complexity

For calculating Catalan numbers using dynamic programming, the time complexity is O(n²), where n is the index of the Catalan number you want to compute.

.

Space Complexity

For calculating Catalan numbers using dynamic programming, the space complexity is O(n), where n is the index of the Catalan number you want to compute.

.

Advantage

Efficient Calculation – Using dynamic programming to calculate Catalan numbers reduces the time complexity to O(n²), making it feasible to compute for reasonably large values of n compared to a naive recursive approach.

Precomputation – Once the Catalan numbers are computed up to a certain index, they can be reused to solve various combinatorial problems efficiently, without needing recalculation.

Combinatorial Insights – Catalan numbers provide solutions to many combinatorial problems, such as counting valid parentheses combinations or binary trees. Precomputing these numbers facilitates quick access to solutions for such problems.