Breadth First Search (BFS) Algorithm
.
Definition
- Breadth First Search (BFS) is an algorithm used for traversing or searching tree or graph data structures.
- BFS splits all the vertices into two categories – Visited and Unvisited.
- It starts (visit) from a selected source vertex and visits all neighbouring vertices of the source vertex first before moving on to the next level vertices.

- BFS traverse vertices in a level-by-level manner, ensuring that vertices closer to the source vertex are visited before those farther away.
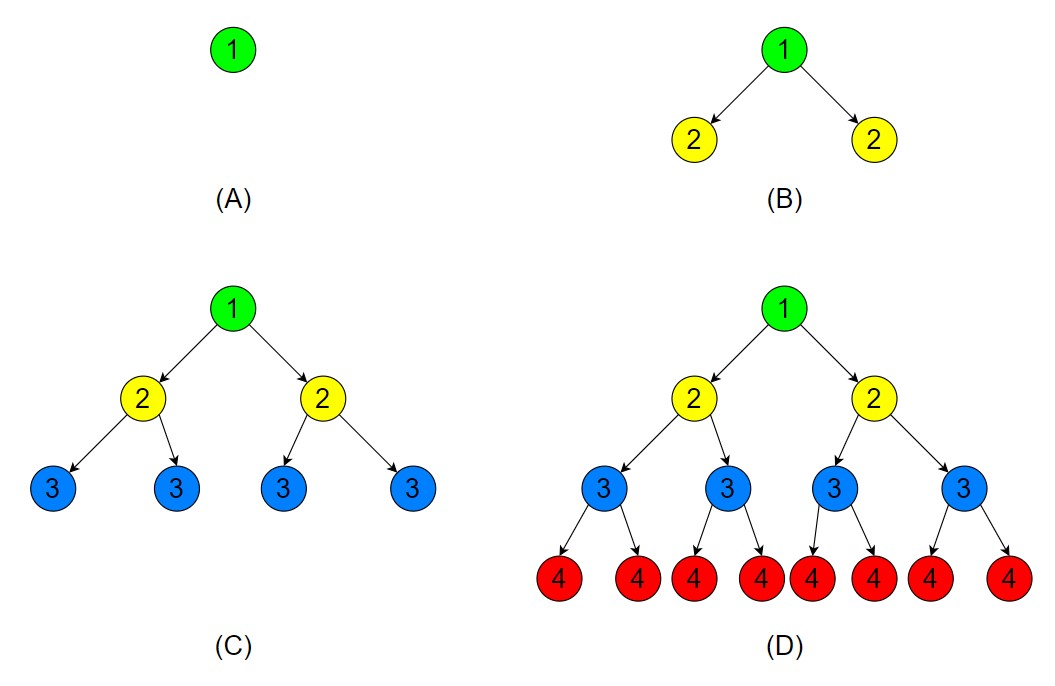
.
In diagram (A), we visited the source vertex or root vertex 1.
In diagram (B), we visited all the neighbouring vertices of source node numbered 1.
In diagram (C), we visited all the neighbouring vertices of nodes numbered 2.
In diagram (D), we visited all the neighbouring vertices of nodes numbered 3.
Note – Both the diagram represents the same Breadth First Search.
- It utilizes a queue data structure to keep track of the vertices to be visited next.
- BFS ensures that all vertices reachable from the source vertex are visited and processed.
.
Imagine you’re in a maze, and you want to find the shortest path from your starting point to the exit. With BFS, you would explore all the paths at the current layer before moving to the next layer. This means you’d first explore all adjacent nodes, then their adjacent nodes, and so on, until you find the exit or the destination.
Konrad Zuse developed Breadth First Search (BFS) Algorithm and used for locating related components of graphs in 1945, but his (rejected) Ph.D. thesis on the Plankalkül programming language was not published until 1972.
Edward F. Moore recreated it in 1959 and used it to determine the shortest path out of a maze.
C. Y. Lee then developed it into a wire routing method, which was published in 1961.
.
Algorithm of Breadth First Search (BFS)
Input – Graph G and starting vertex A
Output – Visited vertices in BFS order
Input – Graph G and starting vertex A | ||
Output – Visited vertices in BFS order | ||
1. | Create an empty queue Q. | |
2. | Enqueue the starting vertex s into Q and mark it as visited and change the color from white to grey. | |
3. | While Q is not empty – | |
1. | Dequeue a vertex u from Q. | |
2. | Visit and process vertex u. | |
3. | For each unvisited neighbour v of u | |
· Enqueue v into Q. | ||
· Mark v as visited & change color to grey. | ||
· Change color of u to black. | ||
4. | Repeat steps 3 until Q becomes empty. | |
.
Example
Consider a simple graph with nodes A, B, C, D, E, F, G, H.
Starting from node A, BFS would explore nodes layer by layer.
White – Indicates the vertex has not been visited.
Grey – Indicates the vertex is currently being visited.
Black – Indicates the vertex and all its neighbours have been visited.
Step 1 – Enqueue the starting vertex A into Q and mark it as visited and change the color from white to grey.
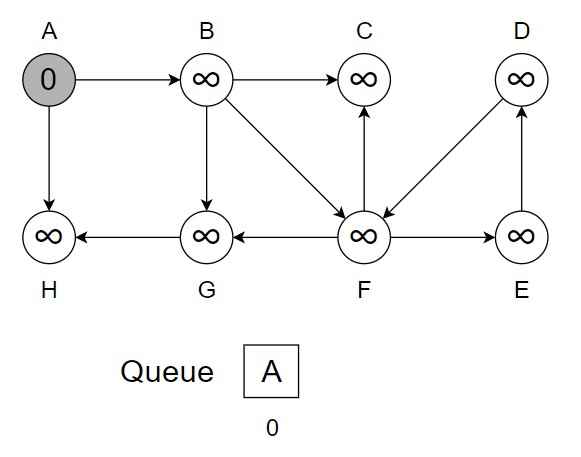
.
Step 2 – While Q is not empty – Dequeue vertex A from Q. Visit and process vertex A. For each unvisited neighbour {B, H} of A.
- Enqueue {B, H} into Q.
- Mark them as visited & change color to grey.
- Change color of A to black.
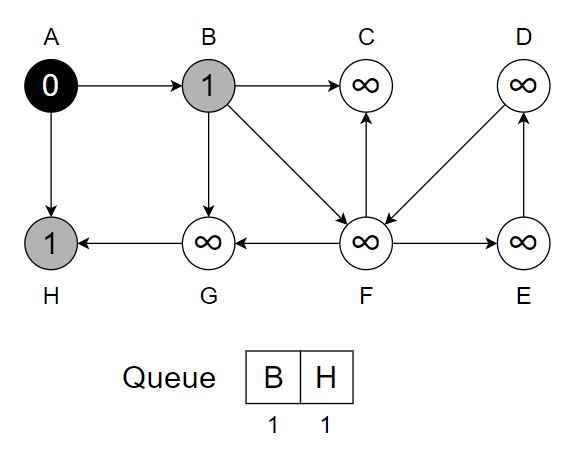
.
Step 3 – While Q is not empty – Dequeue vertex B from Q. Visit and process vertex B. For each unvisited neighbour {C, F, G} of A.
- Enqueue {C, F, G} into Q.
- Mark them as visited & change color to grey.
- Change color of B to black.
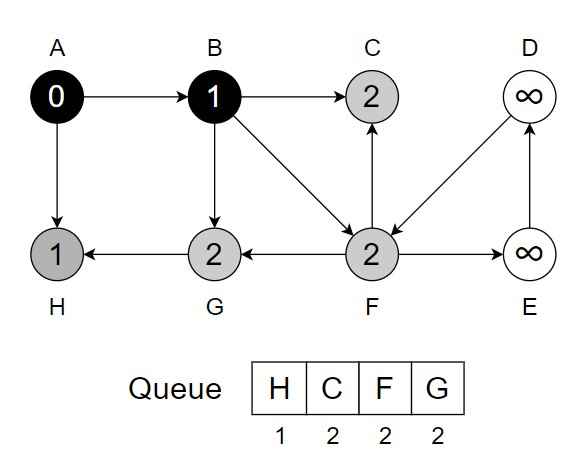
.
Step 4 – While Q is not empty – Dequeue vertex H from Q. Visit and process vertex H and it has no unvisited neighbour.
- Change color of H to black.
.
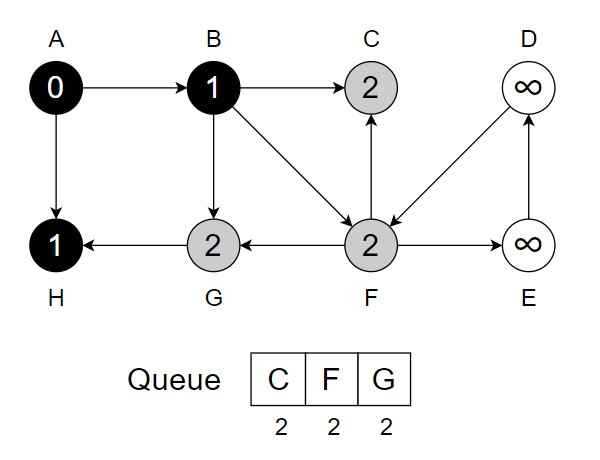
Step 5 – While Q is not empty – Dequeue vertex C from Q. Visit and process vertex C and it has no unvisited neighbour.
- Change color of C to black.
.
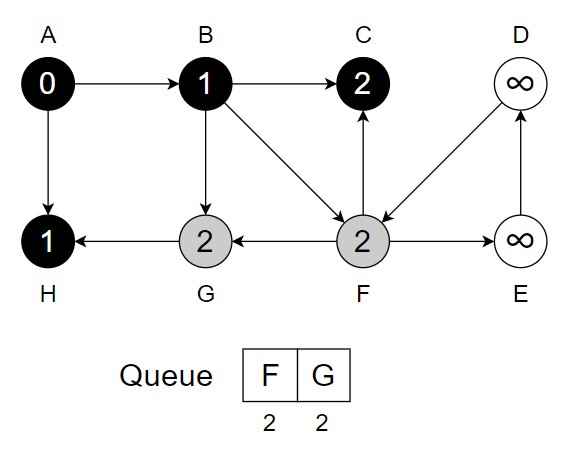
Step 6 – While Q is not empty – Dequeue vertex F from Q. Visit and process vertex F. For each unvisited neighbour {E, C, G} of F. C & G are already in the queue so neglect them.
- Enqueue {E} into Q.
- Mark it as visited & change color to grey.
- Change color of F to black.
.
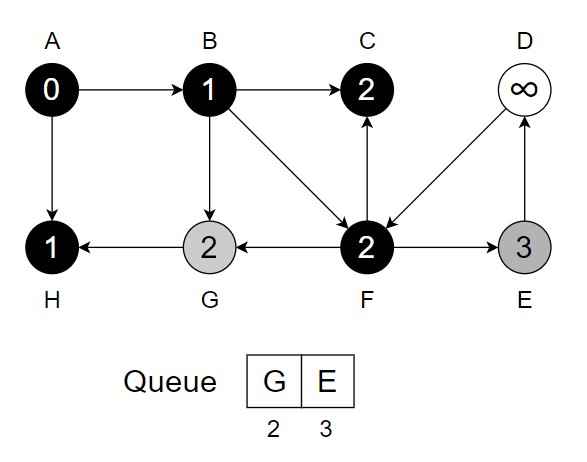
Step 7 – While Q is not empty – Dequeue vertex G from Q. Visit and process vertex G and it has no unvisited neighbour.
- Change color of G to black.
.
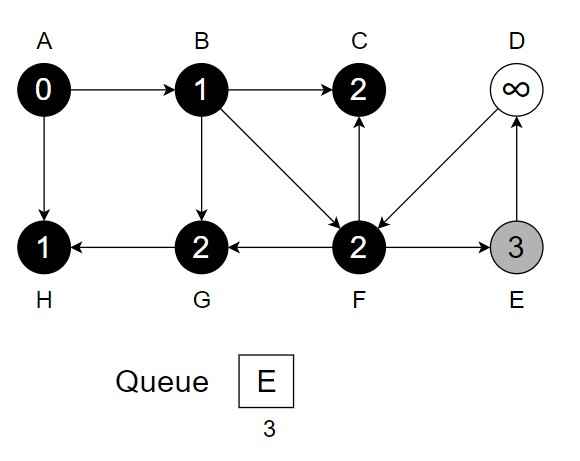
Step 8 – While Q is not empty – Dequeue vertex E from Q. Visit and process vertex E. For each unvisited neighbour {D} of E.
- Enqueue {D} into Q.
- Mark it as visited & change color to grey.
- Change color of E to black.
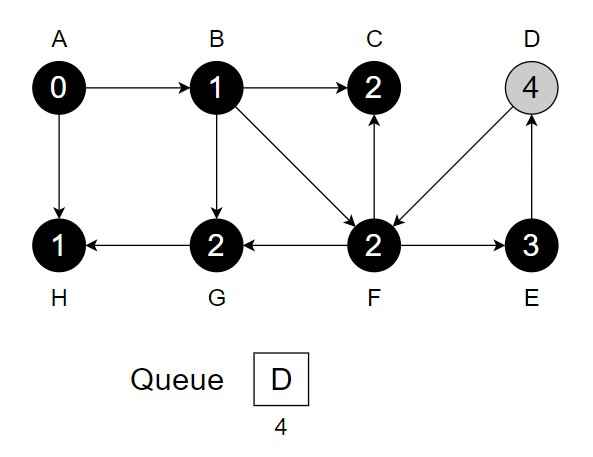
.
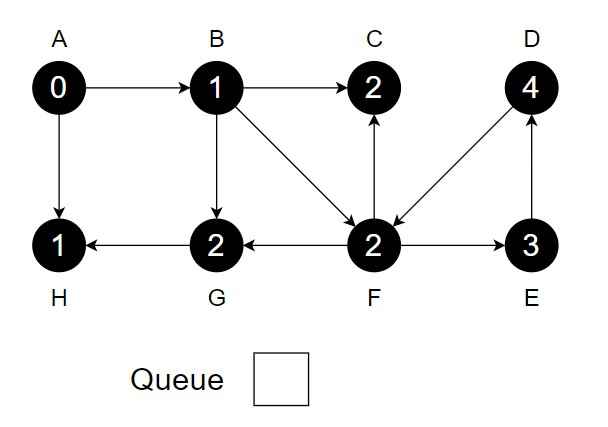
Step 9 – While Q is not empty – Dequeue vertex D from Q. Visit and process vertex D and it has no unvisited neighbour.
- Change color of D to black.
Source Code of Breadth First Search
// COMPUTER GEEK – compgeek.co.in
// Write a program for Breadth First Search
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX_VERTICES 100
// Queue implementation
typedef struct {
int items[MAX_VERTICES];
int front;
int rear;
} Queue;
Queue* createQueue() {
Queue* q = (Queue*)malloc(sizeof(Queue));
q->front = -1;
q->rear = -1;
return q;
}
bool isEmpty(Queue* q) {
return q->rear == -1;
}
void enqueue(Queue* q, int value) {
if (q->rear == MAX_VERTICES – 1) {
printf(“Queue is full.\n”);
return;
}
if (q->front == -1) {
q->front = 0;
}
q->rear++;
q->items[q->rear] = value;
}
int dequeue(Queue* q) {
int item;
if (isEmpty(q)) {
printf(“Queue is empty.\n”);
return -1;
} else {
item = q->items[q->front];
q->front++;
if (q->front > q->rear) {
q->front = q->rear = -1;
}
return item;
}
}
// Graph implementation
typedef struct {
int vertices[MAX_VERTICES][MAX_VERTICES];
int numVertices;
} Graph;
Graph* createGraph() {
Graph* graph = (Graph*)malloc(sizeof(Graph));
graph->numVertices = 0;
for (int i = 0; i < MAX_VERTICES; i++) {
for (int j = 0; j < MAX_VERTICES; j++) {
graph->vertices[i][j] = 0;
}
}
return graph;
}
void addEdge(Graph* graph, int src, int dest) {
graph->vertices[src][dest] = 1;
graph->vertices[dest][src] = 1; // For undirected graph
}
void BFS(Graph* graph, int startVertex) {
bool visited[MAX_VERTICES] = { false };
Queue* q = createQueue();
// Enqueue start vertex
enqueue(q, startVertex);
visited[startVertex] = true;
printf(“Visited vertex: %d\n”, startVertex);
while (!isEmpty(q)) {
int currentVertex = dequeue(q);
// Traverse adjacent vertices of currentVertex
for (int i = 0; i < graph->numVertices; i++) {
if (graph->vertices[currentVertex][i] == 1 && !visited[i]) {
enqueue(q, i);
visited[i] = true;
printf(“Visited vertex: %d\n”, i);
}
}
}
free(q);
}
int main() {
Graph* graph = createGraph();
int numVertices, numEdges;
printf(“Enter the number of vertices: “);
scanf(“%d”, &numVertices);
printf(“Enter the number of edges: “);
scanf(“%d”, &numEdges);
graph->numVertices = numVertices;
printf(“Enter the edges (in format: src dest):\n”);
for (int i = 0; i < numEdges; i++) {
int src, dest;
scanf(“%d %d”, &src, &dest);
addEdge(graph, src, dest);
}
int startVertex;
printf(“Enter the starting vertex for BFS: “);
scanf(“%d”, &startVertex);
printf(“BFS Traversal starting from vertex %d:\n”, startVertex);
BFS(graph, startVertex);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Breadth First Search
#include <iostream>
#include <queue>
#include <vector>
#include <unordered_set>
using namespace std;
class Graph {
private:
int numVertices;
vector<vector<int>> adjacencyList;
public:
Graph(int numVertices) : numVertices(numVertices) {
adjacencyList.resize(numVertices);
}
void addEdge(int src, int dest) {
adjacencyList[src].push_back(dest);
adjacencyList[dest].push_back(src); // For undirected graph
}
void BFS(int startVertex) {
vector<bool> visited(numVertices, false);
queue<int> q;
q.push(startVertex);
visited[startVertex] = true;
cout << “Visited vertex: ” << startVertex << endl;
while (!q.empty()) {
int currentVertex = q.front();
q.pop();
for (int neighbor : adjacencyList[currentVertex]) {
if (!visited[neighbor]) {
q.push(neighbor);
visited[neighbor] = true;
cout << “Visited vertex: ” << neighbor << endl;
}
}
}
}
};
int main() {
int numVertices, numEdges;
cout << “Enter the number of vertices: “;
cin >> numVertices;
Graph graph(numVertices);
cout << “Enter the number of edges: “;
cin >> numEdges;
cout << “Enter the edges (in format: src dest):\n”;
for (int i = 0; i < numEdges; ++i) {
int src, dest;
cin >> src >> dest;
graph.addEdge(src, dest);
}
int startVertex;
cout << “Enter the starting vertex for BFS: “;
cin >> startVertex;
cout << “BFS Traversal starting from vertex ” << startVertex << “:\n”;
graph.BFS(startVertex);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Breadth First Search
import java.util.*;
class Graph {
private int numVertices;
private List<List<Integer>> adjacencyList;
public Graph(int numVertices) {
this.numVertices = numVertices;
adjacencyList = new ArrayList<>(numVertices);
for (int i = 0; i < numVertices; ++i) {
adjacencyList.add(new ArrayList<>());
}
}
public void addEdge(int src, int dest) {
adjacencyList.get(src).add(dest);
adjacencyList.get(dest).add(src); // For undirected graph
}
public void BFS(int startVertex) {
boolean[] visited = new boolean[numVertices];
Queue<Integer> queue = new LinkedList<>();
queue.add(startVertex);
visited[startVertex] = true;
System.out.println(“Visited vertex: ” + startVertex);
while (!queue.isEmpty()) {
int currentVertex = queue.poll();
for (int neighbor : adjacencyList.get(currentVertex)) {
if (!visited[neighbor]) {
queue.add(neighbor);
visited[neighbor] = true;
System.out.println(“Visited vertex: ” + neighbor);
}
}
}
}
}
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print(“Enter the number of vertices: “);
int numVertices = scanner.nextInt();
Graph graph = new Graph(numVertices);
System.out.print(“Enter the number of edges: “);
int numEdges = scanner.nextInt();
System.out.println(“Enter the edges (in format: src dest):”);
for (int i = 0; i < numEdges; ++i) {
int src = scanner.nextInt();
int dest = scanner.nextInt();
graph.addEdge(src, dest);
}
System.out.print(“Enter the starting vertex for BFS: “);
int startVertex = scanner.nextInt();
System.out.println(“BFS Traversal starting from vertex ” + startVertex + “:”);
graph.BFS(startVertex);
scanner.close();
}
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Breadth First Search
from collections import deque
class Graph:
def __init__(self, num_vertices):
self.num_vertices = num_vertices
self.adjacency_list = [[] for _ in range(num_vertices)]
def add_edge(self, src, dest):
self.adjacency_list[src].append(dest)
self.adjacency_list[dest].append(src) # For undirected graph
def bfs(self, start_vertex):
visited = [False] * self.num_vertices
queue = deque()
queue.append(start_vertex)
visited[start_vertex] = True
print(f”Visited vertex: {start_vertex}”)
while queue:
current_vertex = queue.popleft()
for neighbor in self.adjacency_list[current_vertex]:
if not visited[neighbor]:
queue.append(neighbor)
visited[neighbor] = True
print(f”Visited vertex: {neighbor}”)
num_vertices = int(input(“Enter the number of vertices: “))
graph = Graph(num_vertices)
num_edges = int(input(“Enter the number of edges: “))
print(“Enter the edges (in format: src dest):”)
for _ in range(num_edges):
src, dest = map(int, input().split())
graph.add_edge(src, dest)
start_vertex = int(input(“Enter the starting vertex for BFS: “))
print(f”BFS Traversal starting from vertex {start_vertex}:”)
graph.bfs(start_vertex)
Enter the number of vertices: 8
Enter the number of edges: 11
Enter the edges (in format: src dest):
0 1
0 7
1 2
1 5
1 6
7 6
6 5
2 5
5 3
3 4
5 4
Enter the starting vertex for BFS: 0
BFS Traversal starting from vertex 0:
Visited vertex: 0
Visited vertex: 1
Visited vertex: 7
Visited vertex: 2
Visited vertex: 5
Visited vertex: 6
Visited vertex: 3
Visited vertex: 4
=== Code Execution Successful ===
Time Complexity
In the worst-case scenario, the time complexity of the Breadth First Search (BFS) algorithm is O(V + E), where V is the number of vertices and E is the number of edges in the graph.
In the worst case, each vertex is visited once, and each edge is traversed once.
Visiting a vertex and traversing an edge both take constant time, assuming that the graph is represented using an adjacency list or matrix.
.
Space Complexity
The space complexity of BFS is O(V), where V is the number of vertices. This is because it requires additional queue to store the visited nodes and the queue.
.
Advantages
- It exhaustively explores all vertices at each level of the graph, ensuring that no vertices are missed.
- It typically uses a queue data structure to maintain the order of vertices to be visited.
- It does not use recursion, making it less prone to stack overflow errors.
- It guarantees finding the shortest path between the starting vertex and any other reachable vertex in an unweighted graph.
.
Disadvantages
- Requires more memory as it stores all visited nodes.
- Inefficient for large graphs or graphs with complex structures.
- In weighted graphs, where edges have different weights or costs, BFS may not find the shortest path due to its greedy nature.
.
Applications
- Shortest path finding
- Web crawling
- Social network analysis
- Minimum spanning tree algorithms
- Solving puzzles like the 15-puzzle
- Finding connected components in an undirected graph
- Network flow analysis
- Bipartite graph detection
- Wireless sensor network routing
- Maze solving
- Level-order traversal of trees
- Analyzing and optimizing game states in artificial intelligence
Test Yourself
Q1- Can BFS find the shortest path in a weighted graph? Why or why not?
No, BFS cannot find the shortest path in a weighted graph because it assumes all edges have the same weight. In a weighted graph, where edges have different weights or costs, BFS may not find the optimal path.
Q2- Is BFS more memory-efficient than DFS? Explain.
In general, BFS requires more memory than DFS because it stores all the visited vertices in a queue. However, in certain scenarios or graph structures, DFS may require more memory due to its recursive nature and deep call stack.
Q3- Can BFS be used to detect cycles in a graph?
No, BFS alone cannot be used to detect cycles in a graph because it does not maintain information about back edges. However, BFS can be combined with other algorithms or techniques to detect cycles in a graph efficiently.
Q4- Explain the Breadth First Search (BFS) algorithm and its working principle.
Breadth First Search (BFS) is an algorithm used for traversing or searching tree or graph data structures. It starts from a selected source vertex and visits all neighboring vertices of the source vertex first before moving on to the next level vertices.
Q5- Explain how BFS can be used for web crawling.
BFS can be used for web crawling by treating web pages as vertices and hyperlinks as edges. It starts from a seed URL, visits all linked pages at the same level, and then moves to the next level, ensuring a systematic and comprehensive exploration of the web.
Q6- Describe the steps involved in implementing BFS using a queue data structure.
The steps involve initializing a queue, enqueueing the starting vertex, dequeuing vertices, visiting and processing each vertex, and enqueuing its unvisited neighbours.
Q7- How does BFS ensure completeness in traversing a graph?
BFS ensures completeness by systematically exploring all vertices reachable from the starting vertex, ensuring that no vertices are missed during traversal.
Q8- What is the time complexity of Breadth First Search (BFS) in terms of vertices (V) and edges (E)?
1. O(V)
2. O(E)
3. O(V + E)
4. O(V * E)
Ans – (3)
Explanation – BFS traverses each vertex and edge once, leading to a time complexity of O(V + E).
Q9- Which data structure is commonly used in BFS for maintaining the order of vertices to be visited?
1. Stack
2. Heap
3. Queue
4. Set
Ans – (3)
Q10- Which property of BFS guarantees finding the shortest path in unweighted graphs?
1. Completeness
2. Optimality
3. Memory Efficiency
4. Scalability
Ans – (2)
Q11- What is the space complexity of BFS in terms of the number of vertices (V)?
1. O(1)
2. O(V)
3. O(V + E)
4. O(V * E)
Ans – (2)
Q12- Which step is NOT involved in the BFS algorithm?
1. Enqueuing the starting vertex
2. Dequeuing a vertex
3. Marking vertices as processed
4. Popping a vertex from the stack
Ans – (4)
Explanation – Stack is not used in the BFS. Queue is used.






