Boolean Satisfiability Problem (SAT)

Introduction

.

The Boolean Satisfiability Problem (SAT) is one of the most important problems in computer science. It asks whether a given Boolean formula can be made true by assigning truth values (true or false) to its variables. SAT was the first problem to be proven NP-complete.

.

What is SAT?

The Boolean Satisfiability Problem asks whether there is a way to assign truth values (true or false) to variables in a Boolean formula, so that the entire formula evaluates to true.

A Boolean formula is built using

• Variables (e.g., x1, x2, …)
• Logical operators like AND ( ∧ ), OR ( ∨ ), and NOT ( ¬ ).

For example, a SAT problem could be

(x1 ∨ x2) ∧ (¬x2 ∨ x3)

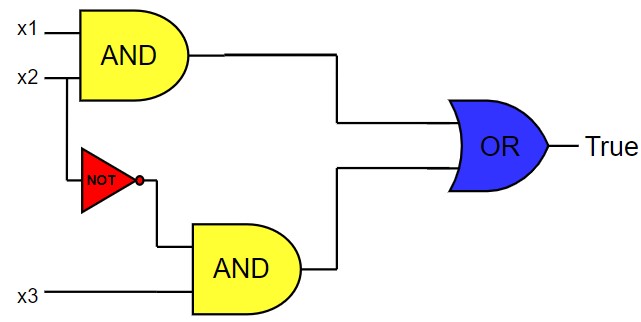
The question is that can we assign values to x1, x2, x3 such that this formula evaluates to true?

If there exists such an assignment, the formula is said to be satisfiable. If no such assignment exists, the formula is unsatisfiable.

.

The Discovery of NP-Complete Problems

The breakthrough came in 1971, when American computer scientist Stephen Cook made a revolutionary discovery. He introduced the concept of NP-completeness in his paper “The Complexity of Theorem-Proving Procedures.”

Cook identified a set of problems that were the hardest problems in NP. These problems are called NP-complete problems. If you could find a fast (polynomial-time) solution for any one NP-complete problem, you could solve all NP problems quickly.

.

Boolean Satisfiability Problem is NP-Complete

Cook’s most famous result was showing that the Boolean Satisfiability Problem (SAT) is NP-complete. This means:

1. SAT belongs to NP.
2. Every other problem in NP can be reduced to SAT in polynomial time.

This makes SAT the first NP-complete problem, and it opened the door to a vast new field of research on NP-completeness.

Cook’s theorem, called the Cook-Levin Theorem, proves that any problem in NP can be transformed into an instance of SAT in polynomial time. This means that if we could find a fast algorithm to solve SAT, we could also solve every other NP-complete problem quickly.

.

Variants of SAT

Variants of SAT, such as 2-SAT and 3-SAT, are based on the number of literals in each clause. Additionally, the terms 2-CNF and 3-CNF refer to specific forms of SAT where the formula is in Conjunctive Normal Form (CNF), meaning it consists of a conjunction of clauses, and each clause is a disjunction of literals.

.

Conjunctive Normal Form (CNF) or Product of Sums (POS)

CNF is a way of structuring a Boolean formula. A formula in CNF is a conjunction (AND) of one or more clauses, where each clause is a disjunction (OR) of literals. A literal is either a variable or its negation.

For example, the formula

(x1 ​∨ ¬x2​) ∧ (x1 ​∨ ¬x3​)

is in CNF or POS because it is an AND of two clauses, and each clause is an OR of literals.

A Boolean formula is in 2-CNF if each clause has exactly two literals. For example, (x1​ ∨ ¬x2​) ∧ (x2 ​∨ x3​) is a 2-CNF formula.

A Boolean formula is in 3-CNF if each clause has exactly three literals. For example, (x1 ​∨ ¬x2 ​∨ x3​) ∧ (¬x1 ​∨ x2​∨ ¬x3​) is a 3-CNF formula.

.

Working of SAT

A Boolean formula consists of variables and logical operators like AND ( ∧ ), OR ( ∨ ), and NOT ( ¬ ). The goal of the SAT problem is to determine if there is a way to assign true or false values to the variables such that the formula evaluates to true.

.

SAT Algorithm (Brute Force Approach)

A simple way to solve SAT is by brute force, where all possible combinations of truth values are tried for the variables to check if the formula evaluates to true.

1. Input – A Boolean formula in CNF with variables.
2. For each possible assignment of truth values to the variables:
3. Substitute the truth values into the formula.
4. Evaluate the formula.
5. If the formula evaluates to true, return “Satisfiable“.
6. If no truth assignment satisfies the formula, return “Unsatisfiable“.

.

2-SAT Problem

2-SAT is a special case where the Boolean formula is in 2-CNF, meaning each clause has exactly two literals. 2-SAT can be solved in polynomial time. It is easier to solve than general SAT or 3-SAT problems, which are NP-complete.

(x1​ ∨ ¬x2​) ∧ (¬x1 ​∨ x3​)

This formula can be solved efficiently using graph-based algorithms such as Kosaraju’s Algorithm for strongly connected components.

.

Algorithm for 2-SAT

1. Convert each clause into two implications.
   • For (x1 ∨ ¬x2), If x2 is true, then x1​ must be true. If x1 is false, then x2​ must be false.
2. Build the implication graph.
3. Find strongly connected components using Kosaraju’s Algorithm.
4. If no variable and its negation appear in the same strongly connected component, the formula is satisfiable.

.

Example of a 2-SAT problem

(x1 ​∨ ¬x2​) ∧ (¬x1​ ∨ x3​)

1. We have three variables – x1, x2, x3​.
2. Possible assignments of truth values are {T, F} (True or False).

For x1 = True, x2 = True, x3 = True, the formula becomes True. Therefore, this formula is satisfiable.

.

3-SAT Problem

3-SAT is a more complex variant where the formula is in 3-CNF, and each clause has exactly three literals. Unlike 2-SAT, 3-SAT is NP-complete, meaning it is computationally hard to solve.

(x1 ​∨ ¬x2​ ∨ x3​) ∧ (¬x1​ ∨ x2 ​∨ ¬x3​)

Since 3-SAT is NP-complete, there is no known polynomial-time algorithm to solve it. We cannot solve it as an implication graph. It is generally solved using brute force, backtracking, or the DPLL (Davis–Putnam–Logemann–Loveland) algorithm.

.

Algorithm for 3-SAT

1. Try all possible truth assignments for the variables.
2. Evaluate the formula for each combination.
3. If a combination satisfies the formula, the formula is satisfiable; otherwise, it is unsatisfiable.

.

Example of a 3-SAT formula

(x1 ∨ ¬x2 ∨ x3) ∧ (¬x1 ∨ x2 ∨ ¬x4)

x1​=True, x2​=True, x3​=False, x4​=False. Since all the two clauses are true, the formula is satisfiable for this truth assignment.

For small problems (like the example with only 4 variables), you can easily try different combinations of truth values to find a satisfying assignment.

However, if the number of variables becomes large, the number of possible assignments grows exponentially.

So, if n=10, there are 2¹⁰ = 1024 assignments to check. For n=100, there are 2¹⁰⁰, which is more than 1 trillion possible combinations!

.

Q – If we produce 100 variables in 2-SAT problem than 2-SAT is also np complete?

Answer – 2-SAT can be represented as an implication graph where each clause corresponds to two implications. Using graph algorithms like Tarjan’s algorithm or Kosaraju’s algorithm, we can efficiently find strongly connected components (SCCs) in the implication graph.

(x1​ ∨ ¬x2​) ∧ (¬x3​ ∨ x4​) ∧ (¬x1 ​∨ x2​)

• (x1​ ∨ ¬x2​) becomes ¬x1 → x2 and x2 → ¬x1​
• (¬x3 ∨ x4) becomes x3 → x4 and ¬x4 ​→ x3​
• (¬x1 ∨ x2) becomes x1 → x2​ and ¬x2 → ¬x1

Using an SCC algorithm, we can check whether the formula is satisfiable in linear time. Even if you have 100 variables in a 2-SAT problem, it can still be solved in polynomial time.