Binomial Heap

Binomial Heap is a group of binomial trees

.

Binomial Tree

A binomial tree is an ordered tree, and it is denoted by B_k where k is the degree of the root.

It has some properties which is –

1. B_k tree has 2^k nodes.
2. Degree of root is k. it means the root have k children. All the other nodes who are present in the tree have a degree less than k.
3. Height of the tree is also k.
4. There are exactly ^kC_i nodes at depth i, where ^kC_i = (k!) / (k-i)! i!
5. The binomial tree B_k has two B_k-1 trees. Alternatively, we can say that 2^k-1 + 2^k-1 trees will form a 2^k tree.

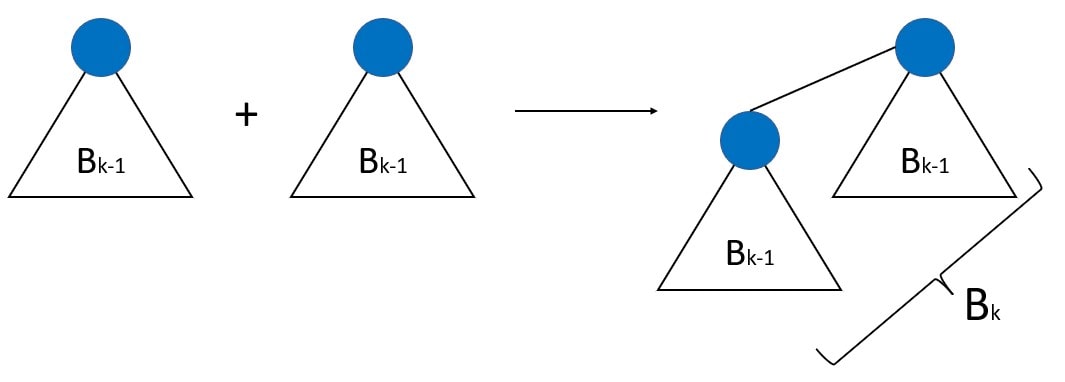
The binomial tree examples are

B0
B1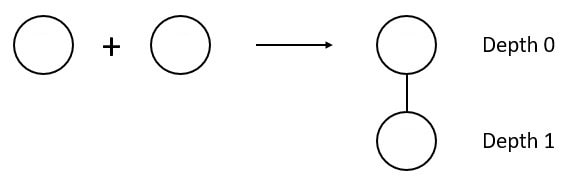
B2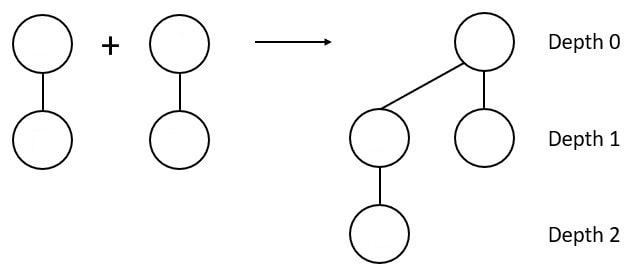
B3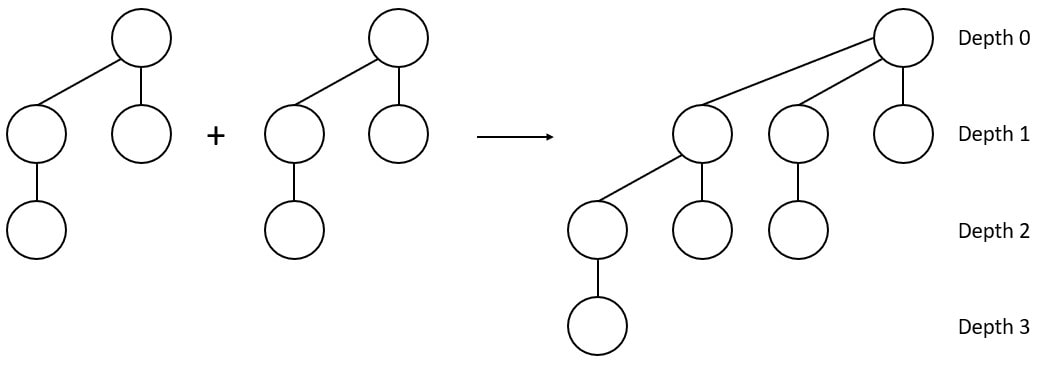

Binomial Heap

A binomial heap is constructed as a recursively defined set of binomial trees. It was introduced by Jean Vuillemin in 1978.

The binomial trees must satisfy the certain properties.

The properties are –

1. The min heap rule is maintained by each binomial tree.

2. All binomial trees are connected through by a linked list.

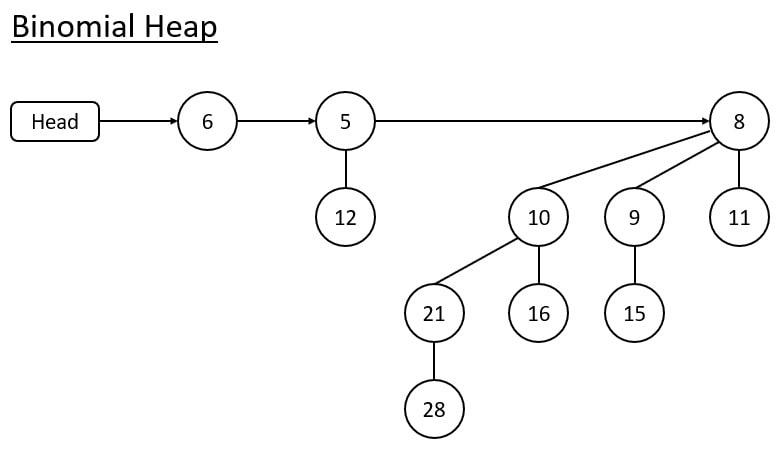
In the above diagram, there is a binomial heap. All the binomial trees are connected through a linked list, and every heap obeys the min-heap property.

We can quickly identify the binomial trees that will be present in a heap if we know how many nodes it contains by looking at the binary representation.

Number of nodes = 1 in B₀ + 2 in B₁ + 8 in B₃ = 11

The binary representation of 11 is 1011

So, the binomial heap contains the binomial trees B₀, B₁ and B₃.

So, 1*2³ + 0*2² + 1*2¹ + 1*2⁰ = 11

Operations in Binomial Heap

1. Make a heap
2. Insertion
3. Merging two heap
4. Find the minimum key
5. Extracting the minimum key
6. Decreasing a key
7. Deleting a key

1. Make a heap

Place a head and make an arrangement of linked lists so that every node after inserting will follow the links.

Because there is no node in the binomial tree, Head[link] = NIL.

This is a very simple process with a time complexity of Ɵ(1).

.

2. Insertion

If we wish to insert a node to create a binomial heap, we must follow several rules that are specific to binomial heaps.

Rule 1 – There is a head variable at the start, and all the binomial trees are connected by the root through a linked list.

Rule 2 – Each inserted node will form a separate binomial tree, and we will consider it the root of the tree that is connected to the linked list.

Rule 3 – No two binomial trees can contain the same k. They have to follow the merge operation that is discussed later.

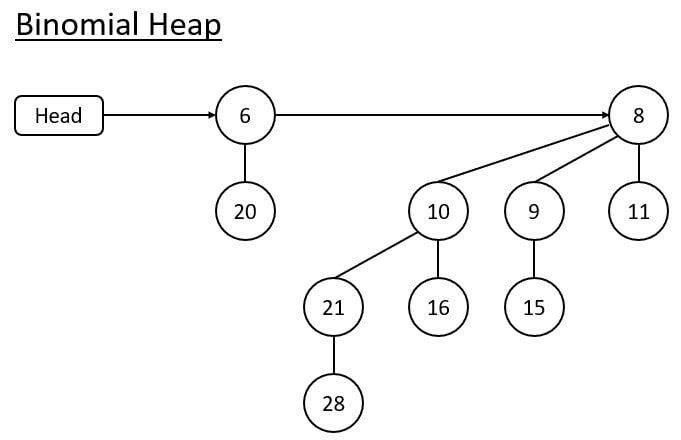
Suppose we want to insert 12 in the binomial heap. Then we have to insert 12 as a separate binomial tree, B₀.

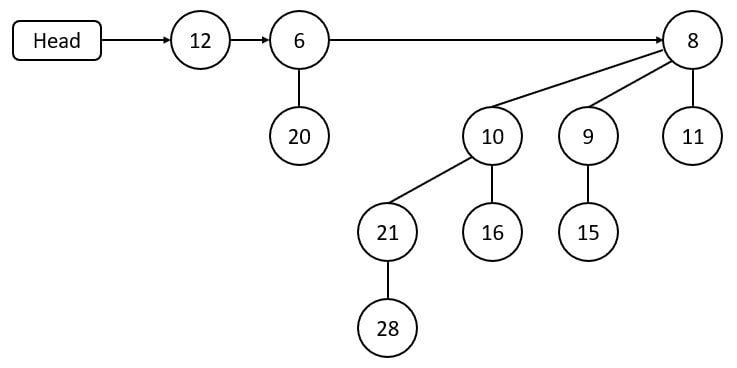
Time Complexity of inserting is O(log n).

.

3. Merging two Heaps

By doing some operation (inserting or deleting) in the binomial heap, if the result is that there are two binomial trees that have the same degree k, then a merge operation is applied to the two trees.

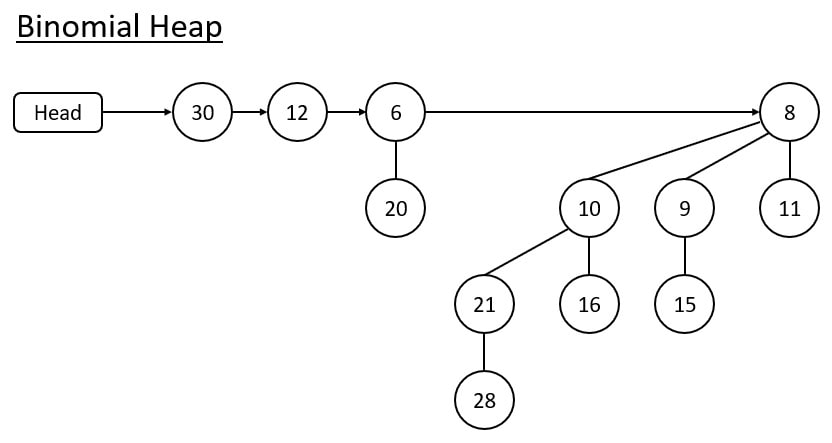
In the above diagram, there are two binomial trees whose degree is the same, 30 and 12.

Choose the smaller value as the new root and the larger value as the smaller value’s child.

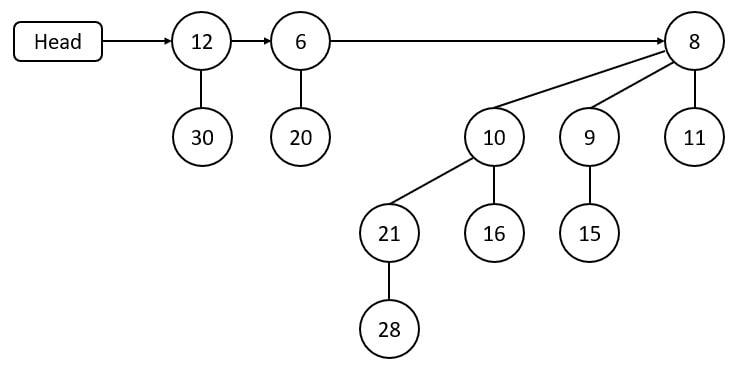
There are now two binomial trees with the same degree.

Merge them with the smaller value of the root to create a new root, and the larger value of the root becomes a child of the smaller value.

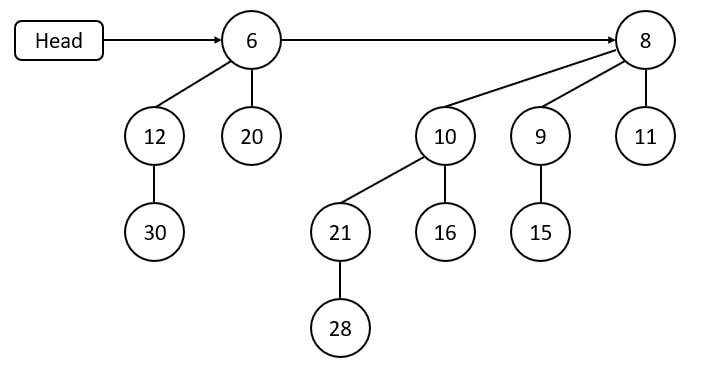
Time complexity of merging two binomial heaps is O(log n).

.

4. Find the minimum key

Every binomial heap has a min-heap property. As a result, the root has the smallest element. To discover the minimum key, we must search all of the roots. 6 has the least value of the root nodes 17, 6, and 8.

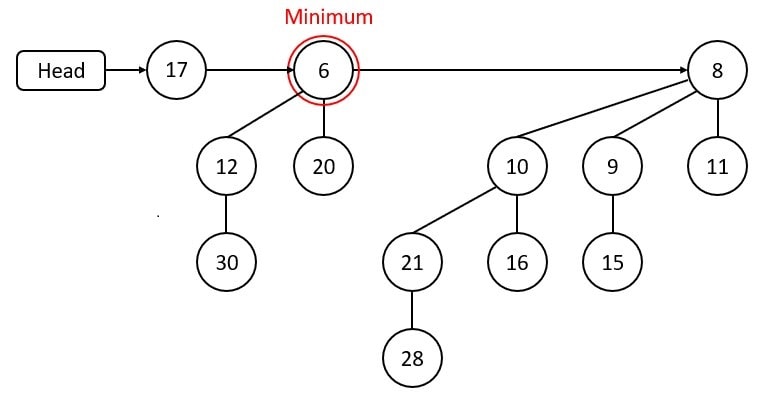
Time complexity of finding the minimum key is O(log n).

.

5. Extracting the minimum key

It means removing the minimum key of the binomial heap. In the diagram for finding the minimum key, node 6 is identified as the minimum key.

After extracting or removing node 6, the orphaned subtrees that arise are added back to the heap as independent trees.

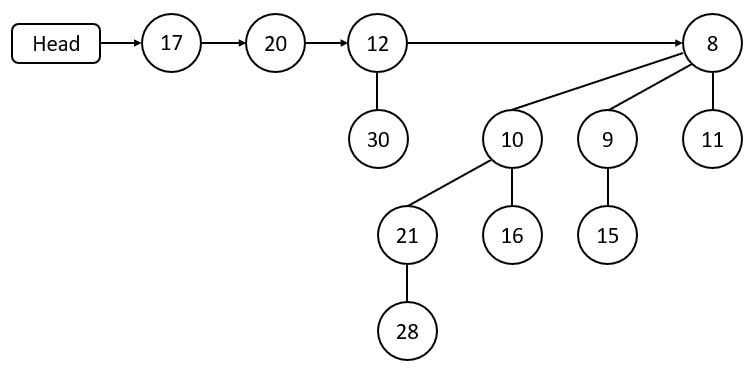
This is the result of removing node 6. Node 12 and node 20 become root.

This binomial heap is not perfect, as node 17 and node 20 belong to the same degree. So, a merging operation is performed to get it in perfect shape. After that, there are two trees of the same degree 1. Therefore, a second merging operation is required, and the resultant binomial heap is

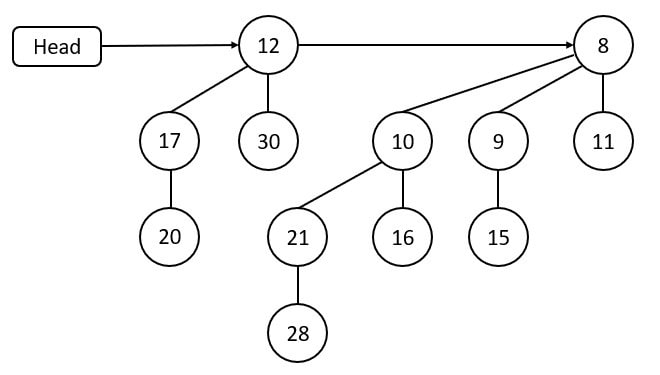
Time complexity of extracting the minimum key is O(log n).

.

6. Decreasing a key

The min-heap property may be lost if an element’s key decreases to the point where it is smaller than the value of its parent. Change the element’s parent, possibly its grandparent, and so on until the min-heap property is no longer violated.

If 28 is decreased by 9,

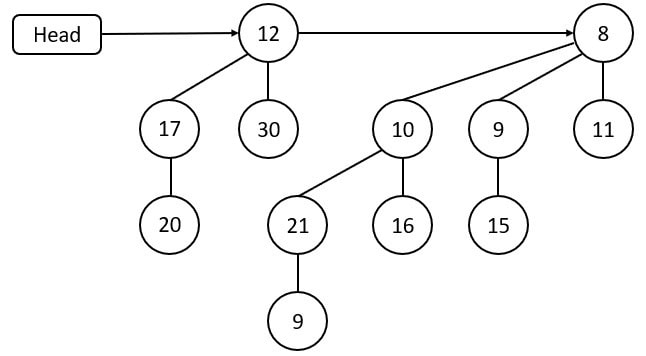
Then node 9 is replaced by its grandparent node 10 to not violate the min-heap property. Its parent node 21 replaces node 9, and grandparent node 10 replaces node 21.

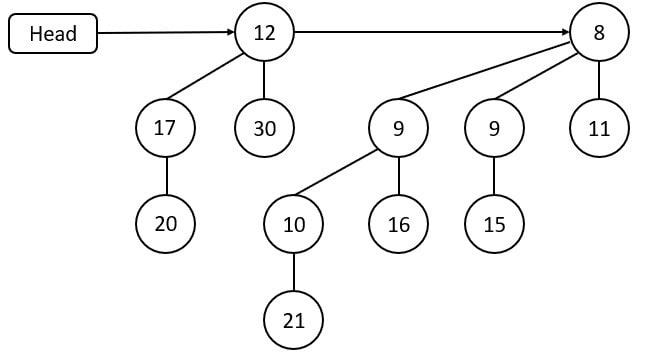
Time complexity of decreasing a key is O(log n).

.

7. Deleting a key

In the other data structures, deleting a key replaces it with its predecessor or successor, but in the binomial heap, it is not so simple. It deletes the node by setting its value to (-∞) negative infinity.

Suppose if we want to delete node 20, first replace it with (-∞).

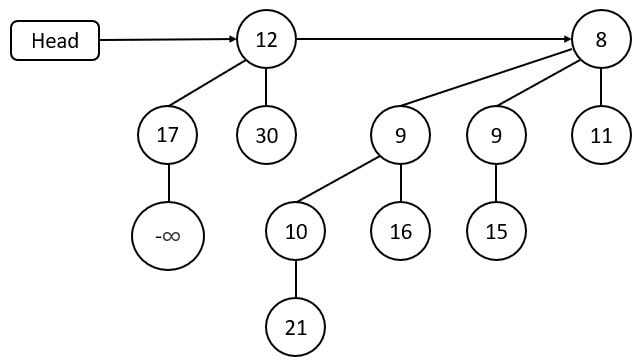
To satisfy the min-heap property, (-∞) is taken to the root.

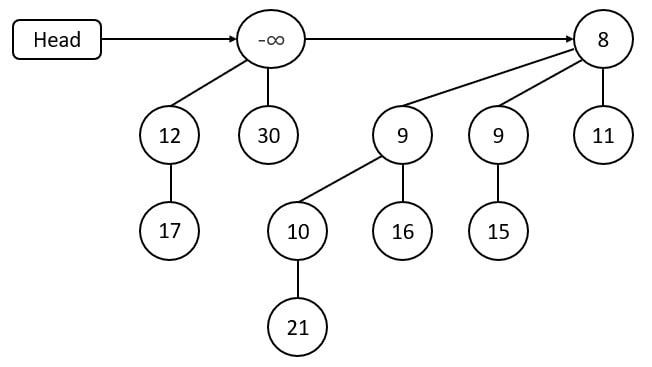
Remove (-∞). The orphaned subtrees that arise are added back to the heap as independent trees.

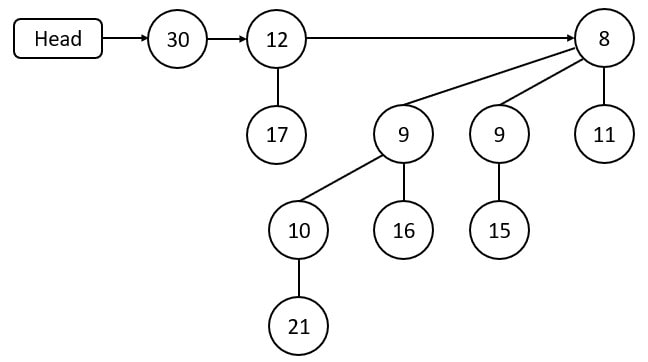
Time complexity of deleting a key or node is O(log n).

Space complexity is O(n).

.

Application

1. A data structure that functions as a priority queue is the binomial heap.
2. Memory management systems make use of heaps to effectively create and deallocate memory blocks of various sizes.
3. Binomial heaps can be used in parallel computing applications, where numerous threads or processes must access and alter shared data structures simultaneously.